CompChem2:mc4716
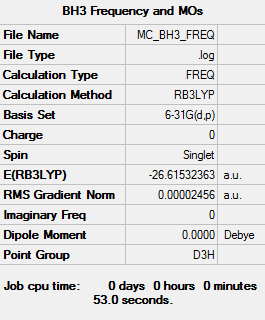
BH3
B3LYP/6-31G(d,p)
Item Value Threshold Converged? Maximum Force 0.000049 0.000450 YES RMS Force 0.000025 0.000300 YES Maximum Displacement 0.000193 0.001800 YES RMS Displacement 0.000097 0.001200 YES
Frequency file: MC_BH3_FREQ.LOG
Low frequencies --- -0.2279 -0.0080 0.0005 22.0037 22.0049 24.0346 Low frequencies --- 1163.1731 1213.2725 1213.2727
optimised BH3 molecule |
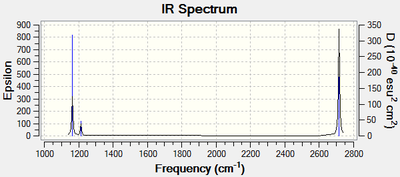
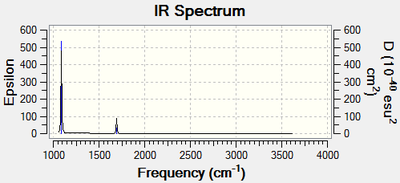
Vibrational spectrum for BH3
| Wavenumber (cm-1) | Intensity (arbitrary units) | Symmetry | IR active? | Type |
| 1163 | 92 | A1 | yes | out-of-plane bend |
| 1213 | 14 | E | very slight | bend |
| 1213 | 14 | E | very slight | bend |
| 2581 | 0 | A1 | no | symmetric stretch |
| 2714 | 126 | E | yes | asymmetric stretch |
| 2714 | 126 | E | yes | asymmetric stretch |
|
It is known that there will be 3n-6 vibrational frequencies. Therefore BH3 will have 6 vibrational frequencies, yet only 3 peaks are present in the spectrum above. This is due to two factors. The first is that one of the vibrational modes, the symmetric stretch, is IR inactive. The second is that there are two sets of two modes that are degenerate meaning where there are four distinct modes, there are only two distinct frequency peaks seen in the spectrum. So in review, two modes are degenerate to other modes and one is IR inactive, leaving the 3 distinct peaks that can be seen.
Smf115 (talk) 17:49, 23 May 2018 (BST)Great explaination to why only 3 peaks are seen and assignment of the vibraitonal modes. The symmetries assigned weren't correct though suggesting that the molecule was of the wrong point group.
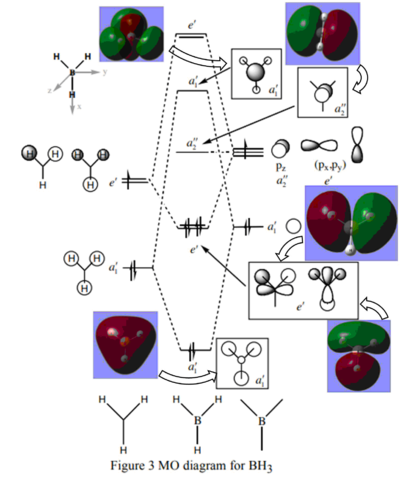
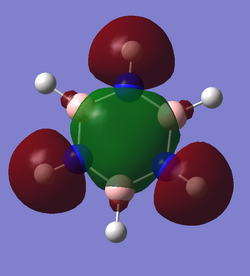
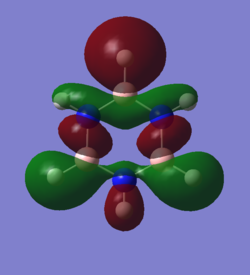
Molecular Orbitals for BH3
Diagram provided by Dr.Hunt, teaching notes, page 2 PDF Teaching Notes
The main differences between the calculated and LCAO molecular orbitals is that in the calculated orbitals the overlap of like regions is represented and the quantitative size of the orbitals is estimated. These properties of the calculated orbitals make them much more representative of the natural orbitals and therefore are more useful in predicting the real behavior of the natural compounds as the distance and location of interactions can more accurately be predicted.
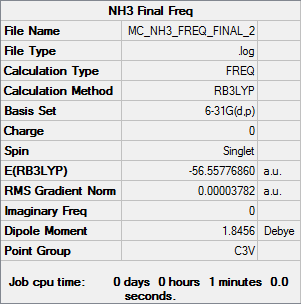
NH3
B3LYP/6-31G(d,p)
Item Value Threshold Converged? Maximum Force 0.000049 0.000450 YES RMS Force 0.000025 0.000300 YES Maximum Displacement 0.000193 0.001800 YES RMS Displacement 0.000097 0.001200 YES
Frequency file: MC_NH3_FREQ.LOG
Low frequencies --- -30.9305 -30.9169 -0.0036 0.0078 0.0258 3.3190 Low frequencies --- 1088.6130 1694.0221 1694.0224
optimised NH3 molecule |
Vibrational spectrum for NH3
| Wavenumber (cm-1) | Intensity (arbitrary units) | Symmetry | IR active? | Type |
| 1088 | 145 | A1 | yes | out-of-plane bend |
| 1694 | 13 | E | very slight | bend |
| 1694 | 13 | E | very slight | bend |
| 3461 | 1 | A1 | no | symmetric stretch |
| 3590 | 0 | E | no | asymmetric stretch |
| 3590 | 0 | E | no | asymmetric stretch |
|
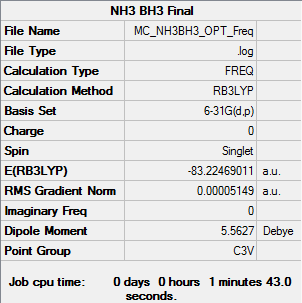
NH3BH3
B3LYP/6-31G(d,p)
Item Value Threshold Converged? Maximum Force 0.000230 0.000450 YES RMS Force 0.000051 0.000300 YES Maximum Displacement 0.001358 0.001800 YES RMS Displacement 0.000365 0.001200 YES
Frequency file: MC_NH3BH3_FREQ.LOG
Low frequencies --- -0.1483 -0.0602 -0.0067 14.4291 16.6814 16.6904 Low frequencies --- 263.2246 631.4943 638.9660
optimised NH3BH3 molecule |
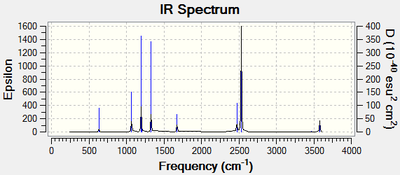
Vibrational spectrum for NH3BH3
| Wavenumber (cm-1) | Intensity (arbitrary units) | Symmetry | IR active? | Type |
| 263 | 0 | E | no | bend |
| 631 | 14 | E | very slight | symmetric stretch |
| 638 | 3 | E | very slight | bend |
| 638 | 3 | E | very slight | bend |
| 1086 | 40 | E | yes | bend |
| 1086 | 40 | E | yes | bend |
| 1196 | 109 | E | yes | bend |
| 1203 | 3 | E | no | bend |
| 1203 | 3 | E | no | bend |
| 1329 | 113 | E | yes | bend |
| 1676 | 27 | E | yes | bend |
| 1676 | 27 | E | yes | bend |
| 2472 | 67 | E | yes | symmetric stretch |
| 2532 | 231 | E | yes | asymmetric stretch |
| 2532 | 231 | E | yes | asymmetric stretch |
| 3463 | 2 | E | very slight | symmetric stretch |
| 3580 | 27 | E | yes | asymmetric stretch |
| 3580 | 27 | E | yes | asymmetric stretch |
|
Energy Calculation
E(BH3) = -26.61532
E(NH3) = -56.55776
E(NH3BH3) = -83.22469
ΔE = E(NH3BH3)-[E(NH3)+E(BH3)] = -0.05161 au = -135 KJ/mol
A carbon- carbon bond has an energy of formation of about -350 KJ/mol. Using this as a standard, the N-B bond is a weak bond at less than half the formation energy. This follows expectation as a C-C bond is quite strong and the expected bonding structure for NH3BH3 has the nitrogen lone pair attracted to the positively charge center of the unoccupied p-orbital of Boron without full orbital overlap, leading to an ionic type bond which would be weaker than the strong covalent C-C bond.
Smf115 (talk) 17:50, 23 May 2018 (BST)Correct calculation and consideration given to the accuracy of the reported results.
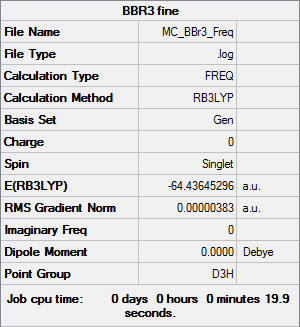
BBr3
B3LYP/6-31G(d,p),LanL2DZ
Item Value Threshold Converged? Maximum Force 0.000008 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000036 0.001800 YES RMS Displacement 0.000018 0.001200 YES
Frequency file: MC_BBr3_FREQ.LOG
Low frequencies --- -0.0137 -0.0064 -0.0046 2.4315 2.4315 4.8421 Low frequencies --- 155.9631 155.9651 267.7052
optimised BBr3 molecule |
Vibrational spectrum for NH3
| Wavenumber (cm-1) | Intensity (arbitrary units) | Symmetry | IR active? | Type |
| 155 | 0 | E | no | bend |
| 155 | 0 | E | no | bend |
| 267 | 0 | A1 | no | symmetric stretch |
| 377 | 3 | A1 | very slight | out-of-plane bend |
| 762 | 319 | E | yes | asymmetric stretch |
| 762 | 319 | E | yes | asymmetric stretch |
|
Aromaticity
Benzene
B3LYP/6-31G(d,p)
Item Value Threshold Converged? Maximum Force 0.000102 0.000450 YES RMS Force 0.000042 0.000300 YES Maximum Displacement 0.000165 0.001800 YES RMS Displacement 0.000081 0.001200 YES
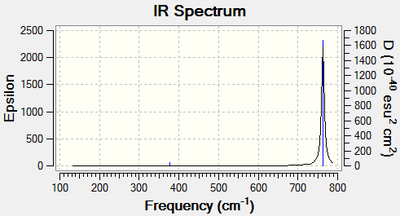
Frequency file: MC_Benzene_Freq.LOG
Low frequencies --- -0.0088 -0.0042 -0.0041 11.3041 11.3041 15.5388 Low frequencies --- 414.2825 414.2825 621.2723
Borazine
B3LYP/6-31G(d,p)
Item Value Threshold Converged? Maximum Force 0.000321 0.000450 YES RMS Force 0.000108 0.000300 YES Maximum Displacement 0.000678 0.001800 YES RMS Displacement 0.000270 0.001200 YES
Frequency file: MC_Borazine_Freq.LOG
Low frequencies --- -11.5654 -10.8953 -10.8953 -0.0239 -0.0239 -0.0187 Low frequencies --- 289.1233 289.1233 404.0960
Comparisons
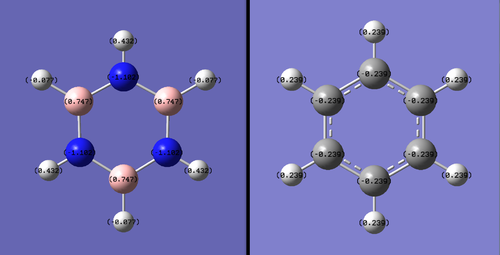
| Borazine vs Benzene Charge Distribution | Discussion |
|
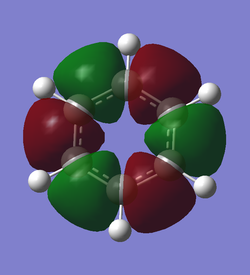
Benzene has a small charge separation between the carbons in the pi-system and the surrounding hydrogen, due to the higher stabilizing nature of the pi-system for electrons and the greater electro-negativity of carbon as opposed to hydrogen. The borazine, however is a much more complex system, with 4 separate charges present. The boron and nitrogen are positively and negatively charged respectively with the periphery hydrogen oppositely charged to its bonded atom. While the borazine molecule is symmetric and therefore does not have a dipole moment, its reactivity would be effected by its orientation in relation to the other reactant.
Another significant difference between the molecules is the extremity of charges between atoms within the same molecule. This is best represented in the lower figure; both molecules have their charges represented by the same color scale. Benzene's charges are much closer to zero than those present on borazine. All of these differences stem from the relative electro-negativity of the atom in each molecule. In benzene all the atoms in the pi-system are the same therefore have the same electro-negativity and share the charge equally. The ring atoms in borazine are boron and the more electro-negative nitrogen, this difference causes the disparity of charge between the two atoms. This is also responsible for the differences in the bonded hydrogen. |
Smf115 (talk) 17:47, 23 May 2018 (BST)Clearly illustrated charge distribution with the same colour range chosen across both molecule and cleare comparison. To improve, the explaination of the differences seen in the MOs due to the differences in the electronegativities could have been more detailed with the charges themselves referenced and other aspects, such as symmetry, mentioned.
| Borazine MO | Benzene MO | Discussion |
|
|
borazine MO 10 : benzene MO 12
This MO is particularly interesting because in benzene it is a wholly bonding orbital for every atom, but in the borazine molecule it lacks this bonding character between the boron and its bonded hydrogen. This is due to the lack of symmetry within the hydrogen as they are bonded to different elements. The effect of these hydrogen not participating in this overall bonding orbital would contribute to the longer B-H bond length compared to N-H, 1.19 Å and 1.00 Å respectively. While this MO may be non-bonding for some hydrogen it is also bonding between the ring atoms. The bonding sigma-pi orbitals have the additional feature of being bonding between the ring atoms in both structures and will have just a strong delocalization and stabilizing effect as the p-z aromatic structure. |
|
|
borazine MO 15 : benzene MO 14
This pair of MOs exemplifies that despite the large differences in elemental groups and amount of overall symmetry, the molecules share much in common. These molecular orbitals are simple pi-bonding orbitals of the planar pi atomic orbitals that do not interact with the sigma orbitals or the conjugated pi-system. The most important factor in the similarity is that they do not interact with the sigma orbitals. This is also discussed in the previous pair of MOs. Since the hydrogen are in different environments, determined by its bonded element, they participate in the molecular orbitals separately. In benzene this is not true and therefor these differing hydrogen orbital interactions is the main factor for the structural differences in the MOs of the two molecules. Since these pi-bonding orbitals do not interact with these hydrogen sigma orbitals at all, there is almost no structural difference between the two MOs. |
|
|
borazine MO 18 : benzene MO 19
This is again an example of a pair of very similarly structured bonding MOs. This pair is however less identical and this shows a new difference that can arise from the differing ring elements. In borazine it can be seen that orbitals that involve boron pi-orbitals are more diffuse than those of the nitrogen pi-orbitals (bottom boron pi-sigma bonding orbital and on the top ring bridging structure). Borons valence orbitals are larger than those of nitrogen since nitrogen has a higher effective nuclear charge that creates a contraction of its atomic radii. This difference in orbital radii can directly be seen in the MO. The benzene MO is perfectly symmetrical in its orbital diffuseness because the ring molecules all have the same orbital size. |
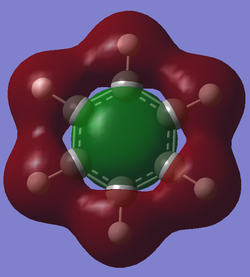
The calculated molecular orbital can be interpreted to the same end as the simple aromatic assumptions. These molecular orbitals show that there is a stronger bond than a single bond as the z orbital overlap in an additional pi-bonding orbital and creates a disk shaped structure that interconnects all ring atoms. This also shows that since a completed ring is needed to have this effect, if a new bond would use a z-p orbital, the aromaticity would be broken. It also shows that large electron density is present above and below the plane of the ring.
The generated MOs go a bit further than the standard overlapping p-z AO overlap theory, in creating a realistic structure and from this some differences can be found. In the AO theory a ring shaped structure is formed from the atomic orbitals, but with the generated orbital a ring is not what is seen. A full disk shape is seen and this can have profound effect on the overall energy of the bonds made as every pi orbital is overlapping to every other atom rather than just its neighboring ring atoms. This can be taken a step further by stating that if it is not the ring nature of the overlap that makes it aromatic, then the planar nature of the overlap may not be necessary either. The presence of MO pi-overlap that is shared between many atoms in a singular molecule may be the only differentiating factor between aromatic and non-aromatic structures.
In addition to this the most interesting structure in the lab was the first pair of orbitals mentioned above. The delocalized structure of the internal half of sigma-pi orbitals would contribute just as highly to the aromatic stability as the p-z overlap. Also, even when the hydrogen was not active in the sigma-pi orbital ,the internal delocalization was conserved. Extrapolating from this, the substituted group might have no effect on this internal delocalization and it would then be a consistent structure among all aromatic structures. In the paper linked in the instructional wiki page (10.1002/chem.200700250) it stated in the introduction that the p-z overlap was easily broken or weakened by conformation changes and yet "aromaticity" was uncahanged. In these conformation changes, however, the sigma-pi delocalization would be conserved. This made me redefine aromaticity personally from p-z conjugation to all kinds of delocalization, perhaps even especially this sigma-pi form.
Smf115 (talk) 17:47, 23 May 2018 (BST)Some good ideas are raised and the discussion of aromaticity and the MO comparison has cleary been thought through. However, the correct terminology isn't always used and I think there is confusion between p- and s- AO contributions and describing interactions within an MO as sigma- or pi-type. For example, MO 14 and 15 arise from p-orbital contributions which have strong sigma-interactions between the adjacent in-phase lobes. It would have been nice to see the key concepts of aromaticity discussed more and the same confusion between some terms meant some of the ideas raised aren't correct.
Smf115 (talk) 17:47, 23 May 2018 (BST)Overall a good attempt with mistakes made across both sections.