Cid:01560585
Overall this is a good report with all parts answered. There are instances where a more in depth answer could have been given. See comments below, but remember to think if the answers you have calculated do make sense from the knowledge you already have. Mys18 (talk) 14:02, 1 June 2020 (BST)
On a potential energy surface diagram, how is the transition state mathematically defined? How can the transition state be identified, and how can it be distinguished from a local minimum of the potential energy surface?
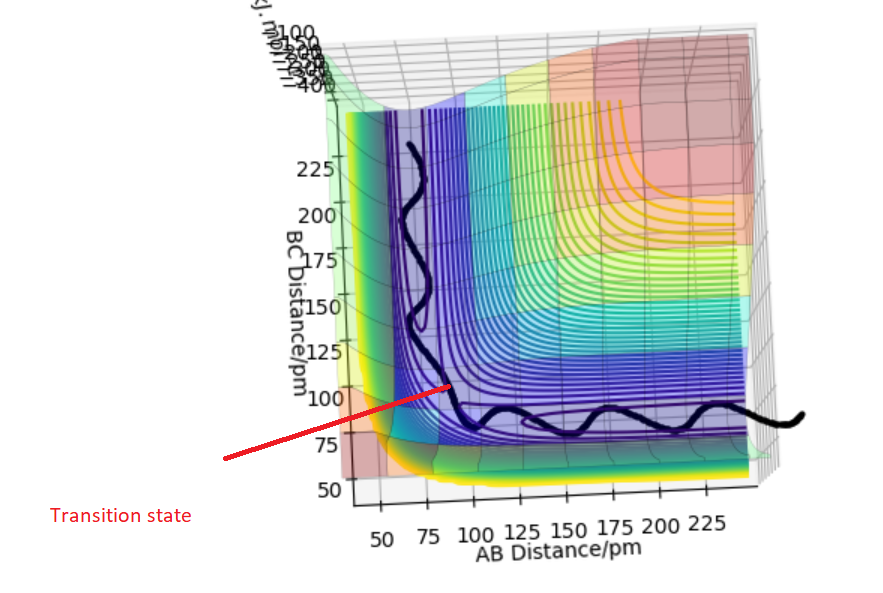
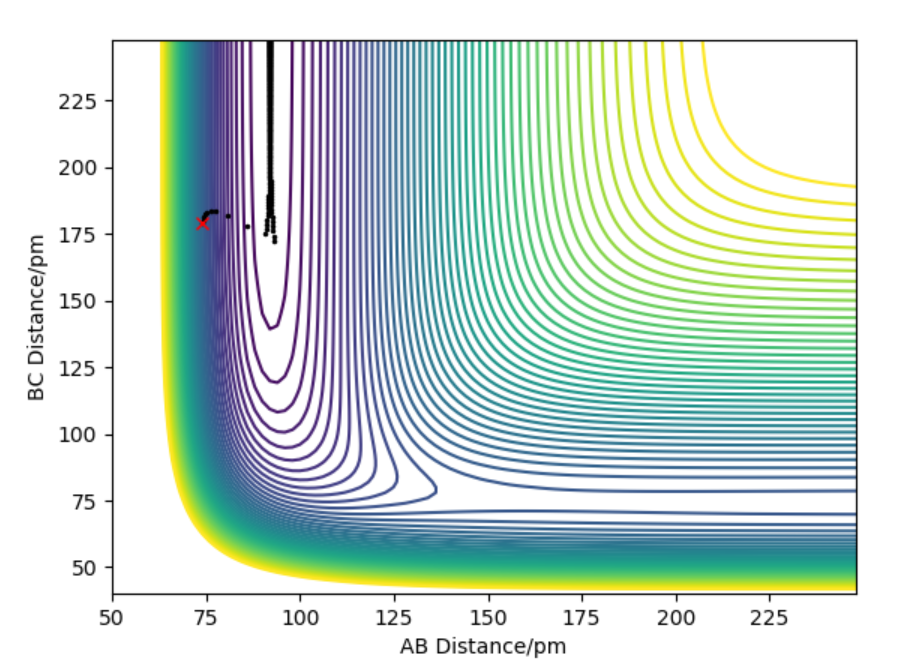
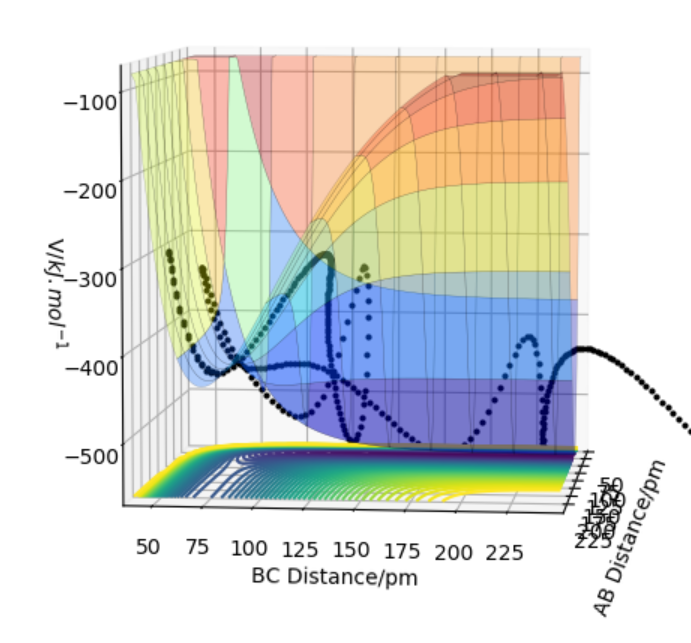
The transition state is a maximum on minimum energy path that links reactants and the products. It is a point where first derivative ∂V(ri)/∂ri=0 which means the gradient of the potential is zero.It's found by locating saddle point. A saddle point is position on the potential energy surface(Figure 1) that corresponds to a minimum in all directions except one.This means there is a negative curvature in one direction and positive curvature in all other and the curvature is found by second derivative.
Good the gradient is zero in all orthogonal directions making the TS neither a minimum or a maximum. I think the differentiation between the TS and a local minimum could be slightly more clear, remember always discuss the counter point, so in this case you are missing details on a local minimum. So the second derivative for a local minimum will always be >0 whilst for a TS the saddle point second derivative will be what you have described - negative to one axis and positive to the other which then means the TS is a local minima in one direction and a local maxima in the other orthogonal direction.Mys18 (talk) 12:27, 1 June 2020 (BST)
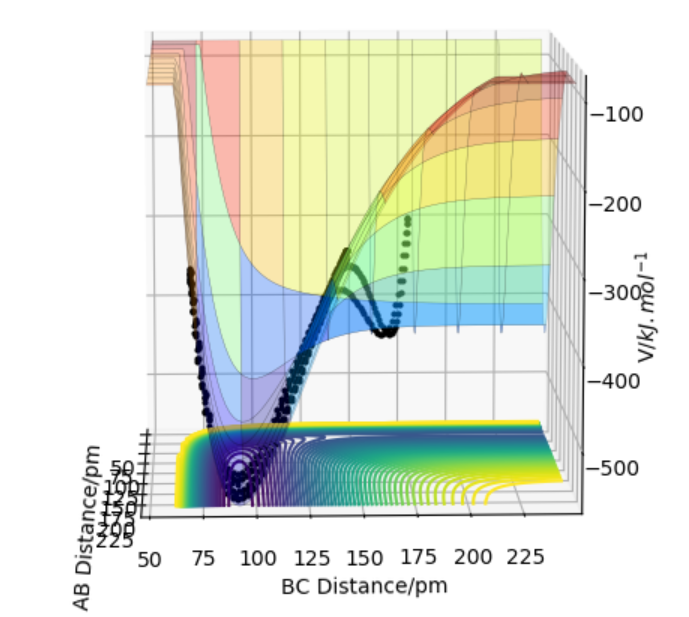
Figure 1) Potential Energy Surface for H+H2 system.The black line represents the minimum energy path.
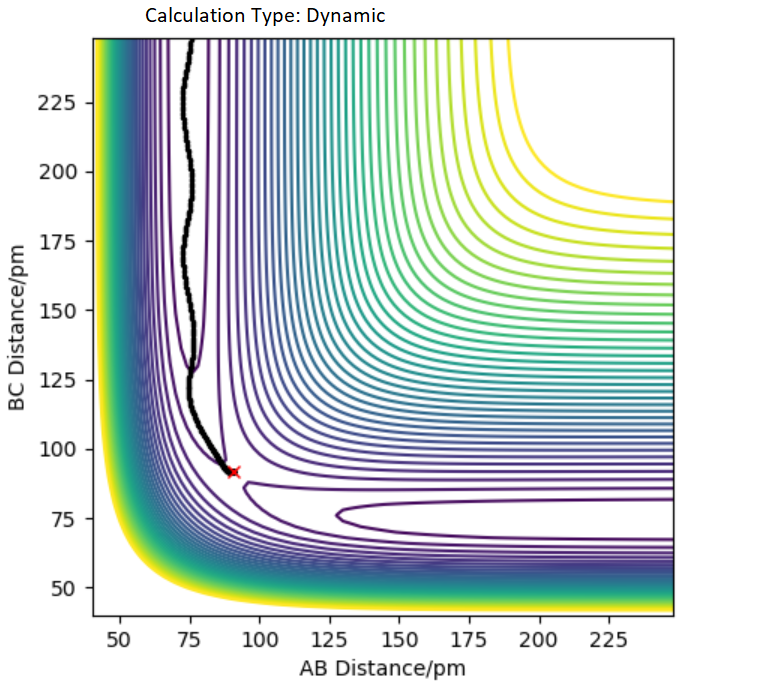
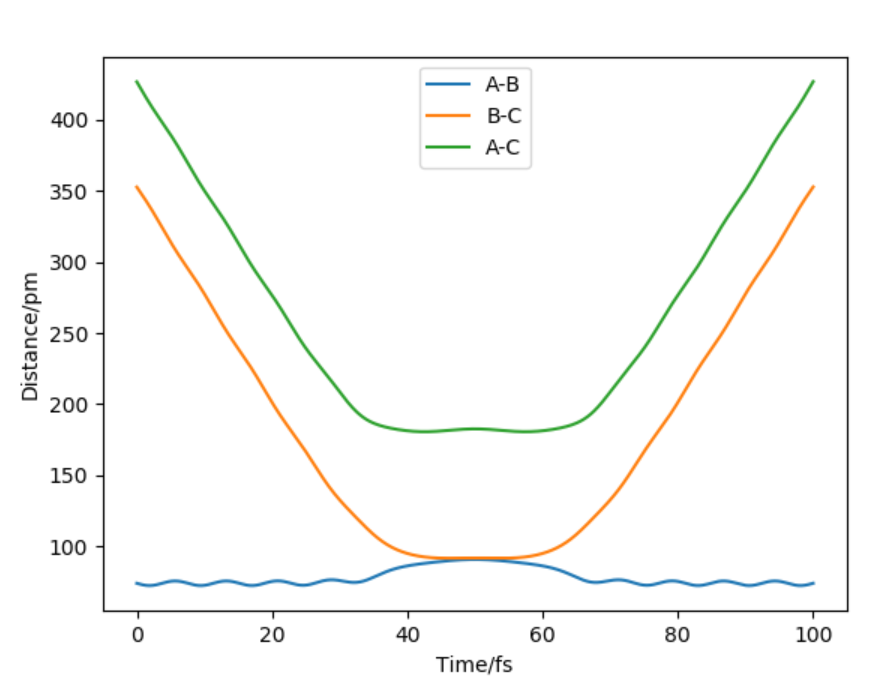
Report your best estimate of the transition state position (ts) and explain your reasoning illustrating it with a “Inter nuclear Distances vs Time” plot for a relevant trajectory.
I would have imagined a value closer to zero for AB BC 90 pm...but otherwise good estimates and discussion. Think about why your figure has non linear slopes and what this means wrt. r1 and r2.Mys18 (talk) 14:05, 1 June 2020 (BST)
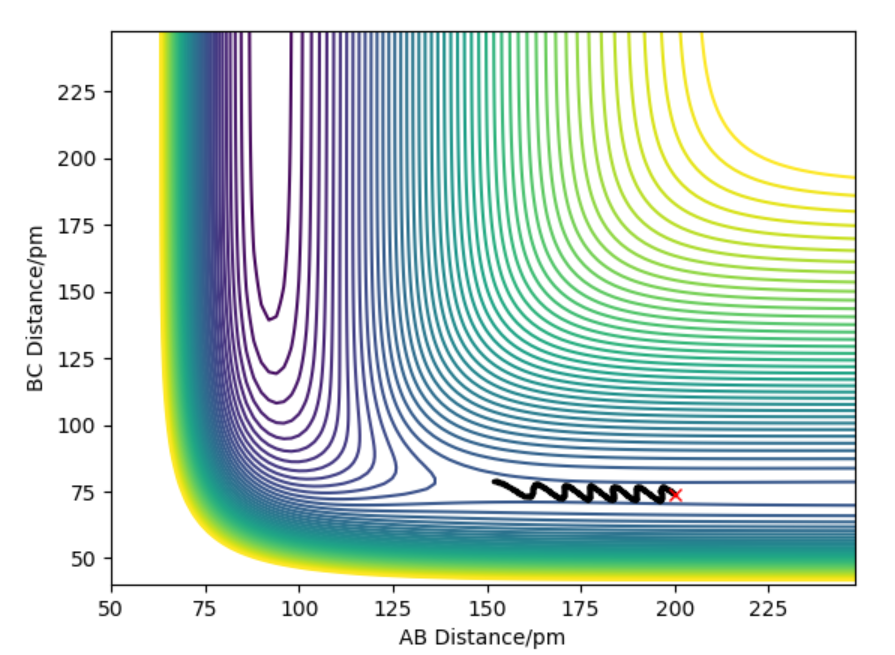
Hammond's postulate states that transition states(ts) resembles reactant or product depending on whether reaction is exothermic or endothermic. In this case transition state is symmetrical therefore AB=BC at ts.In transition state force = 0 . When distance of AB=BC=90 pm it gives a force of +0.132 kj/mol-1pm-1(repulsive) along both bonds but when the the distance is AB=BC=92 it gives force of -0.197 kj/mol-1pm-1(attractive) along both bonds.Force will equal zero in between these two bond lengths and ts could be found by through using inter nuclear distance vs time graph(Figure 2).
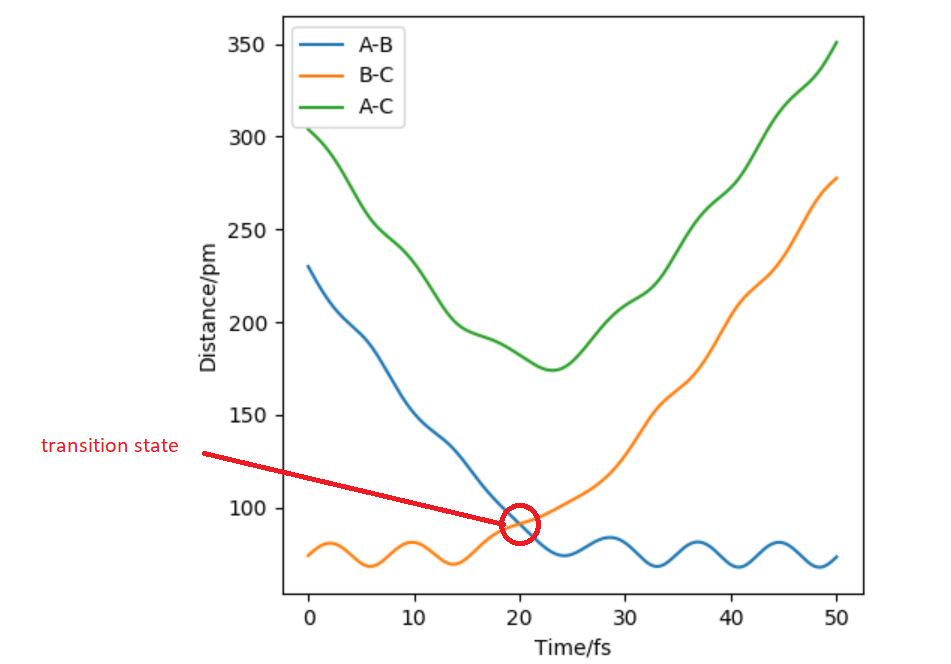
Figure 2: Hammond's postulate states that transition states resembles reactant or product depending on whether reaction is exothermic or endothermic. In this case ts is symmetrical therefore AB=BC at TS BC=AC at r=90.8 pm
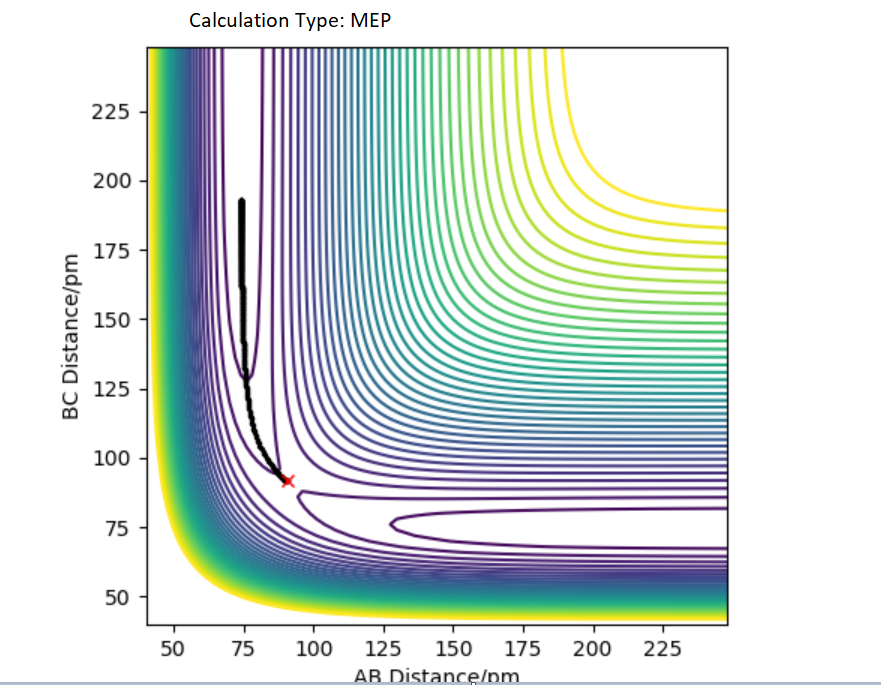
Comment on how the MEP and the trajectory you just calculated differ.
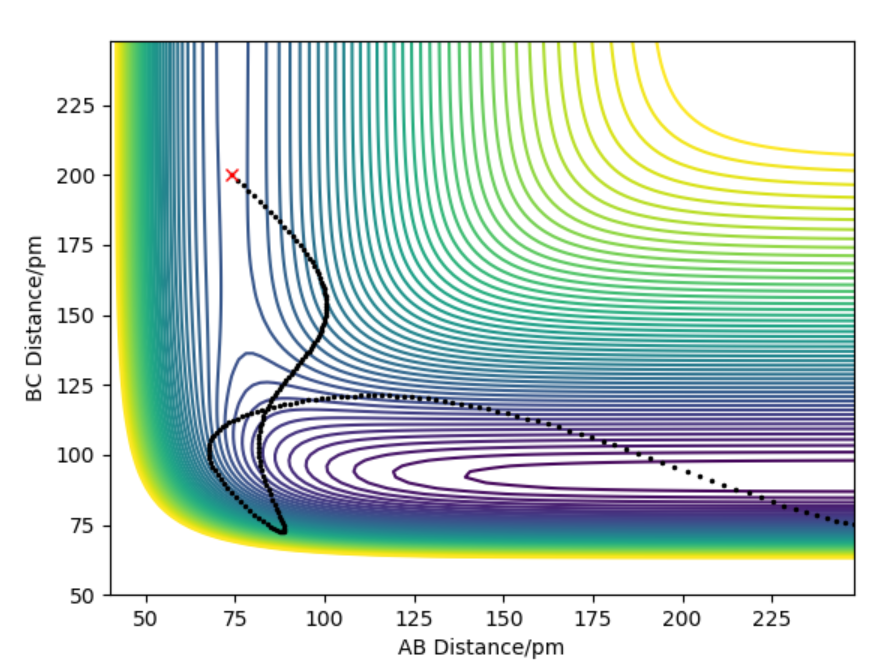
Compare to dynamic, MEP doesn't account of vibrations that result from the motions of atoms during a reaction.
Good, you have included figures, so another piece of advice, always refer to them in your written answer, in your case you could discuss how the line is more 'wavy' in the Dynamic trajectory but more 'smooth' in the MEP trajectory because there's no vibrational energies therefor not oscillating MEP. This compliments and supports your statement too! What about the differences in the total energy (KE and potential energy) of the system in the MEP and Dynamic? Mys18 (talk) 12:41, 1 June 2020 (BST)
Setup a calculation where the initial positions correspond to the final positions of the trajectory you calculated above, the same final momenta values but with their signs reversed.
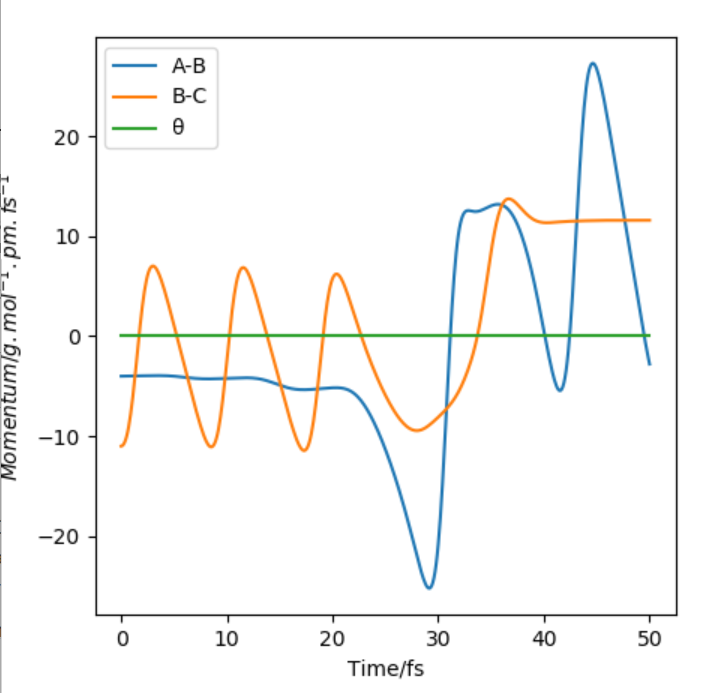
Momentumvstime:
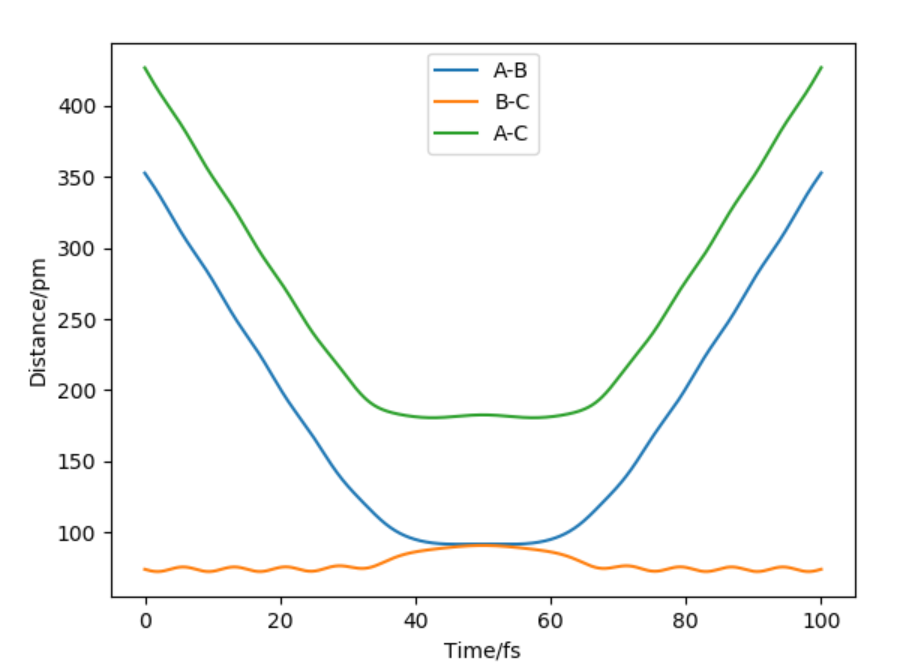
For AB=91.8 pm and BC=90.8 pm , AB plateaus 5.07 g mol -1.pm.fs-1 and BC oscillates at 3.21 g mol -1.pm.fs-1
For AB=90.8 pm and BC=91.8 pm, BC plateaus at 5.07 and AB oscillates at 3.21 (g mol -1.pm.fs-1)
Distancevstime:
For AB=91.8 pm and BC=90.8 pm, BC oscillates at 74.02 pm where as AB increases to 352.63 pm(50 fs)
For AB=90.8 pm BC=91.8 pm, AB oscillates at 74.02 pm where as BC increases to 352.63 pm
Setup a calculation where the initial positions correspond to the final positions of the trajectory you calculated above, the same final momenta values but with their signs reversed.
What do you observe?
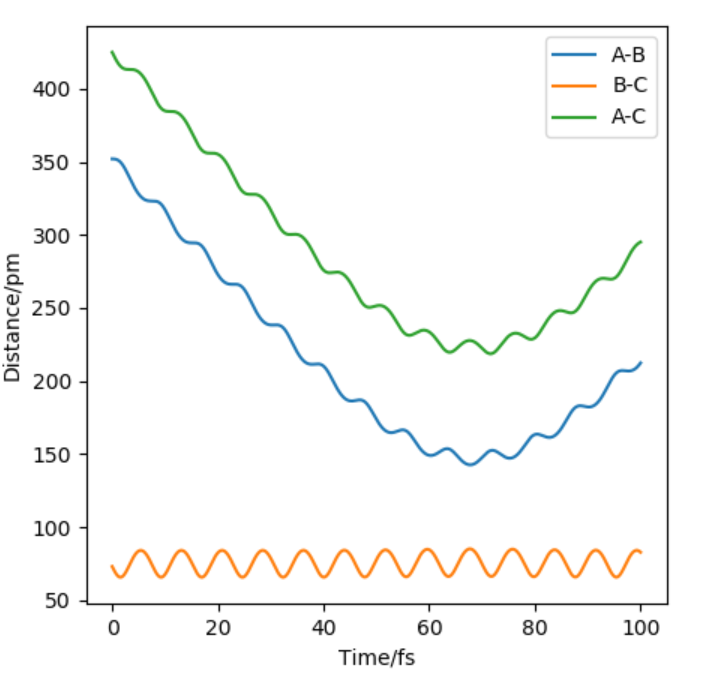
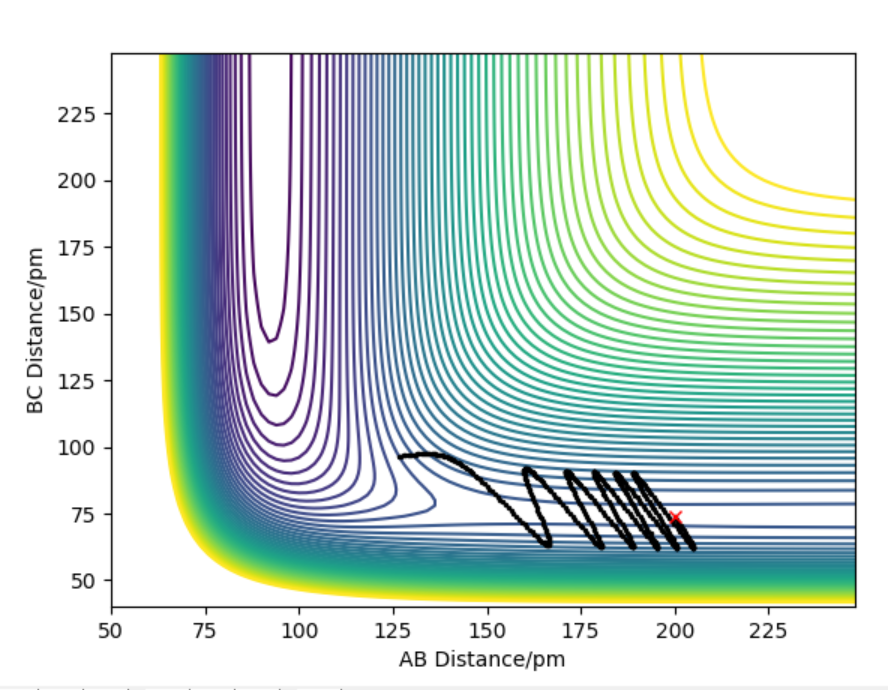
First scenario where AB=74.02 and BC=352.63 and momentum=-5.07 and -3.21 respectively shows that initially BC come together to AC but move away from each other as momentum and energy is not enough to bring them together to transition state and overcome the energy barrier to go to reactants. (BC +A)
For other scenario, same thing happens but in reverse such that energy is not enough to overcome the transition state barrier and so it cant form the products (AB + C).
Inter nuclear vs Time graph for initial condition where AB= 352 and BC=73 momentum=-2.5 and -5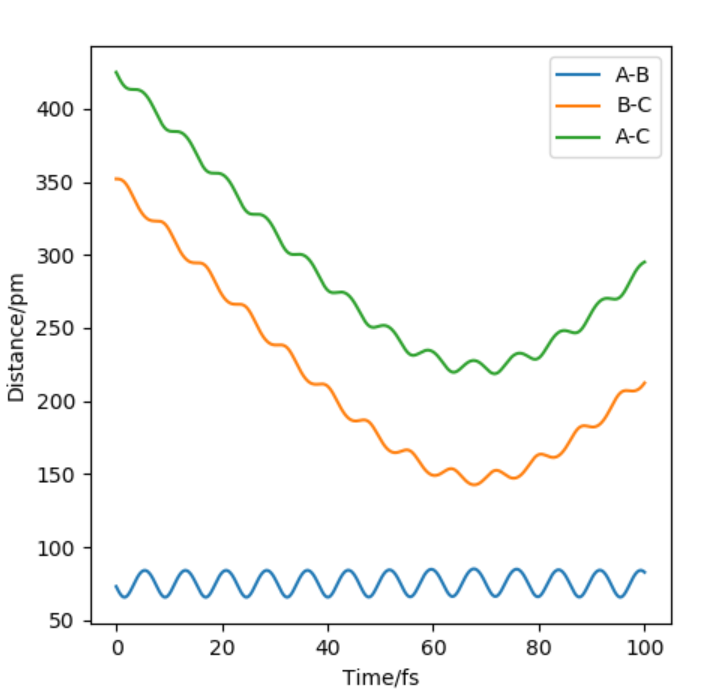
Inter nuclear vs Time graph for initial condition AB= 73 and BC=352 momentum=-5 and -2.5
For the initial positions r1 = 74 pm and r2 = 200 pm
| p1/ g.mol-1.pm.fs-1 | p2/ g.mol-1.pm.fs-1 | Etot | Reactive? | Description of the dynamics | Illustration of the trajectory |
|---|---|---|---|---|---|
| -2.56 | -5.1 | -414.28 | Yes | Enough energy is supplied to overcome the transition state( breakage B-C bond and formation A-B bond). The product is formed and the excess energy is transferred to vibration energy shown by oscillatory energy path. | 
|
| -3.1 | -4.1 | -420.077 | No | Energy is not enough to over come the energy barrier so transition state is not reached. B-C is not broken and A-B can't be formed. | 
|
| -3.1 | -5.1 | -413.977 | Yes | Enough energy is supplied to overcome the transition state( breakage B-C bond and formation A-B bond). The product is formed and the excess energy is transferred to vibration energy shown by oscillatory energy path. | 
|
| -5.1 | -10.1 | -357.277 | No | Enough is supplied to overcome the transition state (shown by formation of A-B bond and breakage of B-C bond) but the system reverts back to form reactants. This is called barrier recrossing. This happens because the product that forms have a high energy that it can break the bond and reverses the reaction to form reactants back again. | 
|
| -5.1 | -10.6 | -349.477 | Yes | More than enough energy is supplied to overcome the transition state( breakage B-C bond and formation A-B bond) and the excess energy is transferred as vibration energy which is shown by oscillatory energy path. | 
|
Great job!Mys18 (talk) 12:55, 1 June 2020 (BST)
Given the results you have obtained, how will Transition State Theory predictions for reaction rate values compare with experimental values?
The transition state theory predicts that the rate constant for a generic bi-molecular reaction is proportional to temperature and for the reaction the kinetic energy along the the reaction coordinate follows the Boltzmann distribution. If the temperature is increased the speed of reactant molecules would increase so therefore they would possess higher kinetic energy. This would increase the collision rate and as the theory predicts, the trajectory would be reactive since the trajectory has a higher kinetic energy along the reaction coordinate than the activation energy. However, it fails to consider cases such as barrier recrossing where the reactants posses high enough kinetic energy for trajectory to reach activation energy but it forms products with high energy(vibration energy) that could break the bond and reverses the reaction to form the reactants. Therefore, in this case transition state theory has overestimated the rate as it assumes all reactions go to completion if they have enough kinetic energy. Transition state theory treats energy classically so ignores the tunneling effect which underestimates the transition state. However, since tunneling has a smaller effect compared to barrier recrossing, transition states theory is mainly an overestimate of rate.
Perfect!Mys18 (talk) 12:55, 1 June 2020 (BST)
By inspecting the potential energy surfaces, classify the F + H2 and H + HF reactions according to their energetic (endothermic or exothermic). How does this relate to the bond strength of the chemical species involved?
Locate the approximate position of the transition state.Report the activation energy for both reactions.
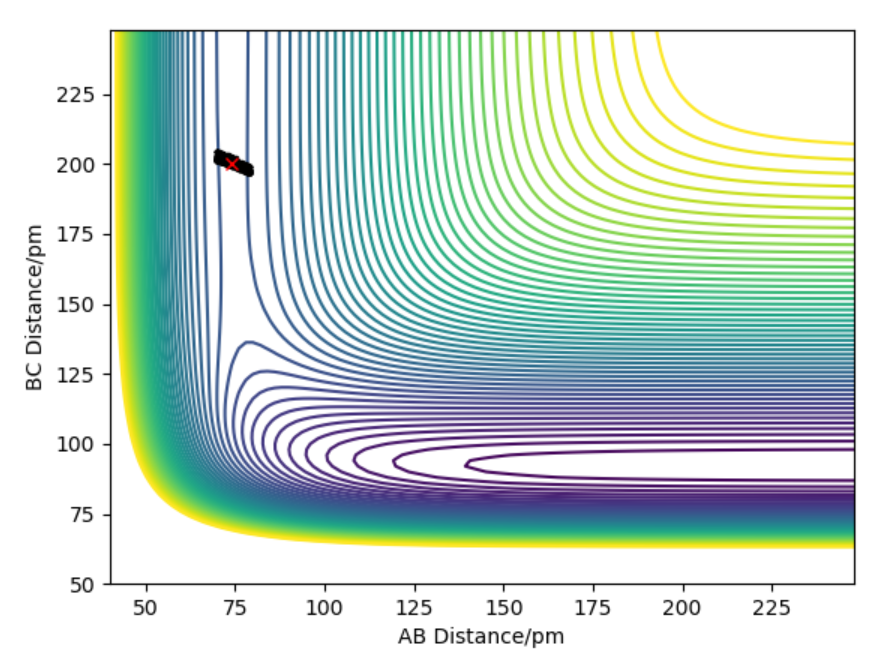
F + H2 PES: The plot shows that this reaction is exothermic which can be seen by reactants being higher in energy than the products . This suggest that H-H bond(74 pm) is stronger than the F-F(94 pm) bond that is formed so therefore more energy is needed to break H-H bonds. This is why the reactants are higher in energy compared to products as shown in the contour plot of F+H-H below.
Good. What bonds are we comparing, should it not be H-H and H-F? I would imagine H-F bond strength is > H-H using my chemistry intuition/literature bond energy values...with the stronger H-F bond we would see release greater energy giving the exothermic reaction... Mys18 (talk) 13:03, 1 June 2020 (BST)
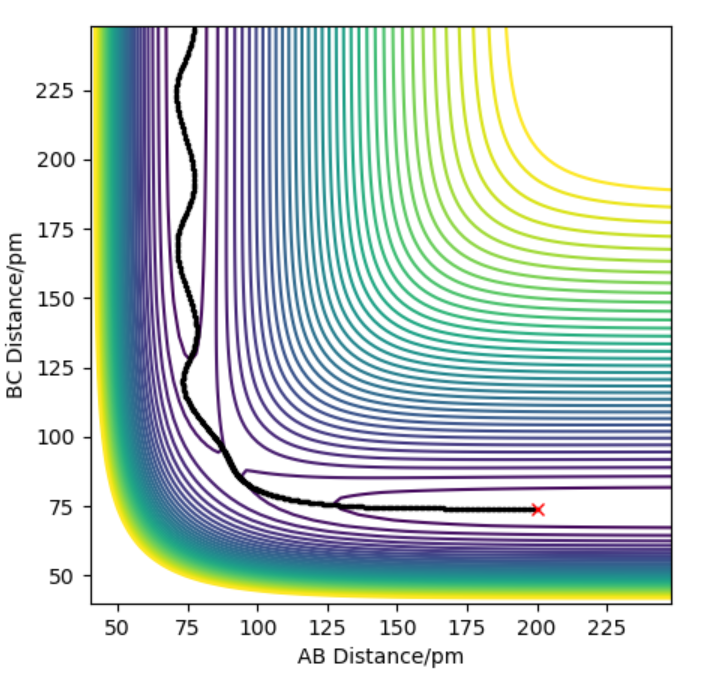
To locate the transition states of this reaction, the bond lengths were adjusted such that gave force along both bonds(H-F and H-H) to be equal to zero.To do this Hammond postulate was used which states that the transition state of a reaction resembles either the reactants or the products, to whichever it is closer in energy. This reaction is an exothermic so the reactant resembles the transition state of the reaction. This means that in transition state the bond length of H-H would be similar to what its like in reactant. The bond length of H-H is 74 so if we keep that same in transition state and change the bond length of H-F(181.4 pm) until force equal zero along both bonds, we will be able to locate the transition state for F + H-H reaction.
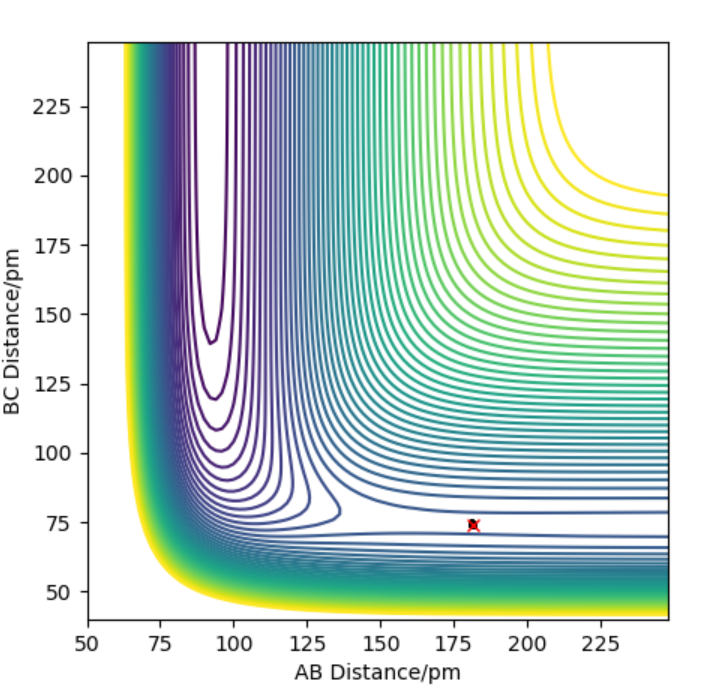
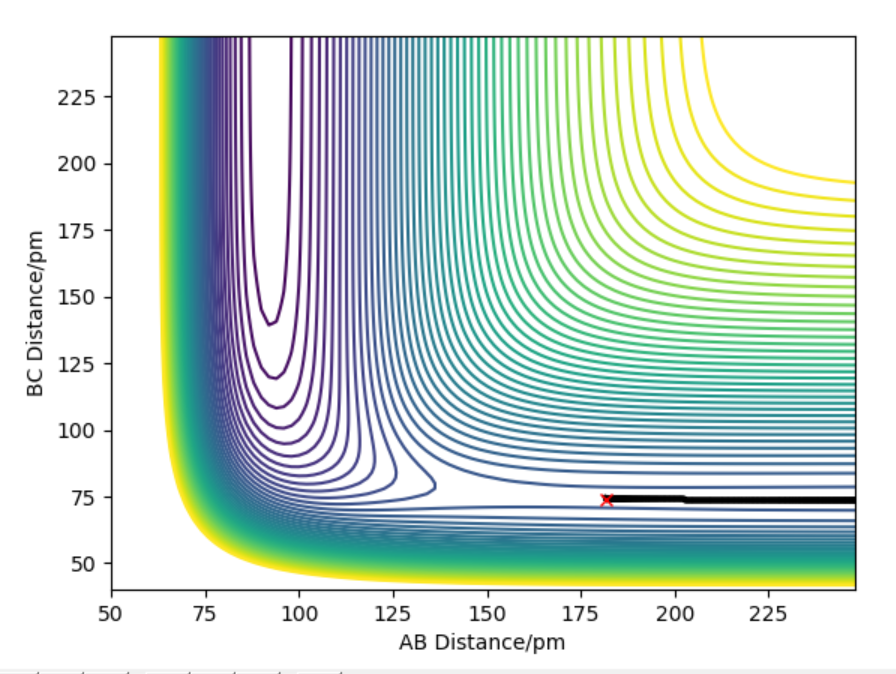
The contour plot indicating transition point which is marked (X). AB = 181.4 pm and BC= 74 pm
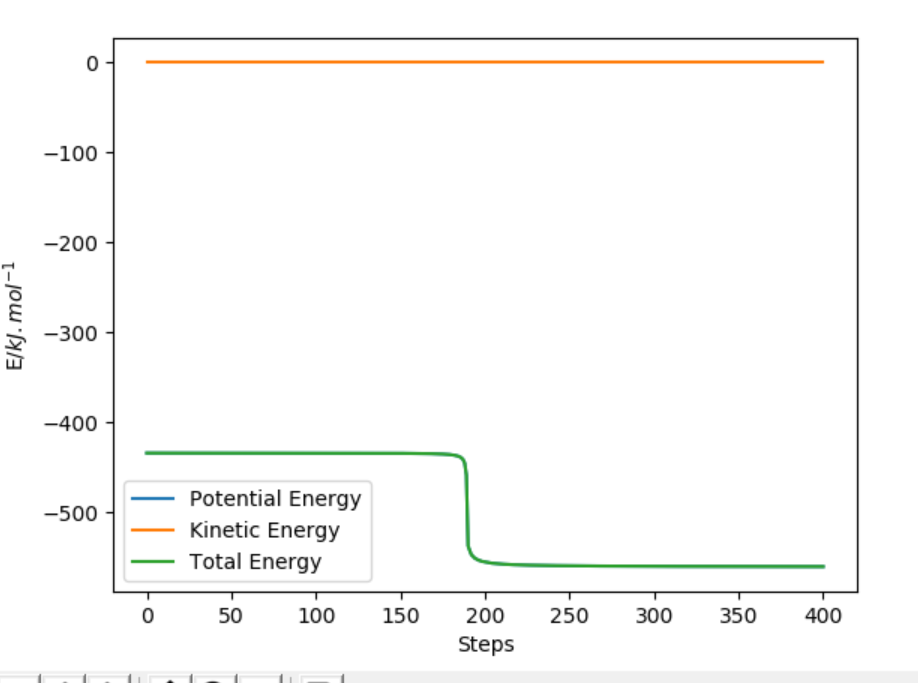
The activation energy is found by finding the energy difference of reactants and the transition state. Since, the energy of transition state is -433.942 kJ.mol-1 which is found at points when forces equal zero(AB=181.4 and BC=74). If we move away from the transition state towards the reactants by increasing the AB distance(181.9 pm) and keeping BC distance the same, we can get the energy of reactants by using MEP calculations which gives the closest energy minima. This would correspond to the reactants energy. The energy of the reactant was found to be -435.100 kJ.mol-1 therefore the activation energy is 1.056 kJ.mol-1. This is shown in energy vs time plot and contour plot which shows that the energy path goes back to the reactant.
Counter plot of F+H-H (AB=181.9 and BC=74)
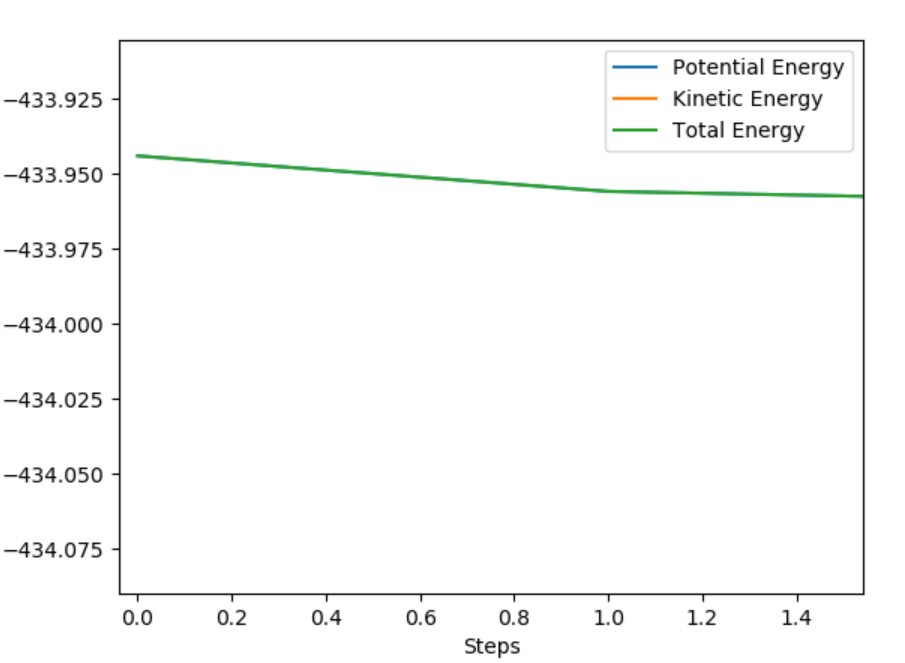
Energy vs Time Showing activation energy of F+H-H reaction
H + HF PES: The plot shows that this reaction endothermic which can be seen as products are in higher energy than the reactants . This suggest that H-F bond(92 pm) is weaker than the H-H(74 pm) bond that is formed so therefore less energy is needed to break H-F bonds. This is why the products are lower in energy compared to the reactants as shown in the contour plot of H +H-F below.
Does it make sense the H-F bond is weaker than H-H, think about your bonding knowledge? Mys18 (talk) 13:51, 1 June 2020 (BST)
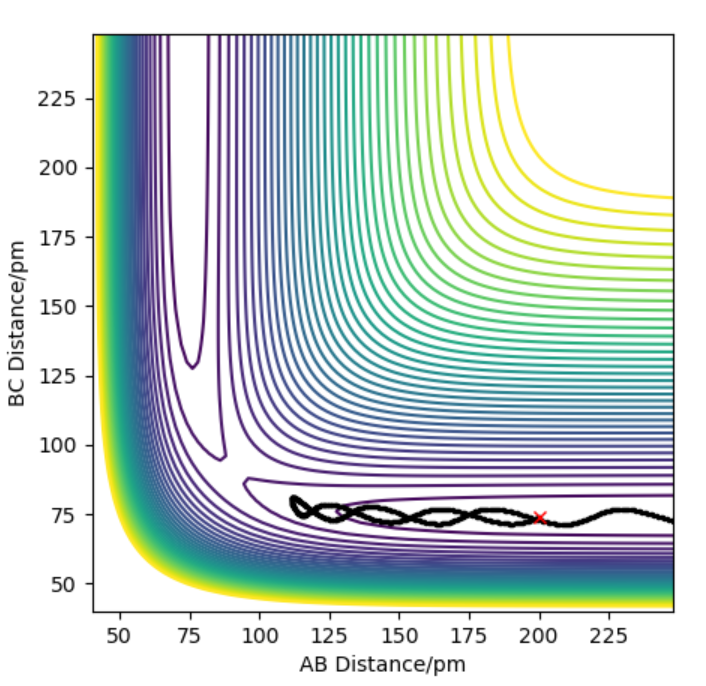
To locate the transition states of this reaction, the bond lengths were adjusted such that gave force along both bonds(H-F and H-H) to be equal to zero.To do this Hammond postulate was used which states that the transition state of a reaction resembles either the reactants or the products, to whichever it is closer in energy. This reaction is an endothermic so the product resembles the transition state of the reaction. This means that in transition state the bond length of H-H would be similar to what its like in product. The bond length of H-H is 74 so if we keep that same in transition state and change the bond length of H-F(181.4 pm) until force equal zero along both bonds, we will be able to locate the transition state for H + HF reaction.
Good inclusion of your methodology.Mys18 (talk) 13:51, 1 June 2020 (BST)
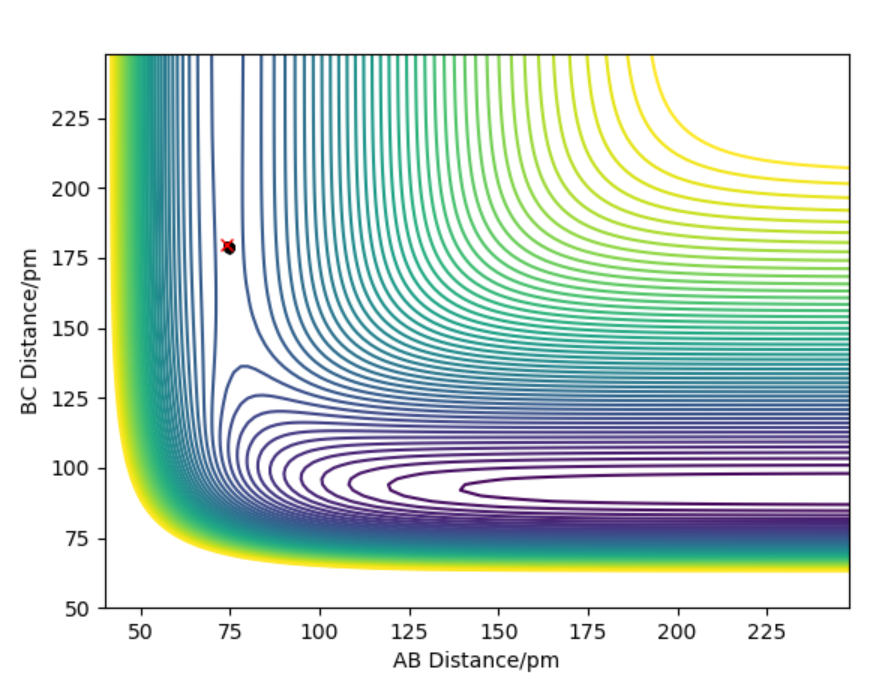
The contour plot indicating transition point which is marked (X). AB = 74 pm and BC= 181.4 pm
The activation energy is found by finding the energy difference of reactants and the transition state. Since, the energy of transition state is -433.937 kJ.mol-1 which is found at points when forces equal zero(BC=181.4 pm and AB= 74 pm). If we move away from the transition state towards the reactants by decreasing BC (179) and keeping AB distance(74) the same, we can get the energy of reactants by using MEP calculations which gives the closest energy minima. This would correspond the reactants energy. The energy of reactant was found to be -557.100 kJ.mol-1 therefore the activation energy is 124 kJ.mol-1. This is shown in energy vs time plot and contour plot which shows that the energy path goes back to the reactant.
These are good approximations and units :).Mys18 (talk) 13:51, 1 June 2020 (BST)
Counter plot of H+H-F (AB=74 and BC=179)
Energy vs Time Showing activation energy of H+H-F reaction
The answers to questions in this section were somewhat scattered, may be worth going back to check that your report is logically laid out so no marks are missed in your answers :). Mys18 (talk) 14:01, 1 June 2020 (BST)
In light of the fact that energy is conserved, discuss the mechanism of release of the reaction energy. Explain how this could be confirmed experimentally.
The reactive trajectory chosen has AB=225 pm, BC= 74 pm and the momentum was -4 and -11 respectively. To describe the mechanism of the reaction (F+H-H) momentum/time plot shown below was used.To confirm this experimentally, chemiluminescence(monitor reaction by monitoring colour) and IR could be used. At the start of the reaction, Bond A-B(F-H) is moving with transnational energy and B-C(H-H) is oscillating with vibration energy. H-H bond which is oscillating with vibration energy will not be detected in IR because it doesn't have a change in dipole which is one of the selection rule. After the collision, A-B bond (H-F) has vibration energy and shows oscillatory behavior but B-C bond(H-H) moves away with transnational energy with little or no vibration energy.
Nice. Chemiluminescence to moinore the emission of infrared radiation. The reaction also generates heat...another potential technique to use?Mys18 (talk) 14:01, 1 June 2020 (BST)
Momentum/Time plot of reactive trajectory(AB=225 pm, BC= 74 pm and the momentum was -4 and -11 respectively)
Setup a calculation starting on the side of the reactants of F + H2, at the bottom of the well rHH = 74 pm, with a momentum pFH = -1.0 g.mol-1.pm.fs-1, and explore several values of pHH in the range -6.1 to 6.1 g.mol-1.pm.fs-1 (explore values also close to these limits). What do you observe? Note that we are putting a significant amount of energy (much more than the activation energy) into the system on the H - H vibration.
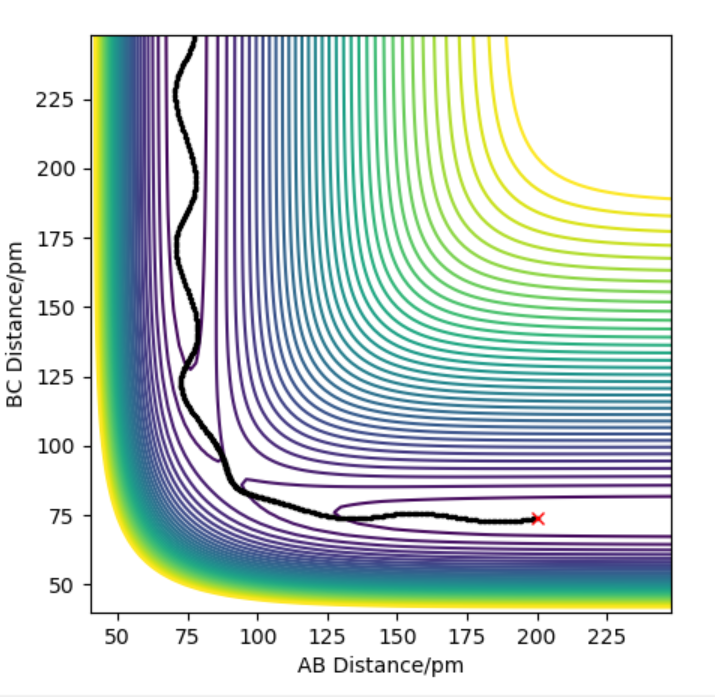
The reaction F+F-H has an early transition state so if high energy is put into the system, the reaction doesn't happen and in PES it doesn't go all the way to the products.This is shown in contour plot shown below for the system where H-H=74 pm, F-H= 200 pm and their momentum is set to -6.1 g.mol-1.pmfs-1 and -1 -6.1 g.mol-1.pmfs-1 respectively.
contour plot for the system where H-H=74 pm, F-H= 200 pm and their momentum is set to -6.1 -6.1 g.mol-1.pmfs-1 and -1 -6.1 g.mol-1.pmfs-1 respectively
For the same initial position, increase slightly the momentum pFH = -1.6 g.mol-1.pm.fs-1, and considerably reduce the overall energy of the system by reducing the momentum pHH = 0.2 g.mol-1.pm.fs-1. What do you observe now?
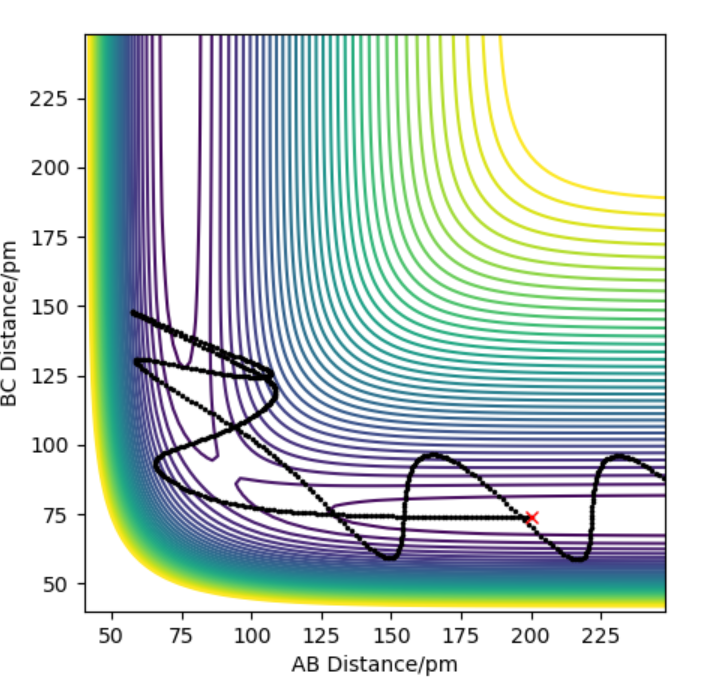
Even if the energy is reduced, the reaction doesn't proceed to form the products. This concept is explained by considering Hammond postulate and Polanyi's rule which shows that if the reagent has a vibration energy and the reaction has an early transition state, it will not form products.
Contour plot for F+H-F reaction where H-H =74 pm, F-H= 200 pm and their momentum is set to 0.2 -6.1 g.mol-1.pmfs-1 and .1.6 -6.1 g.mol-1.pmfs-1 respectively
Setup initial conditions starting at the bottom of the entry channel, with very low vibrational motion on on the H - F bond, and an arbitrarily high value of pHH above the activation energy (an H atom colliding with a high kinetic energy).
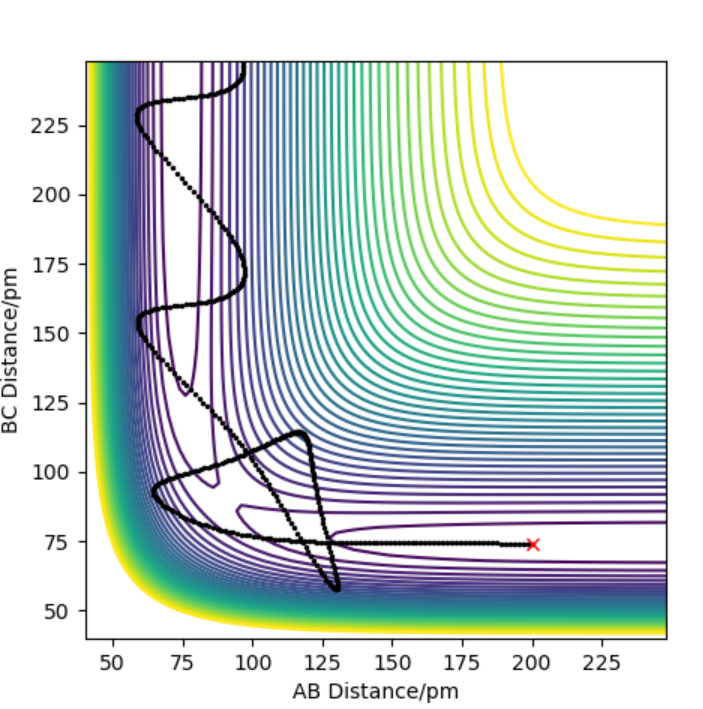
Polanyi's rule states that if vibration energy of reactant is not high for late transition reactions, the reaction will not proceed. This is shown on the contour plot below where the vibration energy supplied to reactant was high therefore the reaction does proceed.
Try to obtain a reactive trajectory by decreasing the momentum of the incoming H atom and increasing the energy of the H - F vibration. Polanyi's rule states that if vibration energy of reactant is not high for late transition reactions, the reaction will not proceed. This is shown on the contour plot shown below where vibration energy supplied to reactant was not high therefore the reaction does not proceed.
Discuss how the distribution of energy between different modes (translation and vibration) affect the efficiency of the reaction, and how this is influenced by the position of the transition state.
Hammond's postulate and Polanyi's Rule sum ups up how the different modes affect the efficiency of the reaction. 4 contour plots above shows how changing vibration energy affect whether the reaction proceeds or not. Generally, if the reaction has an early transition state, then the reaction will be proceed if the reactant has high translation energy but for a reaction with late transition sate,the reaction will only proceed efficiently if the reactant has high vibration energy.
Good understanding of Polyanis rule.Mys18 (talk) 14:01, 1 June 2020 (BST)