Cg1417MRDLab

Exercise 1

Question 1

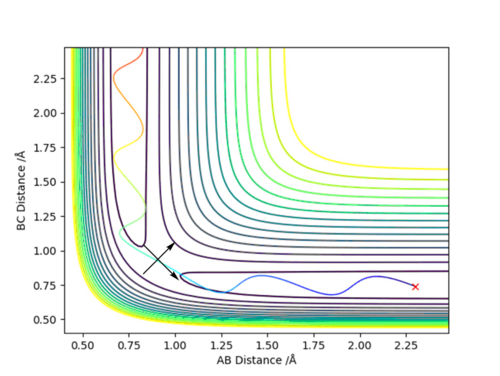
A transition state is mathematically defined as a saddle point where both f_x and f_y = 0 and f_xxf_yy < f_xy², where x and y are axes vectors. In this case, x and y must be redefined as such that the x runs tangential to the maximum along the lowest energy pathway as such that f_x = 0 and f_xx < 0, and y runs perpendicular to this axis as such that f_y = 0 and f_yy > 0.

How did you arrive there, and how do you define f_something? In chemistry, usually the df/dx notation is used to give derivatives. Also, I would include references here. I can't blame you for not giving references as it is very basic maths, but better safe than sorry. Fdp18 (talk) 20:46, 11 May 2019 (BST)

.

The two lines represent the new axis that have to be defined to find the transition state of this reaction. The transition state corresponds to the this maximum along the minimum energy reaction pathway or saddle point.

A local minimum is defined as having both f_x and f_y = 0 where f_xx > 0 and f_xxf_yy > f_xy², which is differs from the criteria provided for a saddle point mentioned previously.

The redefinition of the coordinate system with these vectors is helpful for understanding, but not mathematically necessary. Fdp18 (talk) 20:52, 11 May 2019 (BST)

To further on Frederik's comment: if you are using the condition involving the crossed partial derivative ∂_xxV × ∂_yyV < (∂_xyV)², then your x and y coordinates can be your r_AB and r_BC coordinates. The merit of the rotated system of coordinates you describe, is that the cross derivative ∂_xyV in that case is zero, and one can reason only about curvature along x and curvature along y. In this rotated system, at the transition state, one can identify the reaction coordinate as the direction where curvature is negative. João (talk)

Question 2

The position of the transition state from the contour plot can be approximated as around 0.9 Angstrom. A plot of internuclear separation against time plot will show any variation in the separation between A and B and then B and C. No variation will indicate a good approximation for the position of the transition state.

Figure 1 - Contour plot showing the region in which the TS lies

Figure 2 - Internuclear Separation against time graph with AB separation = BC separation = 0.90 Angstrom, with some oscillation in the separation

Figure 3 - Internuclear Separation against time graph with AB separation = BC separation = 0.91 Angstrom, with much less oscillation in the separation, but inversion of the oscillation compared to Figure 2, indicating optimum TS distance has been exceeded

Figure 4 - Internuclear Separation against time showing extrememly minimal oscillation, hence the optimal distance for AB and BC separation in the TS has been found.

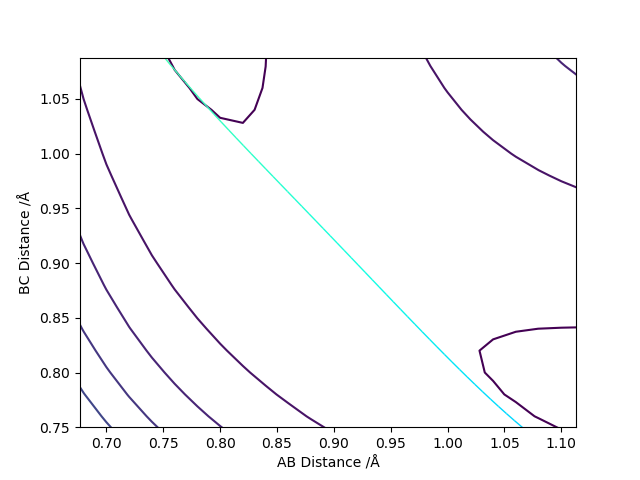
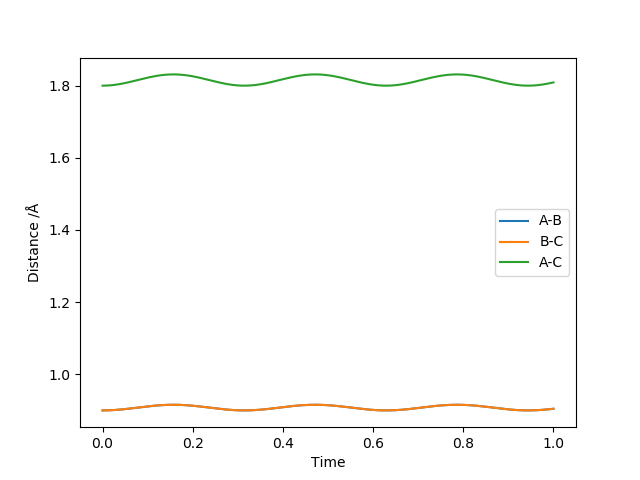
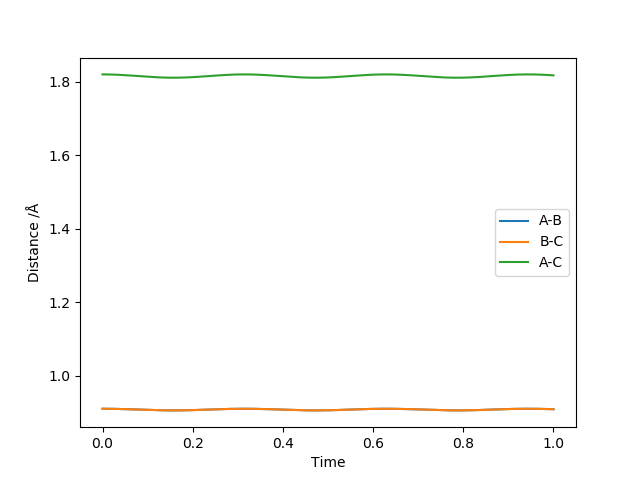
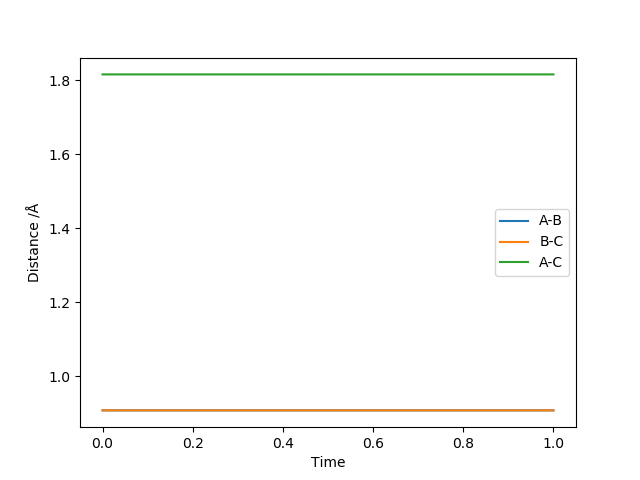
Figure 4 shows a good estimate for AB separation = BC separation = 0.9079 Angstrom.

Question 3

Comment on how the MEP and trajectory you just calculated differː

Figure 5 - Contour plot showing the minimum energy pathway under an MEP calculation type, with step number increased

Figure 6 - Contour plot showing the reaction pathway with the same reaction conditions that generate the MEP under a dynamic calculation type

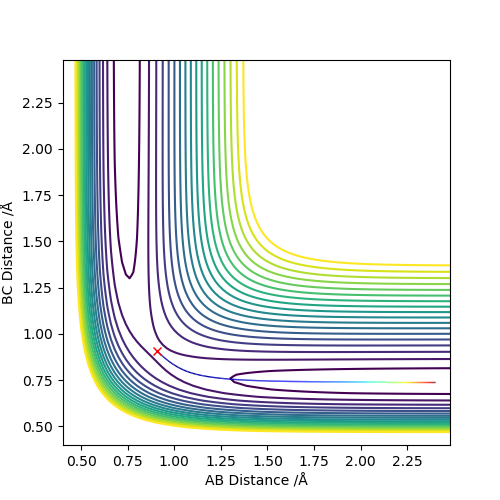
The minimum energy pathway shows that there is no energy stored in the vibrational modes of the BC bond because there is no oscillation of the pathway along the BC axis. Under the dynamic calculation type there is an oscillation of the B-C bond and hence an oscillation along this axis which means that this trajectory does not follow that of the minimum energy pathway. This trajectory is also more accurate of the actual reaction pathway the reaction proceeds by as it is highly unlikely the B-C bond is rigid.

Does the MEP even yield a physical trajectory?Fdp18 (talk) 20:51, 11 May 2019 (BST)

Question 4

Sim Number	p1	p2	Etot	Reactive	Description
1	-1.25	-2.50	-99	Yes	H2 approaches the H atom, the H-H bonds breaks, and a new H-H bond forms with the lone atom
2	-1.50	-2.00	-100	No	H2 approaches the H atom, H-H bond starts to increase in length but doesn't break.
3	-1.50	-2.50	-99	Yes	H2 approaches the H atom, H-H bond bond breaks and a new H-H bond forms with the lone atom. So is there no difference to 1? It is also similar to 2, so why does it react? Fdp18 (talk) 20:55, 11 May 2019 (BST)
4	-2.50	-5.00	-85	No	The H-H bond breaks, and a new H-H bond forms with too much vibrational energy, so it breaks too and the original H-H bond reforms.
5	-2.50	-5.20	-83	Yes	The H-H bond breaks, and a new H-H bond forms with too much vibrational energy, so it breaks too and the original H-H bond reforms, before this bond has too much vibrational energy and breaks and the other H-H bond forms making the reaction reactive.

Figure 7 - Shows the trajectory from reactive Sim 1

Figure 8 - Shows the trajectory from unreactive Sim 2

Figure 9 - Shows the trajectory from reactive Sim 3

Figure 10 - Shows the trajectory from unreactive Sim 4

Figure 11 - Shows the trajectory from reactive Sim 5

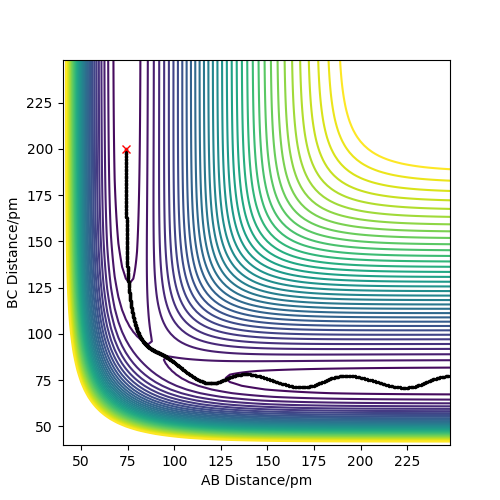
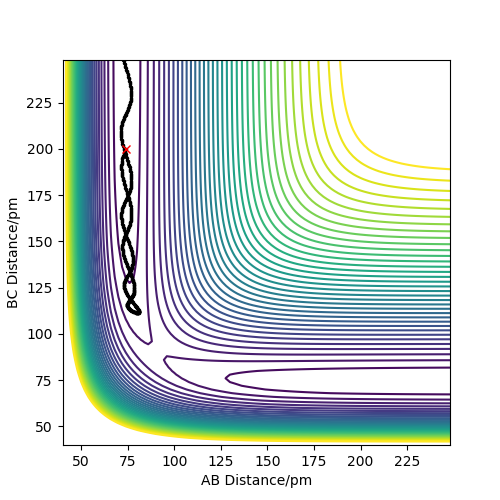
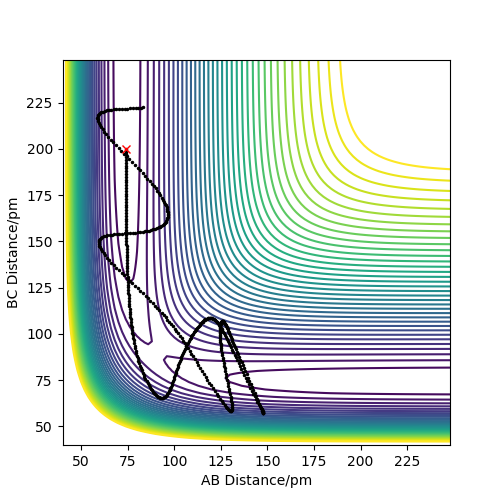
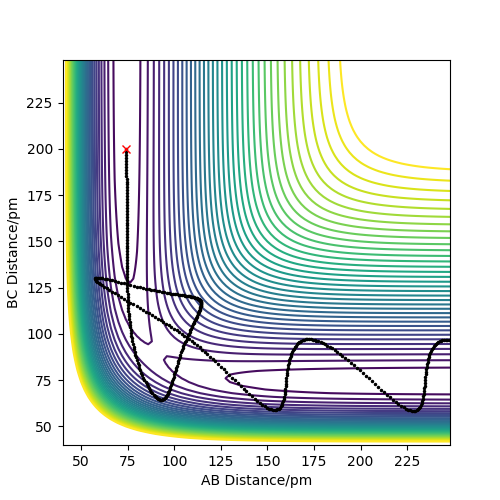
In conclusion this means that the hypothesis stated is not true as Sim 5 shows a reactive simulation where p₁=-2.5 and p₂=-5.2. These momenta lie outside the range stated in the hypothesis, therefore it is not true.

I couldn't find the hypothesis you are talking about. If something is not mentioned in your report, provide a reference. This includes the script... If it is mentioned later, it is nice to include a note like 'the hypothesis given in chapter xx..' to help the reader. Fdp18 (talk) 20:58, 11 May 2019 (BST)

Question 5

Transition state theory assumes that the atoms in the reactant state all have energies that follow the Boltzmann distribution and it also assumes that quantum tunnelling effects are negligible and the Born-Oppenheimer approximation is applied. A second assumption is that the products can not go back to the reactants after passing through the transition state.

This means that for the simulations 1,3,4 and 5, rate constants can only be obtained using for the forwards reactions in simulations 1 and 3 as these do not revert back to the reactants. For reactions 4 and 5, the rate constant determined by experiment will not be in agreement with that calculated for using the transition state theory as the reaction passes back through the transition state, hence transition state theory is not valid here.

In which way will experiment and transition state theory differ? Will one of them be consistently yield higher rate constants, or will the difference be random? Fdp18 (talk) 21:03, 11 May 2019 (BST)

I am very much missing the reference you used for TST. Fdp18 (talk) 21:04, 11 May 2019 (BST)

Exercise 2

Question 1

The reaction HF + H → H₂ + F is endothermic as the products have a higher energy than the reactants. The reverse reaction H₂ + F → HF + H is therefore exothermic as the products are lower in energy than the reactants as shown in Figure 1.

Figure 1 - Potential energy curve for the reaction HF + H → H₂ + F Nice picture.Fdp18 (talk) 21:06, 11 May 2019 (BST)

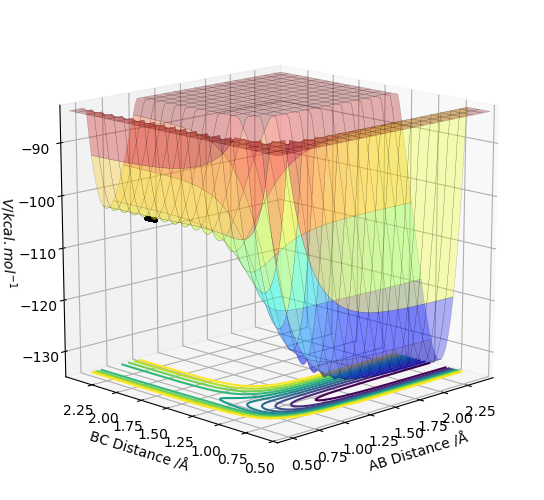
This is to be expected as the H-H bond energy = 432 kJ mol^-1, whereas the H-F bond energy = 565 kJ mol^-1.¹ The H-F bond is stronger than the H-H bond, so in the first reaction HF + H → H₂ + F, this explains why the reactants are lower in energy than the reactants and explains why the products are lower in energy than the reactants in the second reaction H₂ + F → HF + H.

Reference: 1) 1 E. Lippert, Angew. Chemie, 1960, 72, 602.

It is possible to include dynamically linked references in your wiki. Fdp18 (talk) 21:08, 11 May 2019 (BST)

Question 2

The transition state corresponds to the saddle point on the curve, which can be approximated to be at the position along the curve where r_HH = 0.745 Angstrom and r_HF = 1.811 Angstrom. At these distances, the internuclear separation is constant between H-H and H-F, so the transition state is achieved.

Figure 2 - Plot of Internuclear separation over time, which is constant between all nuclei so the transition state has been achieved.

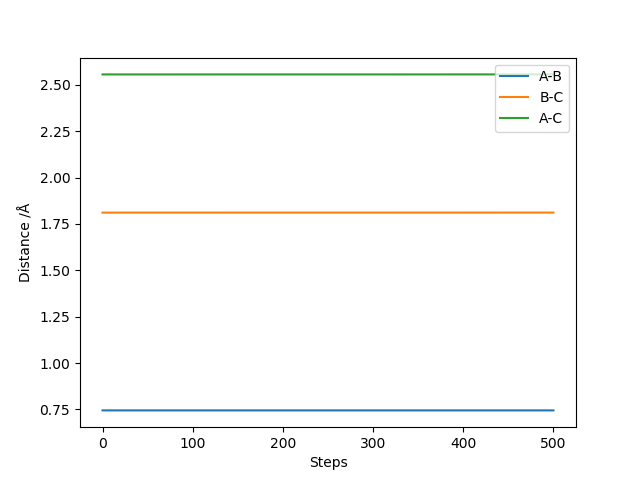
Question 3

Hammond's postulate states that the transition state of a reaction will closely match the reactants or products depending on which is closer in energy. This means that the transition state in this case resembles the reactants H₂ + F more than the products HF + F since the transitions state energy is similar to that of the products. By slightly changing the structure of transition state as such that its energy now lies slightly away from the transition state energy, but still closely resembles H₂ + F, the activation energy for both reactions can be approximated by measuring the energy difference between this point on the potential energy curve and the energy of the products for each reaction on the same curve.

Figure 3 - Shows the activation energy as the change in energy from t = 0s to t = 7s

The calculated activation energy for the reaction H₂ + F → HF + F was 0.150 kJ mol^-1.

Figure 4 - Shows the activation energy as the change in energy from t = 0s to t = 7s

The calculated activation energy for the reaction HF + F → H₂ + F was 30.187 kJ mol^-1.

Question 4

The reaction conditions of r_HH = 0.8, r_HF = 2.0, p_HH = -3 and p_HH = -1 leads to a reactive trajectory. From the animation, the H-F bond that forms contains lots of energy in the vibrational mode which suggests that the energy released from the reaction goes into this vibrational mode. The large increase in the amplitude of oscillation increases both the potential energy and kinetic energy of the system accordingly so the total energy of the system remains the same. The average kinetic energy of the system increases, which means that the temperate of the system will increase according to $<E>=0.5k_{B}T$ for a 1D gas. Hence, the best way to monitor this release of reaction energy is to measure the temperature over the course of the reaction.

It's not really a 1D gas, the product can translate (3 degrees of freedom) and rotate (2 degrees of freedom). Vibration (another degree of freedom) makes it a bit more complicated. Nevertheless, you got a point there, and I like that you used the Equipartition theorem. Fdp18 (talk) 21:29, 11 May 2019 (BST)

The energy stored in the vibration of HF can even be used for an IR LASER by combining fluorine radicals with H₂.Fdp18 (talk) 21:32, 11 May 2019 (BST)

Figure 5 - Shows the variation in kinetic and potential energy over time for the reaction and shows that the average kinetic energy increases after the reaction has taken place.

Question 5

For r_HH = 0.74 and r_HF = 1.5, several trajectories were plotted corresponding to different momenta of the F particle and the H-H bond.

Sim Number	pHH	pHF	Reactive	Description
1	-3	-0.5	No	H-H bond breaks, and the H-F bond forms which oscillates and breaks and reforms the original H-H bond
2	-3	-1.5	Yes	H-H bond breaks and H-F bond forms, but this breaks and H-H reforms again which then breaks and H-F forms and continues to oscillate with large amplitude but doesn't break.
3	-3	-0.50	Yes	H-H bond breaks, and H-F bond forms which oscillates with large amplitude.
4	-3	0	Yes	The H-H bond breaks and H-F forms which oscillates with large amplitude
5	-3	0.5	Yes	The H-H bond breaks and H-F forms which oscillates with large amplitude
6	-3	1.5	Yes	The H-H bond breaks and H-F forms which oscillates with large amplitude causing it to break and the H-H bond reforms which the oscillates and breaks causing H-F to reform.
7	-3	3	Yes	H-H bond breaks, H-F forms which oscillates with large amplitude and H-H reforms, which oscillates 3 times before breaking and reforming H-F permanently.

General conclusionsː

For the reaction between H₂ and F, as the momentum in the H-H bond increased, the faster it broke and the faster the H-F bond formed, however the H-F bond would then oscillate with such a large amplitude the bond would break. When the momenta in this bond was slower, the H-F bond would form slower and would still oscillate with large amplitude, but would not break. The energy released from the reaction goes in to H-F bond meaning the products do not have enough potential energy to revert back over the transition state and reform the reactants. This means that the reaction is more efficient at lower momenta in the H-H bond. For the reaction to not revert back to the reactants the activation energy for the reverse reaction must not be exceeded which is achieved when there is a lot of kinetic energy in the products and a small H-F vibration. A small H-F vibration is achieved by having minimal energy greater than the activation energy for the initial reactants.

For the reverse reaction between HF and H, the higher the kinetic energy of the H atom, the less likely a reaction is to occur successfully. At high kinetic energies, the H atom rebounds straight back out after the collision and no reaction occurs. The H atom has so much kinetic energy which is transferred to the H-H vibrational mode. This energy is so large that the H-H molecule can pass back over the transition state and reform the reactants. This means the reaction is successful when the kinetic energy lower of the H atom is lower and the kinetic energy is more evenly distributed throughout the system. Since the activation energy for the reverse reaction in this case is so small, the amount of energy required to overcome the transition state initially without having enough to revert back over it is very specific. This means that the position of the transition state affects the efficiency of the reaction as such a specific amount is required which doesn't allow the reactants to reform.

The question was aiming at the Bell-Evans-Polanyi principle well known from organic chemistry. However, I like your discussion more since you put your own thoughts in it. After all you should learn how to think for yourself, not to just produce data. Fdp18 (talk) 21:38, 11 May 2019 (BST)

here the reference section. Fdp18 (talk) 21:11, 11 May 2019 (BST)