Molecular Dynamics report

Exercise 1: H + H₂ system

Dynamics from the transition state region

Mathematical definition of the transition state

The transition state is defined as being a saddle point in the surface plot of the reaction. That is, it is a minimum with respect to one coordinate and a maximum with respect to the others.

$\frac{\partial V}{\partial r_{1}} = \frac{\partial V}{\partial r_{2}} = 0$ and $\frac{\partial^{2} V}{\partial {r_{1}}^{2}} < 0$ , $\frac{\partial^{2} V}{\partial {r_{2}}^{2}} > 0$ where r₁ and r₂ can be interchanged.

Distinguishing it from a local minimum

To distinguish the transition state from a local minimum, one must check all coordinates. For a local minimum, it could be that the point is a minimum with respect to the other coordinate as well. The condition to be met is that the second derivatives of potential must be of opposite sign for both coordinates.

I think you mean direction not coordinate. Also, you should talk about orthogonal directions being maxima and minima on a TS point, not just two directions because there isn't just one direction where there is a minimum as if you turn the direction slightly there will still be a minimum, i.e the minimum isn't on an infinitely thin line. Otherwise this answer is all correct. Pu12 (talk) 14:53, 23 May 2019 (BST)

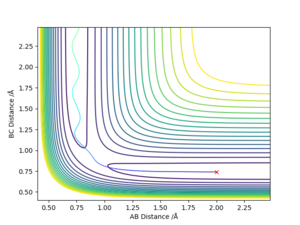
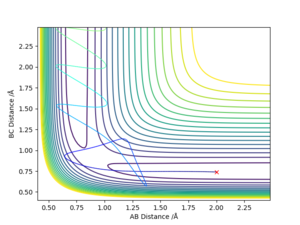
Estimation of the transition state position

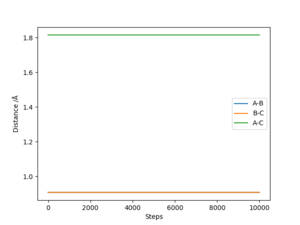
The transition state was estimated to have a position of r₁= r₂ = 0.908 Å.

To determine it, the contour plot was first examined to find the region with lowest potential. Then, the internuclear distances against time plot was used as it is known that for the transition state, the internuclear distances must stay constant: no slope in the plot, and minimal variations due to vibrations. Thus after obtaining an initial guess with the contour plot, the value was more accurately determined by trial and error using the internuclear distances against time plot.

For the example reaction of H + H₂ we have:

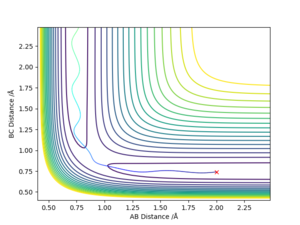
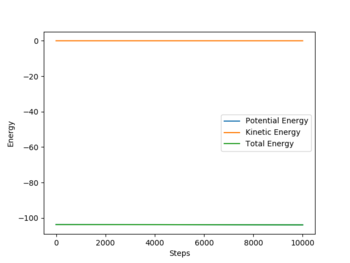
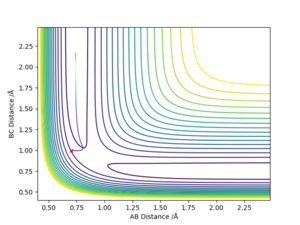
Differences between the mep and dynamics trajectories

The main difference between the two types of calculations is that mep, because it wants to provide the shortest path possible, doesn't take into account the possible vibrations of the molecules. The reason why mep produces a straight line is that it resets the momentum to zero after each step of the calculation.

good. Pu12 (talk) 14:53, 23 May 2019 (BST)

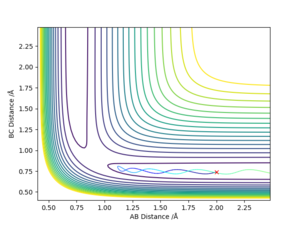
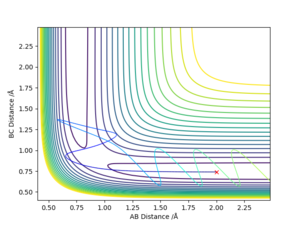
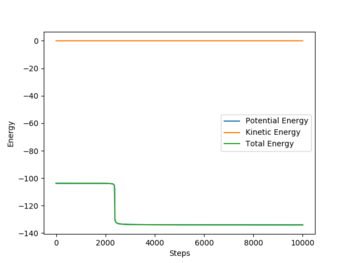
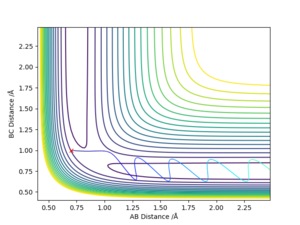
Reactive and unreactive trajectories

p₁	p₂	E_tot	Reactive?	Description of the dynamics
-1.25	-2.5	-99.119	yes	Incoming atom approaches slowly, then atoms stay for a while in a "transition state like" situation with left and right atoms at equal distances from central atom, and finally the molecule is formed and leaves towards the left
-1.5	-2.0	-100.456	no	Incoming atom approaches H₂ molecule, stays close to it for a second or two and then leaves where it came from
-1.5	-2.5	-98.956	yes	Incoming atom approaches H₂ molecule, and when it it close enough, the central atom moves towards it and forms the molecule than leaves to the left
-2.5	-5.0	-84.956	no	Incoming atom approaches molecule, and at first central atom moves towards incoming atom. It seems that a molecule was formed but it vibrates twice before the central atom goes back with the atom it initially formed a molecule with
-2.5	-5.2	-83.416	yes	As the incoming atoms approaches the initial molecule, it seems that it forms a molecule with the central atom. This vibrates once, and then the central atom goes back to form the inital molecule, which vibrates once as well. Eventually, the central atom forms a new molecule with the incoming atom and slowly leaves to the left

good, but should include discussion of vibration for each graph. Pu12 (talk) 14:53, 23 May 2019 (BST)

This data reflects the importance of initial momenta: even if there is enough energy to overcome the activation energy, it is not certain that the reaction will be successful.

Transition State Theory

According to Bligaard and Nørskov^[1], the main assumptions of transition state theory are that: - quantum-tunnelling effects are negligible - the Born-Oppenheimer approximation is applied - an incoming flux of reactants should be thermally equilibrated - once the system/reaction reaches the transition state with a velocity towards the products side, it will not go back to the initial state So how would using these assumptions compare to the results that you have just reported, regarding rate? Pu12 (talk) 14:53, 23 May 2019 (BST)

Exercise 2: F-H-H system

In this exercise, r₁ refers to r_FH -the distance between the F atom and the H atom-, and r₂ refers to r_HH - the distance between the two H atoms-. Energies are in kcal/mol.

PES inspection

Classification of the F + H₂ and HF + H reactions

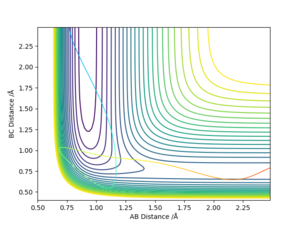
The energetics of the reaction can be determined by looking at the surface plot.

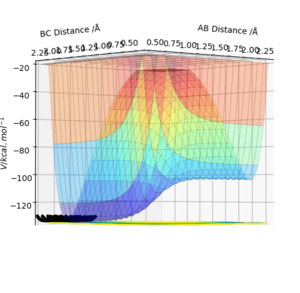
It can be seen that it takes up energy to go towards F + H₂ and energy is gained going towards HF + H. The first reaction is endothermic, the latter is exothermic.

This explanation is confusing, what is the first reaction? The one that is first in the question F +H2-> HF + H or the first reaction that you have said that's "going towards F + H2", please be more clear in the future. It looks like you mean the latter and that HF + H -> F+ H2 is endothermic as it requires an input of energy, this is correct well done. Pu12 (talk) 14:53, 23 May 2019 (BST)

Using the contour plots of the reaction, computed using the mep method, by looking at both ends of the reaction, the experimental bond lengths of H-F and H-H could be determined. It was found that H-F = 0.920 Å, and H-H= 0.741 Å.

The energetics of the reactions reflect the fact that the HF bond is stronger than the H₂ bond, as it is more favourable energetically to form HF because it is a stronger and more stable bond.

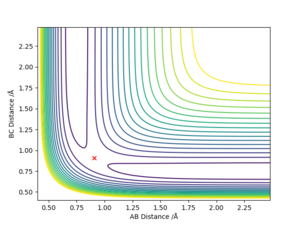
Location of the transition state positions

The position of transition state was found using three types of plots: the surface plot, the contour plot of the reaction and the Internuclear Distances vs Time plot. The first one was used to obtain a rough first guess of the location of the transition state by examining where the saddle point of the plot could be. Next, the internuclear distances against time plot was used when adjusting the values of our initial guess. The transition state would have as a condition that all distances stay constant: that means no slopes and minimal vibrations. Finally, the guesses were further checked by looking at the contour plot: if the set distances were those of the position of the transition state, giving atoms no momenta, then there would be no trajectory.

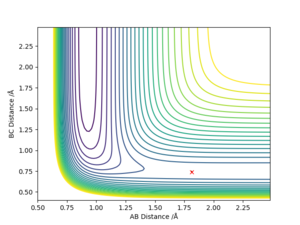
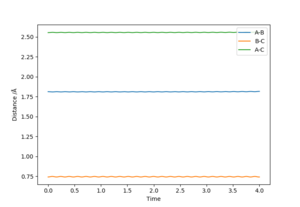
Thus, the position of the transition state for the reaction is r₁=1.81263 Å and r₂= 0.74150 Å.

Activation energies of the reactions

The activation energy is defined as the difference between the energy of the reactants and the transition state. Using a plot of energy against time, the difference in energy between the end and the beginning of a reaction was determined. In this case, the starting position was slightly offset compared to the transition state and towards the reactants side.

For the F + H₂ reaction: E_a= 103.912 - 103.748 = 0.164 kcal/mol

For the HF + H reaction: E_a= 133.975- 103.914 = 30.061 kcal/mol

All good. Pu12 (talk) 14:53, 23 May 2019 (BST)

Reaction dynamics

Mechanism of release of the reaction energy

F + H₂

A set of reactive conditions is r₁ = 2, r₂ = 0.8, p₁=-4 and p₂=0.6, with a total energy of -91.395 kcal/mol.

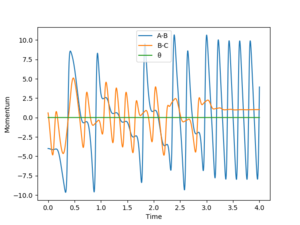
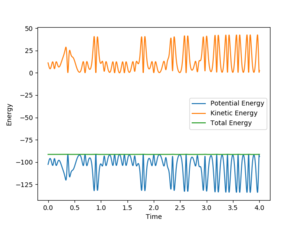
From these plots it can be seen that momentum increases overall through time, and that the kinetic energy contribution to the total energy also increases over time. That means that potential energy is being converted to kinetic energy. The latter goes either into motion of particles or vibrations: through that we eventually obtain thermal energy.

To investigate on the mechanism, a possible way would be to use calorimetry and measure the increase of temperature -when forming HF-, or decrease -when forming H₂.

p_HH	E_tot	Reactive?	Description of the dynamics
-3	-96.159	no	The F atom approaches the molecule which seems to dissociate at one point but ends up leaving where it came from
-2.9	-96.699	no	The F atoms collides with the hydrogen molecule four times but the initial molecule leaves where it came from
-2.8	-97.219	no	The F atoms collides with the hydrogen molecule two times but the initial molecule ends up leaving where it came from
-2.7	-97.719	yes	The F atom has to collide two times with the hydrogen molecule before the HF molecule is formed
-2.6	-98.199	no	The F atom collides once but the initial hydrogen molecule ends up leaving from where it came from
-2.5	-98.659	no	The F atom collides once but the initial hydrogen molecule ends up leaving from where it came from
-2	-100.659	yes	The F atom has to collide once with the hydrogen molecule before the HF molecule is formed
-1.5	-102.159	yes	The F atom has to collide three times with the hydrogen molecule before the HF molecule is formed
-1	-103.159	yes	The F atom has to collide two times with the hydrogen molecule before the HF molecule is formed
0	-103.659	yes	The F atom has to collide three times with the hydrogen molecule before the HF molecule is formed
1	-102.159	no	The F atom collides twice but the initial hydrogen molecule ends up leaving from where it came from
1.5	-100.659	yes	The F atom has to collide once with the hydrogen molecule before the HF molecule is formed
2	-98.659	no	The F atom collides once but the initial hydrogen molecule ends up leaving from where it came from
2.5	-96.159	no	The F atom collides once but the initial hydrogen molecule ends up leaving from where it came from
2.6	-95.599	no	The F atom collides once but the initial hydrogen molecule ends up leaving from where it came from
2.7	-95.019	no	The F atom collides thrice but the initial hydrogen molecule ends up leaving from where it came from
2.8	-94.419	yes	The F atom has to collide nine times with the hydrogen molecule before the HF molecule is formed
2.9	-93.799	yes	The F atom has to collide twice with the hydrogen molecule before the HF molecule is formed
3	-93.159	no	The F atom collides once but the initial hydrogen molecule ends up leaving from where it came from

HF + H

The set of initial conditions chosen are: r₁=0.9, r₂=2, p₁=-5, p₂=,-18

By slowly decreasing the momentum of the incoming H atom, we obtain a reactive situation when p₂ =-12.

The Polanyi rules^[2] imply that vibrational energy is more efficient when it comes to promoting a late-barrier reaction compared to translation energy.

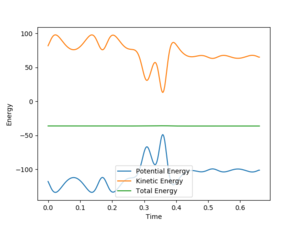
From the plots we can see that at the start of the reaction (HF +F) we store more energy in vibration in the HF bond than we do at the end of the reaction (F + HH) in the HH bond. Is your reaction late barrier or early barrier? You imply this, but again, please be more clear in your explanations as a full answer is required. Pu12 (talk) 14:53, 23 May 2019 (BST)

This is a good report but some answers miss out parts. Pu12 (talk) 14:55, 23 May 2019 (BST)

↑ https://www.sciencedirect.com/topics/chemistry/transition-state-theory
↑ https://pubs.acs.org/doi/10.1021/jz301649w

[1] ttps://www.sciencedirect.com/topics/chemistry/transition-state-theory

[2] ttps://pubs.acs.org/doi/10.1021/jz301649w

[1]

[2]