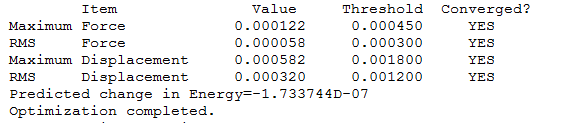CCL:lydia
BH3 Molecule
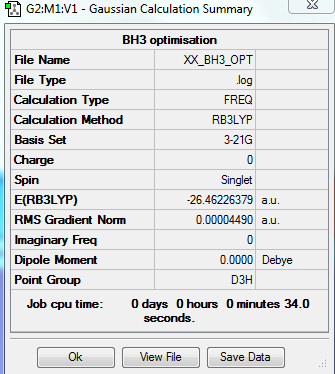
Basis set 3-21G and Calculation method RB3LYP
Summary table
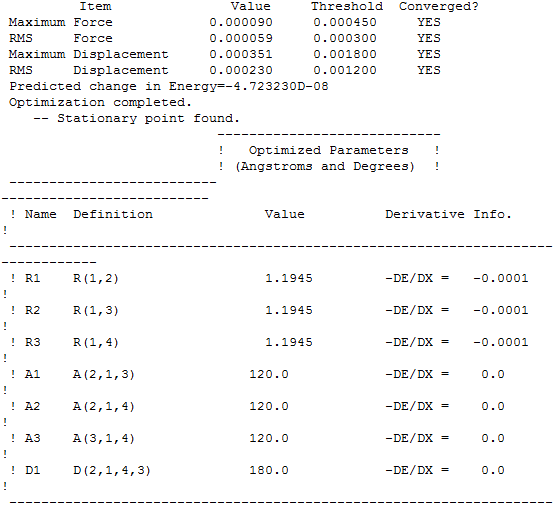
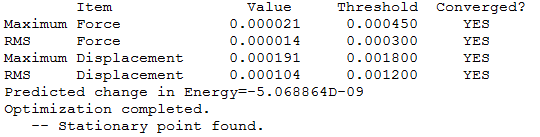
Item table
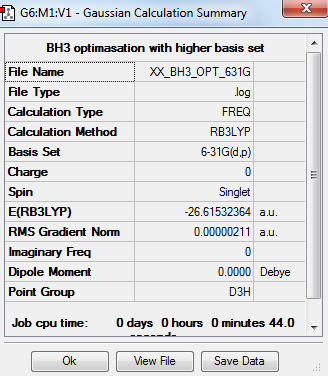
Basis set 6-31G and Calculation method RB3LYP
Summary Table
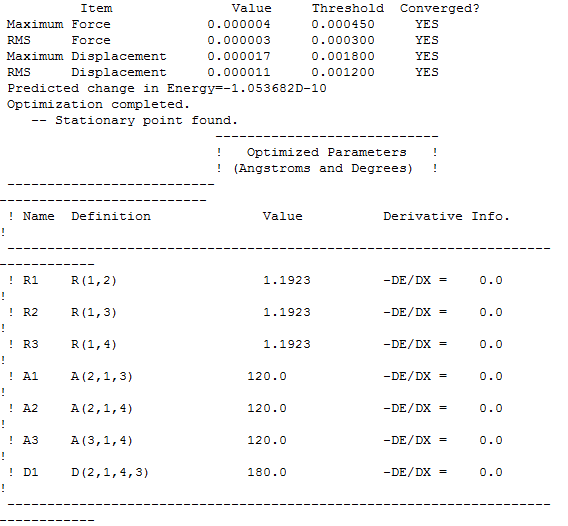
Item Table
BH3 frequency
Frequency File: File:XX BH3 FREQ.LOG
The convergence of low frequency values are within the +/-15 region, thus the frequency analysis is complete.
BH3 molecule |
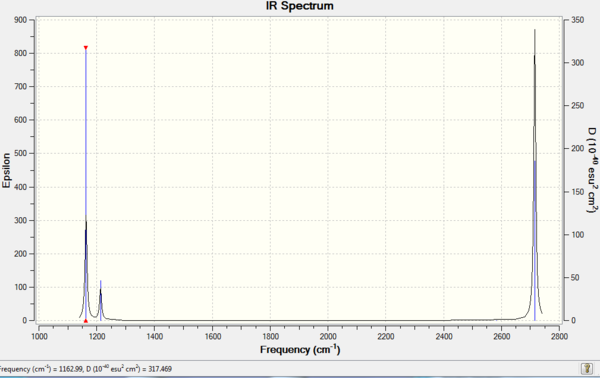
Vibrational spectrum of BH3 molecule
| Frequency | IR intensity | Symmetry | IR Active | type |
|---|---|---|---|---|
| 1162.97 | 92.5682 | A2 | Yes | out-of-plane bend |
| 1213.14 | 14.0550 | E | Slightly | bend |
| 1213.14 | 14.0544 | E | Slightly | bend |
| 2582.58 | 0.0000 | A1 | No | Symmetric stretch |
| 2715.72 | 126.3320 | E | Yes | Asymmetric stretch |
| 2715.72 | 126.3260 | E | Yes | Asymmetric stretch |
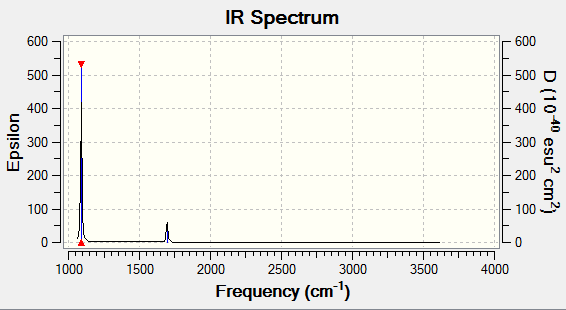
The vibrational spectrum of BH3 molecule is shown below. Six peaks are expected to see with each corresponding to one vibrational mode. However, only three peaks can be seen on the spectrum. The two bend peaks have the same fequency, which lead to the two peaks are present as a whole, same for the two peak correspond to asymmetric streches (same frequency). The symmetric stretch is not IR active since there is no dipole change upon vibration, thus there is no peak on IR spectrum.
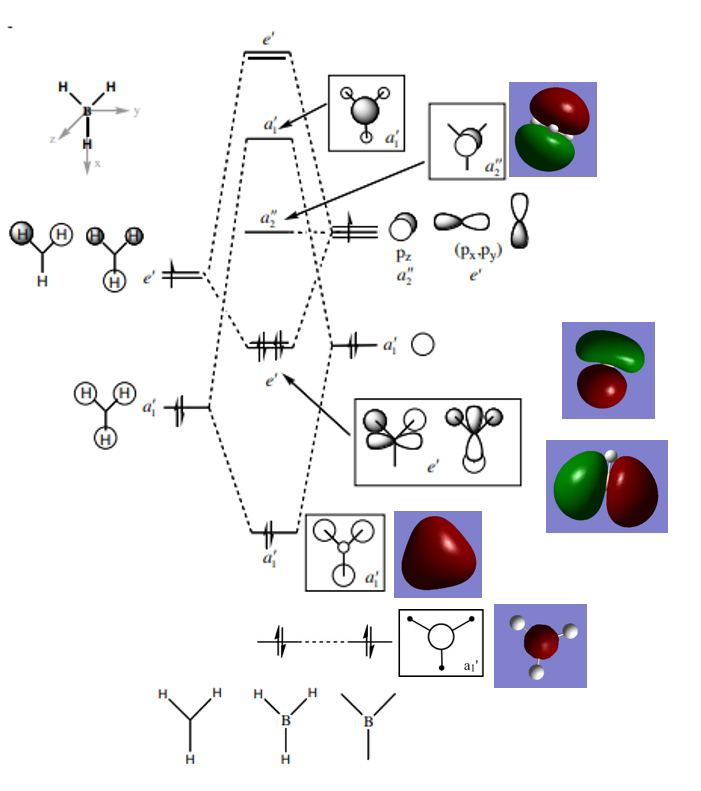
BH3 MO diagram
Ng611 (talk) 16:31, 22 May 2018 (BST) Remember to include the antibonding MOs in your diagram too.
The above figure shows a BH3 MO diagram [1] with real MO orbitals (the occupied MOs and the LUMO). As shown in the figure, the real MOs look really similar to the LCAO MOs, they have similar in-phase region and out-of-phase region. This proves that the qualitative MO theory is quite accurate and useful in predicting the shape of the MOs.
Ng611 (talk) 16:31, 22 May 2018 (BST) From comparing the calculated and qualitative MOs, are there any differences at all between them, and what does this tell you about qualitative MO theory?
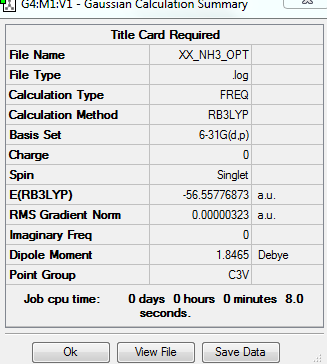
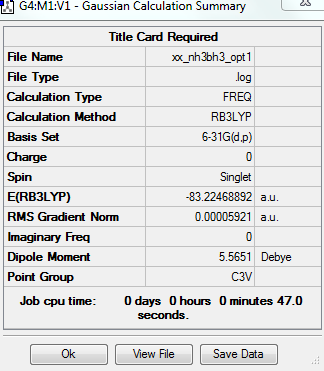
NH3 molecule
Basis set and calculation method
Optimisation of the NH3 molecule uses basis set of 6-31G (d,p) and calculation method of RB3LYP.
Summary table
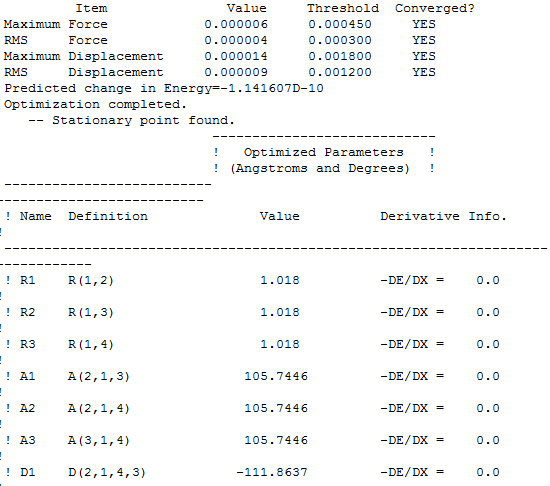
Item table
Frequency optimisation of NH3 molecule
Frequency File: File:XX NH3 FREQ.LOG
The low frequency values are outside the +/-15 region. However, for NH3, the formally zero frequencies are well separated from the lowest energy positive frequency at 1088cm-1 and the large formally zero frequencies are due to the low level of the basis set and relatively relaxed convergence and integration criteria.
NH3 molecule |
Vibrational spectrum of NH3 molecule
| Frequency | IR intensity | Symmetry | IR Active | type |
|---|---|---|---|---|
| 1088.76 | 145.4214 | A1 | Yes | out-of-plane bend |
| 1694.19 | 13.5548 | E | Slightly | bend |
| 1694.19 | 13.5549 | E | Slightly | bend |
| 3461.00 | 1.0598 | A1 | No | Symmetric stretch |
| 3589.74 | 0.2708 | E | No | Asymmetric stretch |
| 3589.47 | 0.2709 | E | No | Asymmetric stretch |
The vibrational spectrum of NH3 molecule is shown below. Six peaks are expected to see with each corresponding to one vibrational mode. However, there are only two [eaks shown on the spectrum.
Molecular vibrations of symmetric stretch and asymmetric stretch only create a small dipole change, thus, the IR intensity is negligible and the peaks not shown in the IR spectrum.
The two bent vibrations give the same IR frequency, therefore, shown as a single pak on the IR spectrum.
NH3BH3 molecule
Basis set and calculation method
Optimisation of the NH3BH3molecule uses basis set of 6-31G (d,p) and calculation method of RB3LYP.
Summary table
Item table
Frequency optimisation of NH3BH3 molecule
Frequency File: File:XX NH3BH3 FREQ.LOG
The low frequency values are within the +/-50 region. Thus, the optimisation is complete.
NH3BH3 molecule |
Association Energy
| Molecule | Energy in au | Energy in kJmol-1 |
|---|---|---|
| NH3 | -56.558au | -35.49*103kJmol-1 |
| BH3 | -26.462au | -16.60*103kJmol-1 |
| NH3BH3 | -83.225au | -52.22*103kJmol-1 |
Ng611 (talk) 16:33, 22 May 2018 (BST) Your accuracy here is a bit too coarse. You needed to go to 5 decimal places, rather than 3.
ΔE=E(NH3BH3)-[E(NH3)+E(BH3)]= -130kJmol-1
Therefore, the bond energy of the N-B bond is 130kJmol-1, which indicate the bond being a fairly weak bond compare to the bond energy of the C-C single bond with medium bond energy (348kJmol-1).
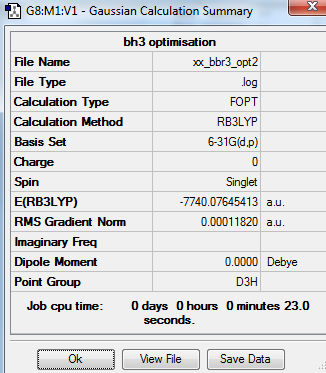
BBr3 molecule
Basis set and calculation method
The optimisation of BBr3 molecule uses calculation method of B3LYP and basis set of GEM. The frequency optimisation of BBr3 molecule uses calculation method of B3LYP and basis set pf 6-31G(d,p).
Summary table
Item table
Frequency optimisation of BBr3 molecule
Frequency File: File:XX BBR3 FREQ.LOG
The low frequency values are within the +/-15 region. Thus, the optimisation is complete.
BBr3 molecule |
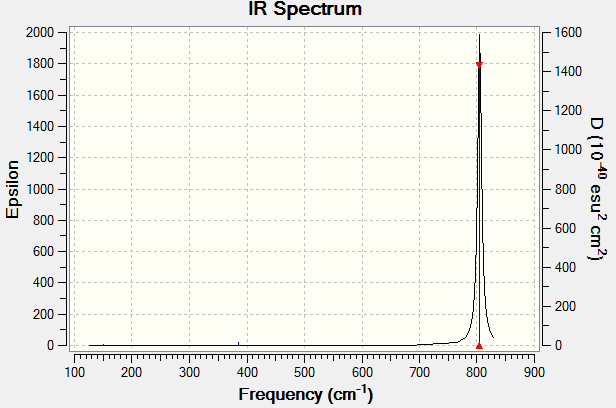
Vibrational spectrum of BBr3 molecule
| Frequency | IR intensity | Symmetry | IR Active | type |
|---|---|---|---|---|
| 150.82 | 0.1354 | E | No | bend |
| 150.82 | 0.1354 | E | No | bend |
| 279.84 | 0.0000 | A1 | No | Symmetric stretch |
| 385.14 | 1.4146 | A2 | No | out-of-plane bend |
| 804.59 | 288.4456 | E | Yes | Asymmetric stretch |
| 804.63 | 288.4458 | E | Yes | Asymmetric stretch |
The below figure is an image of the spectrum of the BBr3. Six peaks are expected to see since there are six vibrational modes. However, there is only one peak on the spectrum. This is due to that there is no dipole change on the molecule upon bend, symmetric stretch and out-of-plane bend, thus the vibrations are IR inactive.
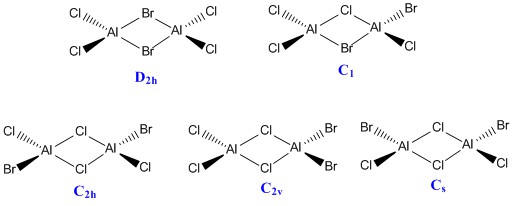
Al2Cl4Br2 molecule
Isomers and point group
Ng611 (talk) 16:34, 22 May 2018 (BST) Your final isomer is should acutally also be C2V, not CS
Isomer 1 with Br as bridging molecules
Basis set and calculation method
Optimisation of the Al2Cl4Br2 molecule uses basis set of GEN and calculation method of RB3LYP.
Summary table
Item table
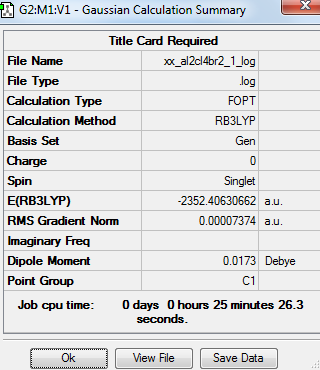
Frequency optimisation of Al2Cl4Br2 molecule
Frequency log file: File:XX AL2CL4BR2 1 FREQ.LOG
The convergence of the low frequency values are within the +/-15 region. Thus, the optimisation is complete.
Isomer 1 with Br as bridging molecules |
Isomer 2 with Cl as bridging molecules
Basis set and calculation method
Optimisation of the Al2Cl4Br2 molecule uses basis set of GEN and calculation method of RB3LYP.
Summary table
Item table
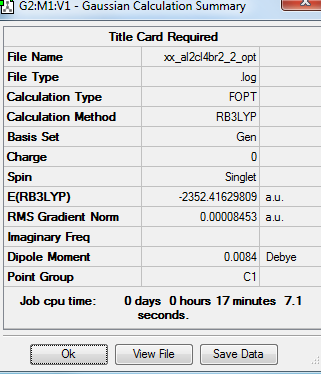
Frequency optimisation of Al2Cl4Br2 molecule
Frequency File: File:XX AL2CL4BR2 2 FREQ.LOG
The convergence of the low frequency values are within the +/-15 region. Thus, the optimisation is complete.
isomer 2 with Cl as bridging molecule and Br trans |
AlCl2Br
Basis set and Calculation method
Optimisation of the AlCl2Br molecule uses basis set of 6-31G (d,p) and calculation method of RB3LYP.
Summary table
Item table
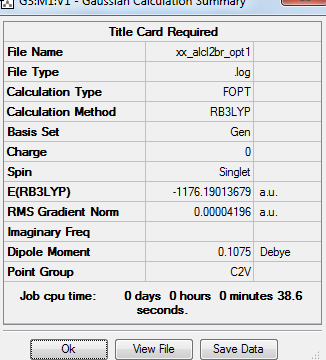
Frequency optimisation of AlCl2Br
Frequency File: File:XX ALCL2BR FREQ.LOG
The convergence of the low frequency values are within the +/-15 region, thus the optimisation is complete.
AlCl2Br molecule |
Energy comparision of the two isomers
Energies of the two isomers
| Molecule | Energy in au | Energy in kJmol-1 |
|---|---|---|
| isomer 1 | -2352.406au | -1.476134*106kJmol-1 |
| isomer 2 | -2352.416au | -1.476141*106kJmol-1 |
Relative energy = E(isomer 1)-E(isomer 2) = -2352.406au + 2352.416au = 0.010au = 6.275kJmol-1 The energy of isomer 2 is slightly lower than the energy of isomer 1. Isomer 2 uses Chloride atom as the bridging atom. the Cl and Al are in the same period in the periodic table, thus their sizes matches more than Br and Al. Therefore, the orbital overlap of Cl and Al is larger, giving rise to lower energy of the isomer.
Ng611 (talk) 16:38, 22 May 2018 (BST) Correct energies and good calculation giving the correct result in a.u. although your conversion to kJ/mol is incorrect. Remember also to report your final value to the nearest Kj/mol.
Dissociation energy for the lowest energy conformer into 2AlCl2Br
| Molecule | Energy in au | Energy in kJmol-1 |
|---|---|---|
| isomer 2 | -2352.416au | -1.476141*106kJmol-1 |
| AlCl2Br | -1176.190au | -7.38*105kJmol-1 |
ΔE=2E(AlCl2Br)-E(Al2Cl4Br2)= 1.41*10-3kJmol-1kJmol-1
the product is much more unstable than the divalent metal complex since the Al atom in the monomer is largely electron deficient and it experience no electron donation from the bridging atom.
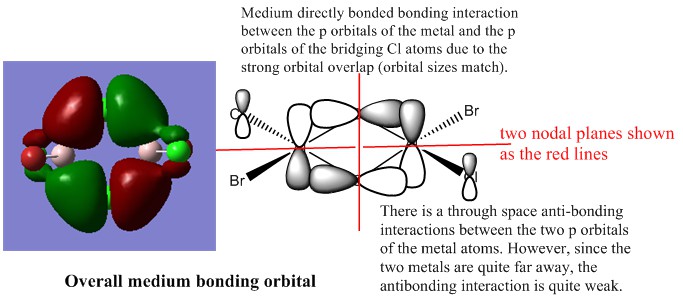
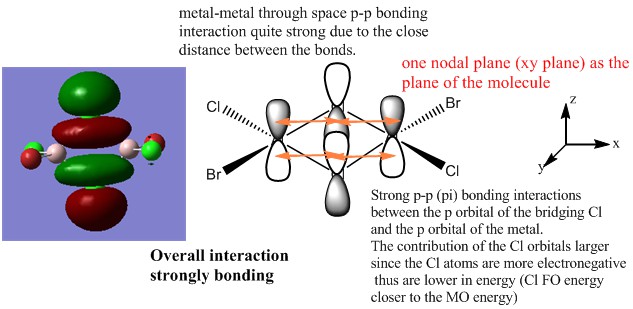
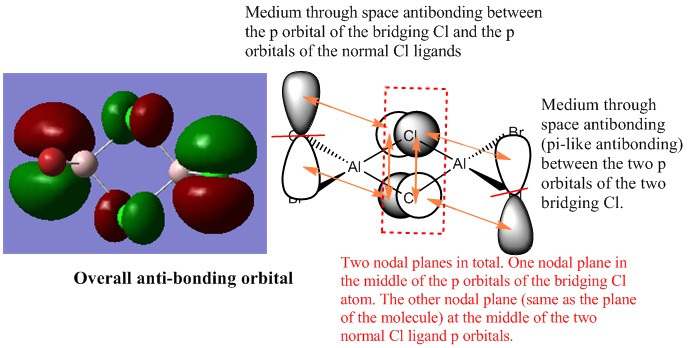
MOs of the lowest energy conformer
Below are the bonding and antibonding analysis on three MOS of the isomer with Cl as the bridging atoms and the Br atoms in trans positions.
The first occupied MO of overall bonding interactions
The second occupied MO of overall bonding interactions
The third occupied MO of overall anti-bonding interactions
References
- ↑ Patricia Hunt, HuntResearchGroup, http://www.huntresearchgroup.org.uk/teaching/teaching_comp_lab_year2a/Tut_MO_diagram_BH3.pdf, Accessed 16/05/2018
Ng611 (talk) 16:44, 22 May 2018 (BST) A good report overall. Take care when performing your energy difference calculations and especially when reporting your final answer to the correct degree of accuracy. Otherwise, your calculations were correct and your results were good - well done.