Bss1996
Introduction to Molecular Modelling 2
NH3 molecule
Calculation Method - RB3LYP
Basic set - 6-31G(d,p)
Final Energy E (au) - -56.497570525
Point Group - C3v
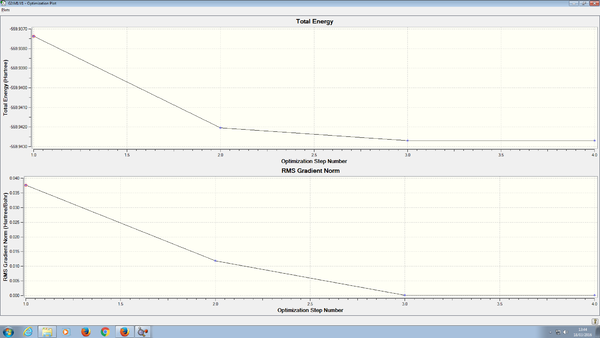
Item Value Threshold Converged? Maximum Force 0.101823 0.000450 NO RMS Force 0.068634 0.000300 NO Maximum Displacement 0.187375 0.001800 NO RMS Displacement 0.123109 0.001200 NO
NH3 Optimized |
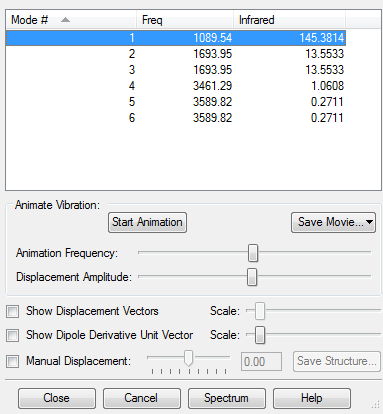
Vibrational Mode
Questions to answer
1) By 3N-6 rule, the expected number of modes is 6
2) The 1693.95 and 3589.82 (Freq) have degenerate energy
3) The 1089.54 and 3461.29 (Freq) are stretching while 1693.95 and 3589.82 (Freq) are bending modes
4) The 3461.29 (Freq) would be the highly symmetrical mode
5) The 1089.54 (Freq) would be the 'umbrella' mode
6) There would be 4 bands as there are 2 each of degenerate modes.
Charge Analysis
N-atom charge - (-1.125)
H-atom charge - (0.374)
N-atom has a negative charge while H-atom has a positive charge because N-atom is highly electronegative compared to H-atom thus N-atom would be negatively charged.
Haber-Bosch Process Reaction
N2 molecule and H2 molecule
Calculation Method - RB3LYP
Basic Set - 6-31G(d.p)
Point Group (Both) - D∞h symmetry
Vibrations (N2) - 2457.33 (Freq) / IR (0.000)
Vibrations (H2) - 4465.68 (Freq) / IR (0.000)
The Vibration modes of these compounds have no change in dipole moment during a stretching motion thus the IR value of them are 0 and they have no other modes because they are diatomic linear compounds.
(N=2 3N-5= 1)
Items of N2
Item Value Threshold Converged? Maximum Force 0.042835 0.000450 NO RMS Force 0.042835 0.000300 NO Maximum Displacement 0.011569 0.001800 NO RMS Displacement 0.016360 0.001200 NO
Items of H2
Item Value Threshold Converged? Maximum Force 0.168347 0.000450 NO RMS Force 0.168347 0.000300 NO Maximum Displacement 0.119698 0.001800 NO RMS Displacement 0.169278 0.001200 NO
N2 + 3 H2 → 2 NH3 (Haber Process) (Referenced Below)
E(N2) - -109.52412969 (au)
E(H2) - -1.15928020(au)
1) E(NH3)= -56.55776873
2) 2*E(NH3)= -113.11553746
3) E(N2)= -109.52412969
4) E(H2)= -1.15928020
5) 3*E(H2)= -3.4778406
6) ΔE= -0.11356717 (au) / -298.17 (kJ/mol)
The product of the process would be more stable as the forward process is a exothermic reaction thus the product has a lower energy; however, the value calculated from E gained from optimized structures of the molecules are different from the literature values. The literature value is -92.4kJ/mol which shows that there is a 223% percent error from the literature value. This shows values gained from the optimization is quite different from the literature values, which shows that the optimization performed had errors; however, it is also important to note that the overall ΔE is still the same sign so it is not as bad as it shows. The reasons of having big percentage error might be down to the small values that the calculations using a.u deals with. Thus also differences in the values in a.u can bring large errors as the the a.u is multiplied by a factor of 2625.5 to convert it into kJ/mol.
Molecule of Choice (Cl-F) Investigation
Information about Cl-F
Optimization of Cl-F
Calculation Method - RB3LYP
Basic Set - 6.31G(d.p)
Point Group - C*V
E(Cl-F) - -559.93737432 (a.u)
Charges on (Cl) and (F) atoms
(Cl) atom - (0.337)
(F) atom - (-0.337)
(F) atom is extremely electronegative compared to (Cl) atom so (F) atom has a negative charge.
Items of Cl-F
Item Value Threshold Converged?
Maximum Force 0.065262 0.000450 NO
RMS Force 0.065262 0.000300 NO
Maximum Displacement 0.056050 0.001800 NO
RMS Displacement 0.079267 0.001200 NO
Predicted change in Energy=-3.703919D-03
Cl-F Optimized |
Vibration Modes
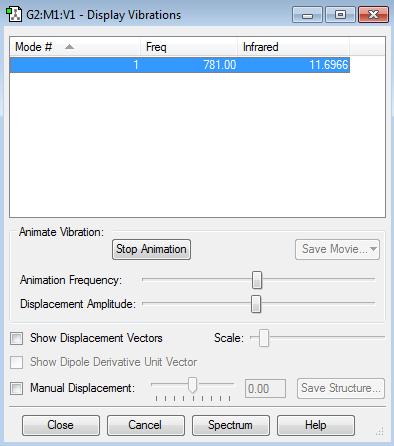
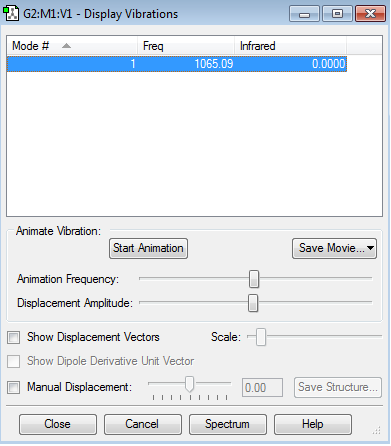
There is only 1 vibrational mode by 3N-5 rule (N=2)
There is only one mode, stretching, because the molecule is linear molecule with two atoms(N=2); however, it does have a dipole in the molecule as the two atoms have different electronegativity (Cl&F) thus it does have an IR value as the dipole moment changes when it absorbs it.
F2 and Cl2 molecule
Optimization Calculation Method - RB3LYP
Basic Set - 6-31G(d.p)
Point Group (Both) - D*H
E(F2) - -199.49825218 (a.u)
Items of F2
Item Value Threshold Converged? Maximum Force 0.402761 0.000450 NO RMS Force 0.402761 0.000300 NO Maximum Displacement 0.144433 0.001800 NO RMS Displacement 0.204259 0.001200 NO
E(Cl2) - -920.34987886 (a.u)
Items of Cl2
Item Value Threshold Converged? Maximum Force 0.024325 0.000450 NO RMS Force 0.024325 0.000300 NO Maximum Displacement 0.032742 0.001800 NO RMS Displacement 0.046304 0.001200 NO
Vibrational Modes of F2 and Cl2
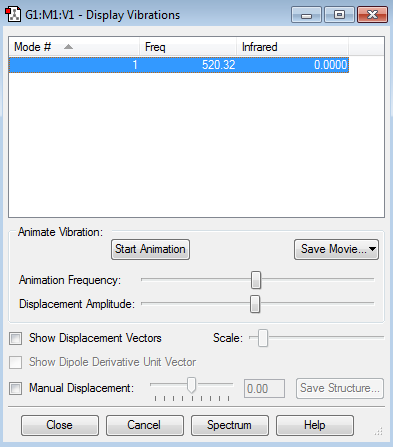
Cl2 Molecule Vibrational Mode (N=2 3N-5=1)
The Vibrational Mode is linear
The two molecules are diatomic linear molecules thus the dipole moment would not change by bending or stretching; therefore, have 0 IR value
F2 molecule Vibrational Mode (N=2 3N-5=1)
The Vibrational Mode is linear
File:CL2 LOL.log File:F2 LOL.log
Cl2 molecule optimized |
F2 molecule optimized |
Reactions and MOs
E(Cl-F) - -559.93737432 (a.u)
2E(Cl-F) - -1119.8747486(a.u)
E(F2) - -199.49825218 (a.u)
E(Cl2) - -920.34987886 (a.u)
ΔE= -0.02661758 (a.u) / -69.88 (kJ/mol)
The reaction is exothermic thus the product is more stable than the reactants.
MO Analysis
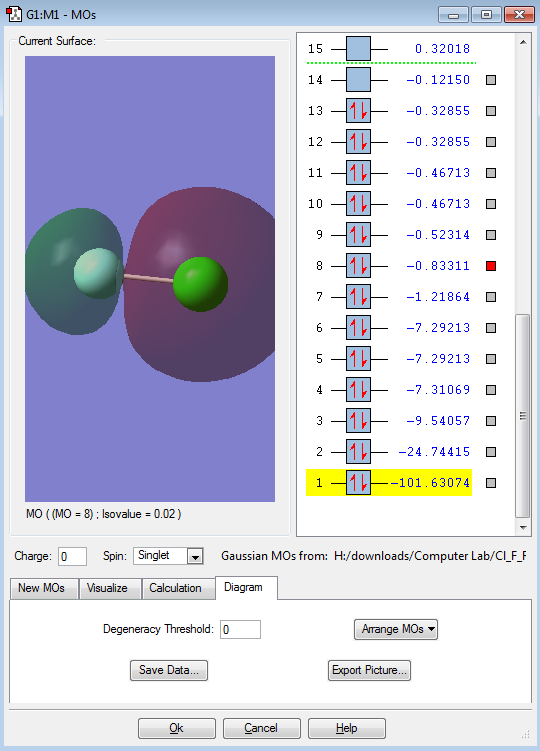
This is an bonding orbital formed from the linear in-phase linear interaction of the p-orbitals. This is the most stable p orbital bonding orbital due to linear nature of the interaction. This is the overall bond of the system as the anti-bonding orbital of this is LUMO so the anti-bond is not occupied.
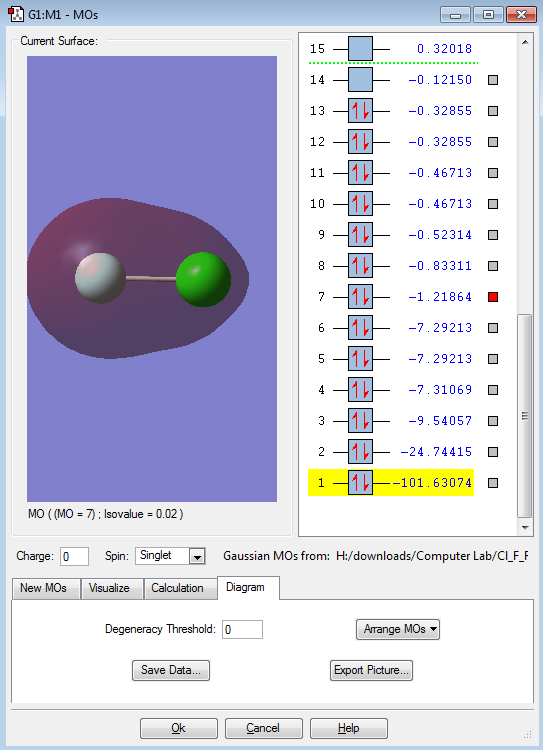
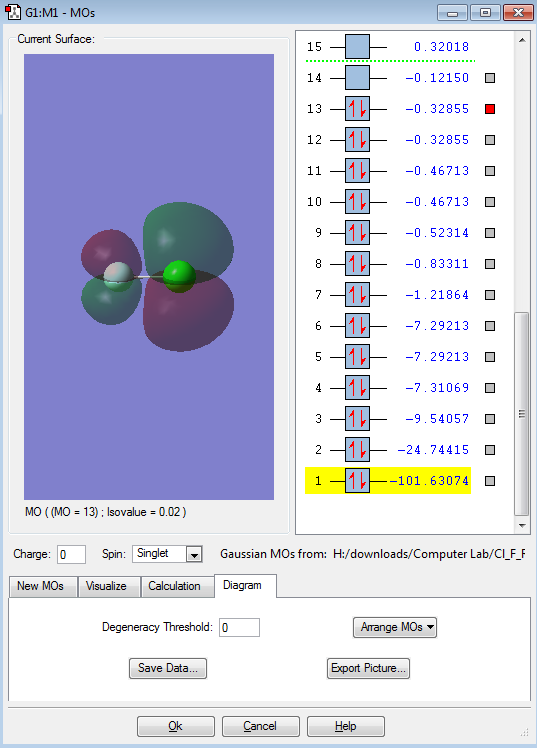
This is an bonding orbital formed from the in-phase interaction of the two 2s orbitals. It is interesting to see that the values on the right hand side (-1.21864) is much higher than that of it below, goes down to -101.63074. This shows that this MO has high energy and further away. Also, the asymmetrical shape shows the difference in the electronegativity.
This would be the anti-bonding orbital of the in-phase interaction of the two 2s orbitals ( MO above ) thus the interaction of the anti-bonding orbital would be an anti-phase interaction. It is interesting to note that the bonding and anti-bonding orbitals are in a sequence ( 7 & 8 ) which shows that the MOs above using p orbital to interact have a higher energy.
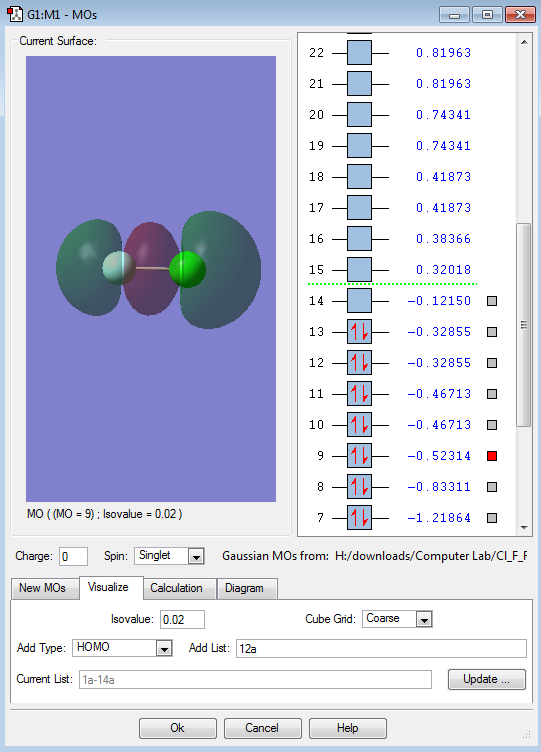
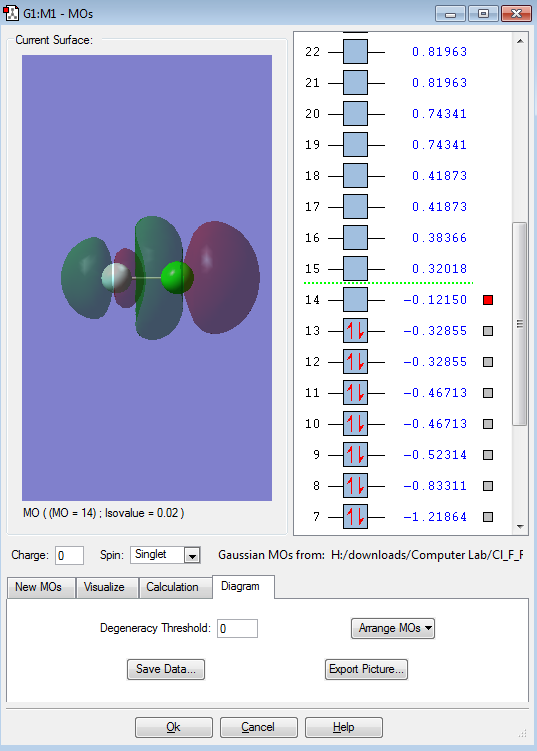
This is the LUMO ( Lowest Unoccupied Molecular Orbital ). It is a anti-bonding orbital formed from the anti-phase linear interaction of the two p orbitals. It shows the differences sizes of the of the AO of each atom (Cl and F). As this anti-bonding orbital is unoccupied so its bonding orbital is not broken ( First Image).
This is the HOMO ( Highest Occupied Molecular Orbital ). It is the anti-bonding orbital formed from the anti-phase parallel interaction of the two p orbitals. This orbital has the same energy (degenerate) to the MO 13 as that MO is also anti-phase parallel orbital but in a different direction compared to 12. Their (12 & 13) bonding orbital counterparts (10 & 11) have lower energy due to the difference of a anti-bonding and bonding orbital, and the bonding orbitals (10&11) also have degenerate energy as their interaction is identical (in-phase parallel).
References
Prof B. Shakhashiri, 'Ammonia', Chemical of the Week, General Chemistry, www.scifun.org, revised 2008