BrendanRogersComputational
Introduction to molecular modelling
TASK 1 NH3 Optimisation
Optimisation method: RB3LYT
Basis set: 6-31G
Final energy: -56.55776873 (au)
RMS Gradient: 0.00000494 (au)
Point group: C3V
N - H bond distance: 1.01798 au
N - H bond angle: 105.741 o
Item Value Threshold Converged?
Maximum Force 0.000280 0.000450 YES
RMS Force 0.000184 0.000300 YES
Maximum Displacement 0.000915 0.001800 YES
RMS Displacement 0.000434 0.001200 YES
Predicted change in Energy=-3.244629D-07
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.0176 -DE/DX = 0.0003 !
! R2 R(1,3) 1.0176 -DE/DX = 0.0003 !
! R3 R(1,4) 1.0176 -DE/DX = 0.0003 !
! A1 A(2,1,3) 105.7785 -DE/DX = 0.0 !
! A2 A(2,1,4) 105.7785 -DE/DX = 0.0 !
! A3 A(3,1,4) 105.7785 -DE/DX = 0.0 !
! D1 D(2,1,4,3) -111.93 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
Completed optimisation lab file: BR516_NH3_OPTF_POP.LOG
test molecule |
Task 2
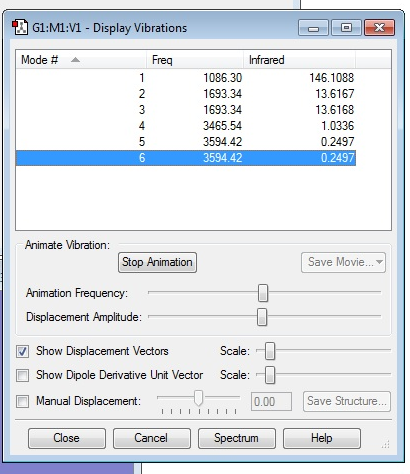
From the 3N-6 rule, you'd expect 6 modes of vibration as 3*4-6 = 6
Modes 2 and 3 are degenerate, and modes 5 and 6 are also degenerate. Modes 1, 2 and 3 are bends, whereas modes 4, 5 and 6 are stretches Mode 4 is highly Symmetric Mode 1 is the umbrella mode of vibration I would expect to see 4 bands in the gaseous spectrum of ammonia, as there are 4 different energy levels of vibration.
The Charge on the nitrogen atom is calculated at -1.125, and the charge on each hydrogen atom is calculated at +0.375 This makes sense, as the Nitrogen atom is highly electronegative and would pull electron density away from the hydrogen nuclei
Task 3
H2 Molecule data
Optimisation method: RB3LYT
Basis set: 6-31G
Final energy: -1.17835689 (au)
RMS Gradient: 0.00000017 (au)
Point group: D*H
H - H bond distance: 0.74279 au
Frequency of Vibration: 4465.68
Item Value Threshold Converged?
Maximum Force 0.000000 0.000450 YES
RMS Force 0.000000 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000001 0.001200 YES
Predicted change in Energy=-1.164079D-13
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 0.7428 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
Completed optimisation lab file: BR516_H2.LOG
test molecule |
N2 Molecule Data
Optimisation method: RB3LYT
Basis set: 6-31G
Final energy: -109.52412868 (au)
RMS Gradient: 0.00000365 (au)
Point group: D*H
N - N bond distance: 1.10550 au
Frequency of Vibration: 2457.31
Item Value Threshold Converged?
Maximum Force 0.000006 0.000450 YES
RMS Force 0.000006 0.000300 YES
Maximum Displacement 0.000002 0.001800 YES
RMS Displacement 0.000003 0.001200 YES
Predicted change in Energy=-1.248809D-11
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !<code></code>
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.1055 -DE/DX = 0.0 !
-------------------------------------------------------------------------------
Completed optimisation file: BR516_N2(2).LOG
test molecule |
Calculating energy differences in formation of NH3
E(NH3)= -56.55776873 au
2*E(NH3)= -113.11553746 au
E(N2)= -109.52412868 au
E(H2)= -1.17835689 au
3*E(H2)= -3.53507067 au
ΔE=2*E(NH3)-[E(N2)+3*E(H2)]= -113.1155374 - (-109.52412868 + -3.53507067) = -0.03805635 au = -99.916946925 Kj/mol
The negative change in internal energy shows that this is an exothermic reaction, so the ammonia product is more stable than the gaseous reactants. However, this result is considerably lower than the standard enthaply of formation of NH3, 1167 kJ/mol. This shows that while the calcualted theoretical value gives a good estimate of energy values, real values may differ wildly.
Task 4: Analysis of SiH4
Optimisation method: RB3LYT
Basis set: 6-31G
Final energy: -291.88802759(au)
RMS Gradient: 0.00001801 (au)
Point group: TD
Si - H bond distance: 1.48495 au
Si - H bond angle: 109.471 o
Charge on Si atom: +0.629
Charge on H atoms: -0.157
Item Value Threshold Converged?
Maximum Force 0.000035 0.000450 YES
RMS Force 0.000019 0.000300 YES
Maximum Displacement 0.000182 0.001800 YES
RMS Displacement 0.000097 0.001200 YES
Predicted change in Energy=-1.266278D-08
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.4849 -DE/DX = 0.0 !
! R2 R(1,3) 1.4849 -DE/DX = 0.0 !
! R3 R(1,4) 1.4849 -DE/DX = 0.0 !
! R4 R(1,5) 1.4849 -DE/DX = 0.0 !
! A1 A(2,1,3) 109.4712 -DE/DX = 0.0 !
! A2 A(2,1,4) 109.4712 -DE/DX = 0.0 !
! A3 A(2,1,5) 109.4712 -DE/DX = 0.0 !
! A4 A(3,1,4) 109.4712 -DE/DX = 0.0 !
! A5 A(3,1,5) 109.4712 -DE/DX = 0.0 !
! A6 A(4,1,5) 109.4712 -DE/DX = 0.0 !
! D1 D(2,1,4,3) -120.0 -DE/DX = 0.0 !
! D2 D(2,1,5,3) 120.0 -DE/DX = 0.0 !
! D3 D(2,1,5,4) -120.0 -DE/DX = 0.0 !
! D4 D(3,1,5,4) 120.0 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
test molecule |
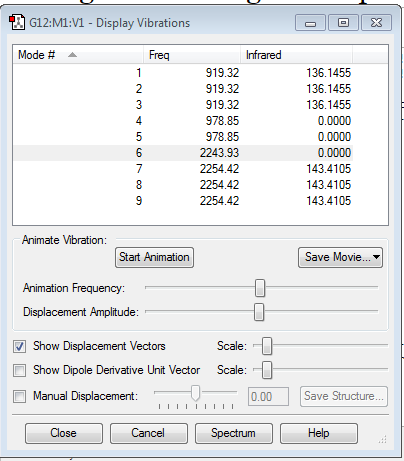
Vibration of SiH4
SH4 has 9 unique modes of vibration, in 4 degenerate energy levels. This agrees with the 3N - 6 rule, as SH4 has 5 atoms for 5*3 - 6 =9 modes of vibration.
Modes 1, 2 and 3 are degenerate, modes 4 and 5 are degenerate and modes 7, 8 and 9 are degenerate. Modes 6, 7, 8 and 9 are streches, while modes 1, 2, 3, 4 and 5 are bends.
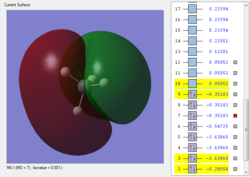
Molecular orbitals of SiH4
The lowest energy orbital is a non-bonding 1s orbital centered around the Si atom.

The second lowest energy orbital is another non-bonding 2s orbital centered around the Si atom.

The third lowest energy orbital set is a set of 3 degenerate orbitals, the 2p non-bonding orbitals around Si.

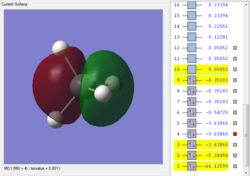
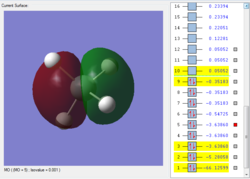
This is the first bonding orbital of the SiH4. It represents a combined orbital of the 4 sigma bonding orbital between the central Si atom and the surrounding 4 H atoms. This orbital was formed of a combination of a 3s orbital on the Si as well as the 1s orbitals on the hydrogens.
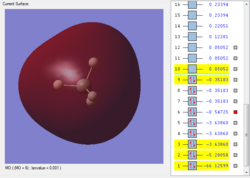
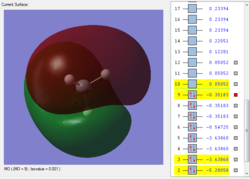
This is the second bonding orbital of SiH4, as there is minimal overlap between the combined molecular orbitals. It is formed of an Si 3p orbital, combined with the 4 1s orbitals on the hydrogens, execpt the 2 halves are out of phase with each other. The electron density is centered around the bonds to attract the hydrogens to the Si.