Bc608 module2
Normal 0 false false false EN-GB X-NONE X-NONE
Inorganic Computational Lab: Ben Chappell (CID:00513494)
Introduction
In this lab, ab initio ("from scratch") quantum mechanical calculations are utilised in order to gain an insight into the structure and bonding of Inorganic complexes. DFT calculations with the B3LYP functional are used exclusively throughout this lab, due to their wide applicability and extensive use in wider research.[1] The basis sets for the calculations are discussed in each section, with an initial discussion of basis sets provided in the examination of BH3.
Gaussian 09W is used to perform calculations, whilst GaussView v5.0 is used to create, edit and display files used and generated by Gaussian.
BH3
Geometry Optimisation
In the calculation methods discussed in this lab, atomic orbitals are modelled by Slater Type Orbitals (STO), which show a dependance upon 1/r. Molecules are held together by Molecular Orbitals, which result from the combination of atomic orbitals. Therefore, in order to model a molecule computationally, we must combine Slater Type Orbitals. Unfortunately, Slater Type Orbitals are computationally demanding to manipulate and combine. In order to get around this problem and to increase computational speed, each STO can be approximated by a number of Gaussian Type Orbitals (GTOs). Gaussians are dependant upon 1/r2 and thus by themselves do not accurately describe an atomic orbital. However, a combination of a number of Gaussians is capable of describing an atomic orbital accurately. Gaussians are much easier to manipulate computationally, as the combination of two Gaussians merely gives another Gaussian. These functions are illustrated in Figure 1.
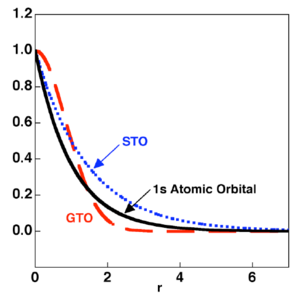
In order to make a computational description of a system more accurate, more STOs can be used to approximate each AO and more GTOs can be used to describe each STO. However, as the number of functions involved increases, so does the computational cost of the calculations. Therefore the number of functions used to describe a system must be carefully considered and a balance between computational cost and accuracy achieved.
When choosing a basis set, the first important factor to be considered is the number of STOs that will be used to approximate each AO. As more STOs are used to describe each AO, the accuracy of the calculations to reality is improved, but the computational cost is increased. Rather than increasing the number of STOs equally for all AOs in the system therefore, it makes more sense to be selective about which AOs are described more accurately. Most chemistry, reactivity and bonding occurs via valence orbitals, therefore a more accurate description of valence AOs will have more of an effect on accuracy than increasing the description of core AOs. Advanced basis sets, often utilise multiple STOs to describe each valence orbital, whereas core AOs are described by only one STO.
The 3-21G basis set used in the optimisation of BH3 is a minimal basis set, that is it uses the minimum number of STOs to describe each occupied AO of the system. Thus one STO is used to describe each occupied AO. In the case of BH3 this corresponds to the hydrogen 1s, the boron 1s, the boron 2s and the boron 2p atomic orbitals.
The next important factor is the number of GTOs that will be used to describe each STO. As before, increasing the number of GTOs increases the approximation of the STO, but also increases the computational cost. The 3-21G basis set is a "split valence" basis set, in which the method of STO approximation is different for core and valence orbitals.
For core orbitals, 3 GTOs are combined to describe each STO. The STO is approximated by a function of the form: f(x) = aGTO1 + bGTO2 + cGTO3, where a,b and c are weighting coefficients.
For valence orbitals, 3 GTOs are also used to describe each STO, but the 3 GTOs are contracted in a pattern of 2:1. This means, two of the GTOs share the same weighting coefficient. The STO is therefore approximated by a function of the form: f(x) = d (GTO1 + GTO2) + eGTO3, where d and e are weighing coefficients.
The justification for treating core orbitals more accurately is that the energy of these orbitals will dominate the total energy of the system and thus their accurate calculation is important.
One would expect the 3-21G basis set to therefore provide an ok approximation of the total energy of the system, but to reflect reactivity poorly, due to the contracted GTOs used in the approximation of the valence STOs. Contraction of valence GTOs is performed to increase computational speed.
Now the basis set has been understood, it is important to ask if it will accurately model BH3. The system to be modelled is very simple and highly symmetric, therefore it is likely that the simple description will be sufficient.
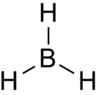
The structure of BH3 was optimised using DFT calculations using B3LYP functional and a 3-21G basis set. A Jmol of the optimised structure is shown to the right. The log file can be found here: DOI:10042/to-7581 The summary of the calculation is shown in Figure 2.
| BH3 Optimisation | |
| File type | .log |
| Calculation Type | FOPT |
| Calculation Method | RB3LYP |
| Basis Set | 3-21G |
| E(RB+HF-LYP) | -26.462 Hatrees +/- 3.808x10-3 |
| RMS Gradient Norm | 0.000 a.u. +/- 3.808x10-3 |
| Imaginary Frequencies | - |
| Dipole moment | 0.00 debye +/- 0.005 |
| Point group | D3H |
| Job time | 16.0 seconds |
Figure 2: A table to show the summary of the optimisation of BH3
The log file was checked in order to assume that the optimisation had converged. The relevant section in the log file is shown in Figure 3. It was seen that all parameters had converged. This is a necessary step in order to ensure the job has completed properly and has not failed.
Item Value Threshold Converged? Maximum Force 0.000090 0.000450 YES RMS Force 0.000059 0.000300 YES Maximum Displacement 0.000352 0.001800 YES RMS Displacement 0.000230 0.001200 YES Predicted change in Energy=-4.580970D-08 Optimization completed. -- Stationary point found.
Figure 3: The section of the output file which showed the calculation had converged
The optimisation procedure proceeded through 5 iterations, the structure of each iteration is shown in Figure 4.

In order to understand the optimisation procedure, it's imperative to first recall the Born Oppenheimer approximation.
The Born Oppenheimer approximation states that electrons move so very much faster than the relatively slow nuclei. The electrons can therefore change their positions instantaneously to respond to a change in nuclei position and therefore the momenta of nuclei does not affect the wavefunction of the electrons i.e. from the perspective of the electrons, the nuclei are stationary. It is important to note that the wavefunction of the electrons still depends upon the positions of the nuclei as there is a Coulombic attraction between the electrons and the nuclei. However, it does not depend upon the nuclei's momenta.
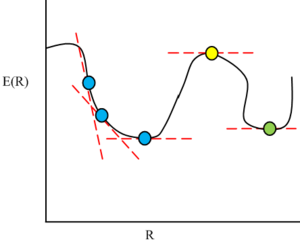
During the optimisation procedure, the energy of the system is calculated by solving the Schrodinger equation under the Born Oppenheimer approximation for a given set of nuclear positions. If all the nuclear positions are represented by R, then the energy calculated by solving the Schrodinger equation at these nuclear positions is E(R). The forces of the interactions between electrons and nuclei are then calculated at R. The nuclear positions are then altered i.e. R is changed to R'. The energy E(R') is then calculated and the forces calculated at R'. For every iteration, the absolute value of the rate of change of E(R) with R is calculated and this is the Root Mean Squared Gradient.
The 'optimised' structure is defined as the structure of lowest energy and is therefore a minima on the global potential energy surface. The process of reaching this minima from a starting point is termed "optimisation". As minima are a type of stationary point, the root mean squared gradient at the optimised structure is 0. The procedure of energy calculation, gradient calculation and nuclear position adjustment is repeated iteratively until a stationary point is reached.
The optimisation procedure is shown graphically in Figure 5.
The optimisation procedure for BH3 is shown in Figure 6.
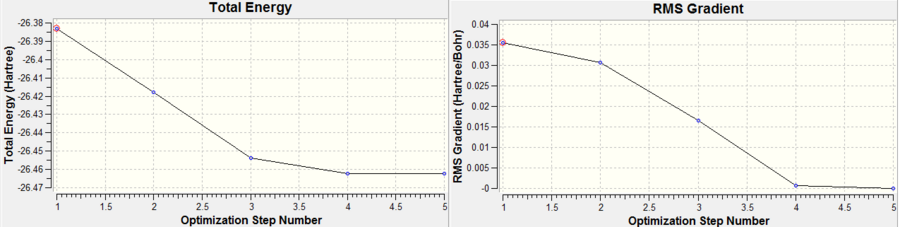
Whilst a stationary point has been found, it is not certain that the job has converged to a minimum and even if it has, if the right minimum has been converged to! In order to ensure this, analysis of the vibrational frequencies has to be performed.
If we are at a minima, then any movement of atoms and therefore electrons relative to others(e.g. a stretch of a bond) will result in a higher energy state and thus energy will have to be invested to make the movement happen. However, if we were at a maxima, a specific change in R will result in a decrease in E(R) i.e. energy is released when the movement happens.
This provides a means of distinguishing between convergence to a maxima or a minima. Minima will have entirely positive vibrational frequencies. Maxima will possess one negative vibrational frequency. If more than one negative vibrational frequency is present then a stationary point has not been found.
Vibrational analysis
Vibrational analysis to confirm a minima and comparison of measured parameters to literature
The vibrational frequencies of the optimised structure of BH3 were calculated using DFT-B3LYP and a 3-21G basis set.
It's important to note that the same calculation type and basis set is necessary. The 'optimised structure' is only a minima on the Potential Energy Surface calculated using DFT-B3LYP and a 3-21G basis set. The 'optimised structure' is not necessarily a minima on the PES calculated by other methods or other basis sets. If the calculation were performed using a different calculation type, method or basis set, then it is highly likely that one or more negative frequencies would result. This illustrates an important point: results obtained from calculations are accurate only to the level of theory and basis set used. Different methods and basis sets will give different results!
A summary of the frequency calculation is shown below in Figure 7. DOI:10042/to-7486
| Vibrational analysis of BH3 | |
| File type | .log |
| Calculation Type | FREQ |
| Calculation Method | RB3LYP |
| Basis Set | 3-21G |
| E(RB+HF-LYP) | -26.462 Hatree +/- 3.808x10-3 |
| RMS Gradient Norm | 0.000 Hatree +/- 3.808x10-3 |
| Imaginary Frequencies | 0 |
| Dipole moment | 0.00 debye +/- 0.005 |
| Point group | D3H |
| Job time | 17.4 seconds |
Figure 7: A table to show the summary of the calculation
The total energy of the system was found to be the same as the energy recorded for the optimisation. This confirmed the optimisation had been performed on the correct file.
The frequencies found to be result of translation of the whole molecule without bond distortion were found to be: 0, 0, 0, 37, 38 and 38 cm-1. These frequencies should be close to zero - the more accurate the method and basis set employed the closer to zero these values will be.
The lack of proximity to zero in this case can be attributed to the limited basis set utilised in this calculation, as discussed previously. However, the largest of these frequencies 38 cm-1 is still 2 orders of magnitude smaller than the lowest frequency vibration (1146 cm-1). For the purposes of this experiment, this will suffice. The results from the frequency analysis are shown in Figure 8.
| Stretching Mode # | Form of the vibration | Description | Frequency (error in frequency) /cm-1 | Intensity | Symmetry within the D3H point group |
| 1 |
|
The 3 hydrogens move together in the z direction, with the boron moving in the opposite direction at all times so that the Centre of Mass of the molecule does not change over the vibration | 1146 (± 115) | 93 | A2'' |
| 2 | One H-B-H angle is contracted, whilst the two other H-B-H angles are expanded. The two hydrogens moving down is counteracted by the remaining Boron and hydrogen moving upwards so that the centre of mass does not change over the vibration | 1205 (± 121) | 12 | E' | |
| 3 | One H-B-H angle is held constant, whilst another contracts and the third is expanded. The large movement of the hydrogen moving to change the two H-B-H angles is counteracted by smaller movements of the remaining atoms so that the Centre of Mass does not change over the vibration | 1205 (± 121) | 12 | E' | |
| 4 | All B-H bonds stretch symmetrically at the same time. The central Boron does not move throughout the vibration. The symmetry of the vibration means that the Centre of Mass does not change over the vibration. | 2592 (± 259) | 0 | A1' | |
| 5 | One B-H bond has a constant length, the remaining two lengthen and shorten asymmetrically. The hydrogen not involved in stretching and the Boron are moved to counteract the movements of hydrogens so that the centre of mass does not change over the vibration. | 2730 (± 273) | 104 | E' | |
| 6 | Two B-H bonds stretch symmetrically, whereas the third stretches asymmetrically with respect to the other two. When the two B-H bonds lengthen, the third will shorten and the Boron will travel upwards so that there is no change in the centre of mass over the vibration. | 2730 (± 273) | 104 | E' |
Figure 8: A table to show the summary of the calculation
In the vibrations, not only are the hydrogen atoms moving, but the important Although it is nice to have animations of the vibrations, the purpose of this part is to help you think about the atomic movements and this is achieved by you drawing out and describing the different motions, from an understanding point of view just making a movie of the vibration doesn't do this, so a maximum of ONE animation please! (lots of animations also cloggs up your wiki and makes it slow)
The lack of any negative stretching frequencies shows the optimised structure is in fact an energy minimum, but does not show that it is the global minimum. In order to be certain the structure has been correctly optimised, a comparison must be made to experimental data. In this case, a comparison of bond lengths and angles is possible.
The B-H bond distance was measured to be 1.19 Å ± 0.005 and the H-B-H angle measured to be 120° ± 0.05. Reported values for B-H bond lengths in a similar structure, BH4-, are of the order of 1.21 Å [3]. Thus the measured bond length does not seem unrealistic and it is likely that the structure has been optimised successfully.
Most importantly, the optimised structure makes chemical sense - one would expect BH3 to adopt a trigonal planar structure.
Vibrational analysis to calculate the IR spectrum of BH3
The results of the Vibrational Analysis are shown in Figure 8. Symmetry of each vibration was determined using a representation table. This process is illustrated in Figure 9 for the first vibration of A2'' symmetry. Each symmetry operation of the point group is performed upon the vibration. If the vibration remains unchanged under a symmetry operation, the element of the vibration under that symmetry operation is 1. If the vibration is reversed, the element of the vibration under that symmetry operation is -1.
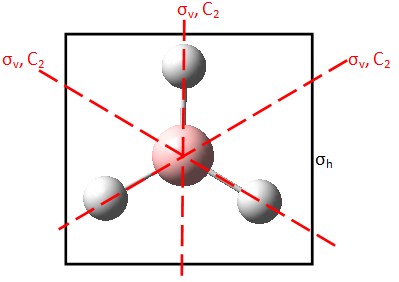 |
 |
| D3h | E | 2C3 | 3C2 | σh | 2S3 | 3σv |
Γ  |
1 | 1 | -1 | -1 | -1 | 1 |
Figure 9 : The representation table for the A2'' stretch
This procedure was performed for all the above vibrations. The IR spectrum was also calculated and is shown in Figure 10.
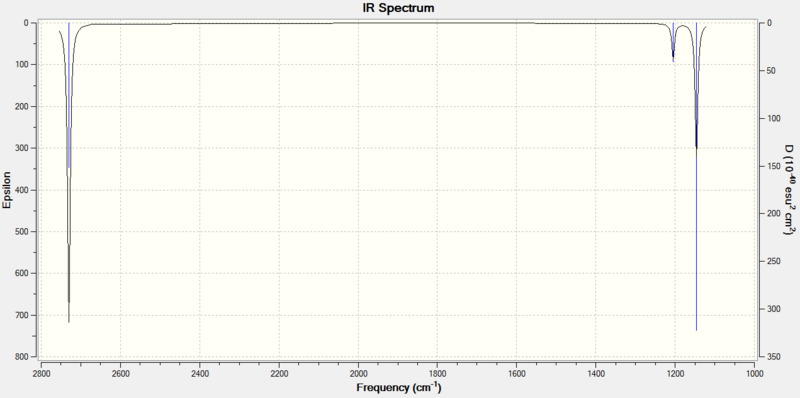
It can be seen that there are only 3 peaks observed in the IR spectrum of BH3, however we have calculated 6 vibrations!
In order to see a peak in an IR spectrum, light must be absorbed in the IR frequency range. In order for an absorption to occur, there must be a non-zero transition dipole moment. The dependency of transition dipole moment upon change in molecular dipole over the vibration is shown in the following equation:
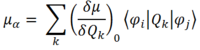
Where: μα is the transition dipole moment
(δμ/δQk)0 is the change in molecular dipole moment over the vibrational mode in question Qk
φi is the vibrational wavefunction at equilibrium
φj is the vibrational wavefunction at vibrational displacement j
It can therefore be seen that vibrational modes that do not give a change in molecular dipole moment over the vibration will have transition dipole moments equal to zero and therefore these vibrational modes are not IR active.
For mode #4, there is no change in dipole moment over the vibration because the stretching is totally symmetric, one would therefore expect this band to be IR inactive. This leaves 5 vibrational modes that display a change in dipole moment over the vibration.
It is now important to realise that vibrations #2 and #3 are degenerate. They are of the same energy and so occur at the same frequency - this is denoted by their e' label. The peak at 1205 cm-1 is the result of not one, but two vibrations of the same frequency. Vibrations #5 and #6 are also degenerate and both occur at 2730 cm-1. The third band occurs at 2592 cm-1 and is singly degenerate. Thus 3 peaks are observed in the IR spectrum, corresponding to 5 vibrations: 2 IR active degenerate pairs of vibrations and a 5th IR active vibration. The 6th vibration is totally symmetric and IR inactive.
Population Analysis: Molecular Orbitals of BH3, a comparison of qualitative and quantitative molecular orbital methods
The energy of the optimised structure of BH3 was calculated using DFT-B3LYP, a 3-21G basis set and full NBO and population analysis. DOI:10042/to-7487
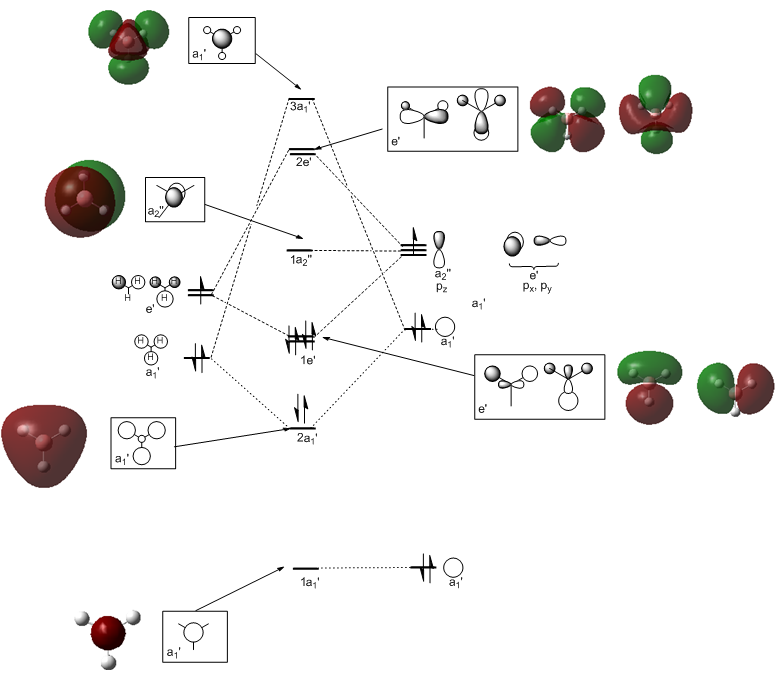
Qualitative Molecular Orbital Diagrams
A qualitative molecular orbital diagram was generated and can be seen in Figure 12. The fragment orbitals of H3 are constructed using a representation table (as in Figure 9), the reduction formula and the projection formula. Hydrogen and Boron are of similar electropositivity and thus of similar energy. The fragment orbitals of H3 all display bonding character, thus the a1' has been placed below the 1s orbital of Boron to reflect it being of lower energy. The e' levels of H3 have been estimated to be of comparable energy to the boron p orbitals. The orbitals are then mixed according to their symmetry labels. Only orbitals of the same symmetry can interact and each orbital only interacts once. Secondary orbital mixing occurs between molecular orbitals of the same symmetry, but it was judged to be insignificant in the case of BH3 as there are no orbitals of the same symmetry that are close in energy.
The relative ordering of the 3a' and the 2e' molecular orbitals is hard to evaluate qualitatively. The relative energies of molecular orbitals are given by the Klopman-Salem equation, which can be expressed in the following simplified form:
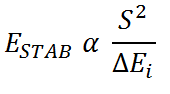
S2 is the overlap integral ESTAB is the stabilisation energy ΔEi is the interaction energy or the energy difference between interacting orbitals
By examining how the S2 and ΔEi of the Klopman-Salem equation vary for each overlap of fragment orbital, one determines the stabilisation/destabilisation of the resulting molecular orbitals relative to the initial fragment orbitals. By combining the stabilisation energy and the unperturbed fragment orbital energy, one can estimate the energy of a molecular orbital.
This analysis is fine for the majority of the orbitals of BH3, however a problem arises when considering the ordering of the 3a1' and 2e' MOs. Applying the above analysis:
Overlap: S orbitals overlap more effectively with other s orbitals than they do with p orbitals, so one would expect a larger S2 term for the 3a' molecular orbital than for the 2e' molecular orbital.
Interaction Energy: This is very hard to judge.
Fragment orbital energies: The a1' orbital on H3 is lower in energy than the e' orbitals. The 2s orbital of the Boron atom is lower in energy than the 2px and 2py orbitals. Thus the unperturbed fragment orbital energy is lower for the 3a1' MO than for the 2e' MO.
There are two opposite acting effects and a third that cannot be determined. Qualitative treatment gives us no indication which effect is larger. In order to determine the ordering of energy levels a quantitative treatment is required.
Quantitative Molecular Orbital Diagrams
The MOs from the population analysis were visualised. It can be seen from Figure 11 that the 3a' MO is in fact higher in energy than the 2e' MO at this level of theory. As previously mentioned, results can change dependent upon the basis set and calculation type used.
| Orbital | Orbital Energies ± 3.808x10-3 /Hatree |
| 1a1' | -6.726 |
| 2a'1 | -0.520 |
| 1e' | -0.358 |
| 1a2 | -0.074 |
| 2e' | 0.192 |
| 3a'1 | 0.199 |
Figure 11: A table to show the relative orbital energies of the BH3 molecular orbitals
On the whole, the calculated molecular orbitals are in excellent agreement with the qualitative LCAO molecular orbitals. The agreement between molecular orbitals is less good for unfilled molecular orbitals however, as can be seen by the right hand 2e' orbital (or perhaps this is just difficult to visualise.) In the mini project, most of the orbitals above the LUMO were very difficult to discern at least, so this statement is qualified by observations there if not here.
Qualitative molecular orbital theory is useful and accurate to an extent. It provides a quick means of understanding reactivity of compounds, for instance Natural Bond Orbitals can be used qualitatively to understand relatively complex processes, such as the Eschenmoser fragmentation.[4]
Whilst the ordering of energy of the 2e' and 3a1' molecular orbitals is difficult to determine qualitatively, in order to understand the reactivity of BH3 it doesn't much matter which orbital is lower in energy. The energy levels of the HOMO and LUMO are unambiguous in this case and it is these orbitals that will dominate reactivity. Computational MO theory is more useful for complex systems, where deriving the molecular orbitals "by hand" is more difficult.
Natural Bond Orbital Analysis of BH3: Charge distribution
NBO analysis on the optimised structure of BH3 was performed in an earlier calculation. DOI:10042/to-7487
NBO analysis takes a delocalised MO picture and returns a 2 electron-2 centre picture of bonding.
The log file was opened and the summary of Natural Population Analysis found. The summary shows the natural atomic charges and the population of core orbitals, valence orbitals and Rydberg orbitals (i.e. very diffuse orbitals that have principal quantum numbers higher than the atoms' valence orbitals). For instance the 1.99902 in the Core column of Boron represents the two electrons that are in the 1s atomic orbital of the Boron atom. This is shown in Figure 13.
Natural Population
Natural -----------------------------------------------
Atom No Charge Core Valence Rydberg Total
-----------------------------------------------------------------------
B 1 0.33679 1.99902 2.66419 0.00000 4.66321
H 2 -0.11226 0.00000 1.11193 0.00033 1.11226
H 3 -0.11226 0.00000 1.11193 0.00033 1.11226
H 4 -0.11226 0.00000 1.11193 0.00033 1.11226
=======================================================================
* Total * 0.00000 1.99902 6.00000 0.00099 8.00000
Figure 13: The summary of Natural Population Analysis
Gaussview can interpret the natural charges to give a more visual picture of the natural charges in the molecule. These are shown in Figure 14.
 |
 |
Figure 14: The charge distribution in BH3 as calculated by NBO analysis. Red denotes negative charge whereas green denotes positive charge. Numbers represent the NBO charges of the atoms.
The Boron is BH3 is shown to be highly electron deficient, as would be expected based upon the Lewis structure of the compound.
Examining the log file further, one can determine the bonding in the compound in terms of hybridisation.
(Occupancy) Bond orbital/ Coefficients/ Hybrids
---------------------------------------------------------------------------------
1. (1.99884) BD ( 1) B 1 - H 2
( 44.40%) 0.6663* B 1 s( 33.33%)p 2.00( 66.67%)
0.0000 0.5774 0.0000 0.0000 0.0000
0.8165 0.0000 0.0000 0.0000
( 55.60%) 0.7457* H 2 s(100.00%)
1.0000 0.0000
2. (1.99884) BD ( 1) B 1 - H 3
( 44.40%) 0.6663* B 1 s( 33.33%)p 2.00( 66.67%)
0.0000 0.5774 0.0000 0.7071 0.0000
-0.4082 0.0000 0.0000 0.0000
( 55.60%) 0.7457* H 3 s(100.00%)
1.0000 0.0000
3. (1.99884) BD ( 1) B 1 - H 4
( 44.40%) 0.6663* B 1 s( 33.33%)p 2.00( 66.67%)
0.0000 0.5774 0.0000 -0.7071 0.0000
-0.4082 0.0000 0.0000 0.0000
( 55.60%) 0.7457* H 4 s(100.00%)
1.0000 0.0000
4. (1.99902) CR ( 1) B 1 s(100.00%)
1.0000 0.0000 0.0000 0.0000 0.0000
0.0000 0.0000 0.0000 0.0000
5. (0.00000) LP*( 1) B 1 s(100.00%)
6. (0.00000) RY*( 1) B 1 s( 0.00%)p 1.00(100.00%)
7. (0.00000) RY*( 2) B 1 s( 0.00%)p 1.00(100.00%)
8. (0.00000) RY*( 3) B 1 s( 0.00%)p 1.00(100.00%)
9. (0.00000) RY*( 4) B 1 s( 0.00%)p 1.00(100.00%
Figure 15: The NBOs in BH3
The first three Natural Bond orbitals are between the Boron and a Hydrogen, 44.40% of each bond is contributed to by Boron orbitals that are sp2 hybridised (33.33% s character, 66.67% p character). 55.60% of each bond is contributed to by Hydrogen orbitals that are exclusively s character - as one would expect.
The 4th Natural Bond orbital is a core orbital centred on Boron, which is 100% s character. This will be the occupied 1s orbital of Boron, which does not participate in bonding.
The 5th Natural Bond orbital is interesting. One would expect the 5th orbital to be an unhybridised empty p orbital of boron, however the logfile has reported an empty orbital of 100% s character. The electronic structure of Boron is 1s22s22p2. The third p orbital of Boron must have been included in the minimal basis as one cannot determine which two of the three p orbitals the 2 p electrons reside in, therefore it is not entirely clear where it has gone.
The example in the lab instructions does indeed give the 5th NBO as an empty boron p orbital as expected. However, it is important to note that many of the example calculations were performed with a 6-31G basis set. It is therefore likely that the aphysical result seen using a 3-21G basis set is due to a limitation of applying this basis set to this calculation. It must be stressed that the limitation is not the result of a lack of inclusion of this third p orbital in the basis set, as it must have been included to describe a Boron atom. By examining the log file further, the empty Boron p orbital seems to being treated as a Rydberg orbital in higher NBOs. The cause of this is unknown.
The "Second Order Perturbation Theory Analysis of Fock Matrix in NBO Basis" section outlines mixing of MOs, however it does not show much information for BH3 as no significant second order mixing takes place.
Second Order Perturbation Theory Analysis of Fock Matrix in NBO Basis
Threshold for printing: 0.50 kcal/mol
E(2) E(j)-E(i) F(i,j)
Donor NBO (i) Acceptor NBO (j) kcal/mol a.u. a.u.
===================================================================================================
within unit 1
4. CR ( 1) B 1 / 10. RY*( 1) H 2 1.54 7.54 0.096
4. CR ( 1) B 1 / 11. RY*( 1) H 3 1.54 7.54 0.096
4. CR ( 1) B 1 / 12. RY*( 1) H 4 1.54 7.54 0.096
Figure 16: Molecular orbital mixing in BH3
Only values in the E(2) column greater than 20kcal/mol are deemed to be significant. It would seem there is an insignificant interaction here between the Boron 1s orbital and the Hydrogen's empty Rydberg orbitals, which is stabilising the Boron 1s orbitals slightly.
The last section gives a summary of the occupancy of the NBOs of BH3.
Natural Bond Orbitals (Summary):
Principal Delocalizations
NBO Occupancy Energy (geminal,vicinal,remote)
====================================================================================
Molecular unit 1 (H3B)
1. BD ( 1) B 1 - H 2 1.99884 -0.43956
2. BD ( 1) B 1 - H 3 1.99884 -0.43956
3. BD ( 1) B 1 - H 4 1.99884 -0.43956
4. CR ( 1) B 1 1.99902 -6.63856 10(v),11(v),12(v)
5. LP*( 1) B 1 0.00000 0.67133
6. RY*( 1) B 1 0.00000 0.37047
7. RY*( 2) B 1 0.00000 0.37047
8. RY*( 3) B 1 0.00000 -0.04349
9. RY*( 4) B 1 0.00000 0.43436
10. RY*( 1) H 2 0.00033 0.89768
11. RY*( 1) H 3 0.00033 0.89768
12. RY*( 1) H 4 0.00033 0.89768
13. BD*( 1) B 1 - H 2 0.00116 0.42928
14. BD*( 1) B 1 - H 3 0.00116 0.42928
15. BD*( 1) B 1 - H 4 0.00116 0.42928
-------------------------------
Total Lewis 7.99554 ( 99.9442%)
Valence non-Lewis 0.00348 ( 0.0435%)
Rydberg non-Lewis 0.00099 ( 0.0123%)
-------------------------------
Total unit 1 8.00000 (100.0000%)
Charge unit 1 0.00000
Figure 16: A summary of the NBO analysis in BH3
It can be seen that there are 2 electrons in each of the B-H bonds, 2 electrons in the Boron 1s and an empty orbital on Boron which is being treated as s character, but we know to be p character.
TlBr3
Pseudo potentials
TlBr3 is a compound that has 151 electrons. At the level of quantum mechanics being utilised in these calculations, computing the wavefunction for each of these orbitals would be computationally very expensive. Furthermore, the size of the atoms causes them to exhibit relativistic effects, which are not recovered easily by using the standard Schrodinger equation. In order to get around this problem, a pseudo potential is used. A pseudo potential is a potential used to model the core orbitals of an atom. This approximation is justified by the knowledge that core orbitals of atoms are not heavily involved in chemical bonding, which in the large part can be attributed to valence orbitals.
Furthermore, as a group is descended, valence orbitals become more diffuse and polarizable. Both of the atoms in this calculation are beyond the first row of the periodic table and thus these effects will be significant. The 3-21G basis set previously used therefore needs to be improved upon because the system is much more complex than was previously the case.
A LANL2DZ basis set is used to optimise TlBr3. This basis set uses the Los Alamos Effective Core Potential for core orbitals and double zeta basis functions for the valence atomic orbitals. "Double zeta basis functions" means that 2 Slater Type Orbitals are used to model each atomic orbital, which gives an improved description of the valence orbitals. This approach of improved description of the valence orbitals with multiple STOs, with a less accurate description of core orbitals was discussed in the Optimisation of BH3 section of this report.
Optimisation
The structure of TlBr3 was optimised using DFT-B3LYP and a LANL2DZ basis set. The optimised structure was constrained to be in the D3h point group to avoid false minima. The optimised structure is shown to the right. The logfile for the optimisation can be found here. https://wiki.ch.ic.ac.uk/wiki/images/4/4a/Bc608_TLBR3_GEO_OPT.LOG
A summary of the calculation is shown in Figure 17
| Optimisation of TlBr3 | |
| File type | .log |
| Calculation Type | FOPT |
| Calculation Method | RB3LYP |
| Basis Set | LANL2DZ |
| E(RB+HF-LYP) | -91.218 Hatree +/- 3.808x10-3 |
| RMS Gradient Norm | 0.000 Hatree +/- 3.808x10-3 |
| Imaginary Frequencies | 0 |
| Dipole moment | 0.00 debye +/- 0.005 |
| Point group | D3H |
| Job time | 26.0 seconds |
Figure 17: A table to show the summary of the calculation
Frequency Analysis to confirm a minimum and comparison of parameters to literature values
As for BH3, a confirmation that a minimum has been reached is needed. Frequency analysis was performed on the optimised structure of TlBr3 using DFT-B3LYP and a LANL2DZ basis set. A summary of the calculation is shown in Figure 18. The log file of the calculation can be found here. https://wiki.ch.ic.ac.uk/wiki/images/b/b5/BC608_TLBR3_FREQ.LOG A discussion of why the same method and basis set must be used was provided in the optimisation of BH3 earlier in this report.
| Frequency Analysis of TlBr3 | |
| File type | .log |
| Calculation Type | FREQ |
| Calculation Method | RB3LYP |
| Basis Set | LANL2DZ |
| E(RB+HF-LYP) | -91.218 Hatree +/- 3.808x10-3 |
| RMS Gradient Norm | 0.000 Hatree +/- 3.808x10-3 |
| Imaginary Frequencies | 0 |
| Dipole moment | 0.00 debye +/- 0.005 |
| Point group | D3H |
| Job time | 22.0 seconds |
Figure 17: A table to show the summary of the calculation
The low frequencies of TlBr3 were found to be -3, 0, 0, 0 and 4 cm-1.
The lowest 'real' mode of TlBr3 was found to be 46cm-1. The lowest low frequency was found to be an order of magnitude smaller than the lowest 'real' frequency and so the level of accuracy of the calculation is acceptable. The vibrational frequencies of TlBr3 are shown in Figure 18.
| Stretching Mode # | Frequency (error in frequency) /cm-1 | Intensity |
| 1 | 46 (± 5) | 4 |
| 2 | 46 (± 5) | 4 |
| 3 | 52 (± 5) | 6 |
| 4 | 165 (± 17) | 0 |
| 5 | 211 (± 21) | 25 |
| 6 | 211 (± 21) | 25 |
Figure 18: A table to show the frequencies of the vibrations of TlBr3
All the vibrations of TlBr3 were found to be positive. The absence of negative frequencies shows that a minimum has been reached.
Now a comparison to literature is required to check that the optimised structure is reasonable. The Tl-Br bond length in TlBr3 was measured to be 2.65Å ± 0.005 and the Br-Tl-Br bond angle measured to be 120.0° ± 0.05. The length of the Tl-Br bond was measured to be 2.512Å experimentally[5], so this value does not seem unrealistic. The bond angle of 120° makes intuitive sense. The structure of TlBr3 has therefore been successfully optimised using pseudo potentials.
What is a bond?
In some structures, Gaussview does not draw in bonds where we expect them to be. This is seen for the Molybdenum complex discussed after this section, where the P-Cl bonds are not drawn in. It is important to remember that Gaussview is merely a graphical interface that is used to set up calculations and view output files that Gaussian performs and creates. When interpreting output files to provide a visual image, Gaussview uses the proximity of atoms to decide the bond order between atoms. When Gaussview fails to display a bond, it is because Gaussview decides by comparison to standard bond lengths, the atoms are far apart for a bond to exist. Gaussview does not make any attempt to consider electron density between atoms when deciding whether a bond is present.
This is obviously a major limitation of Gaussview. A bond is a region of high electron density between two or more atoms that results in attractive forces between the nuclei involved. A bond between atoms cannot exist without shared electron density between the atoms. Thus it is clear that a mere distance relationship between nuclei is insufficient to describe a "bond" and electron density between involved atoms must be considered.
Gaussview may not draw the bonds in, but they are still there.
Cis and trans isomerisation of Mo(CO)4L2
In the second year synthesis lab, cis- and trans-Mo(CO)4PPh3 was prepared. 4 carbonyl absorption bands were observed from the cis complex, whereas only one band was observed from the trans complex.
In order to understand this observation, it would be desirable to compute the vibrations of the molecule. Unfortunately, performing calculations on the complexes directly will be too computationally expensive due to the bulky triphenylphosphines. However, a model system can be utilised, where computationally less demanding Cl atoms replace the phenyl groups. Chlorines could be expected to have similar electronic contributions to bonding as phenyl groups and like phenyl groups they are also sterically large. The cis and trans isomers of Mo(CO)4PCl3 were optimised with a successive optimisation procedure outlined below.
Initial loose optimisation
In the exercise, it was stated that Dr Hunt had searched over the rotational profile in order to find a good starting point for the optimisation. It is important to be selective with the starting point of the calculation in order to avoid false minima. As previously discussed in Figure 3, false minima are defined as local minima that are not the overall most stable structure of the molecule. Calculations may converge to these local minima as shown in Figure 19.
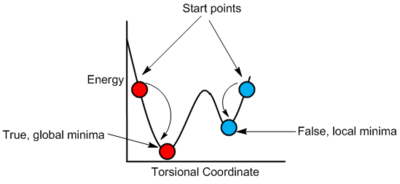
The starting geometries for the optimisations are shown in Figure 20.
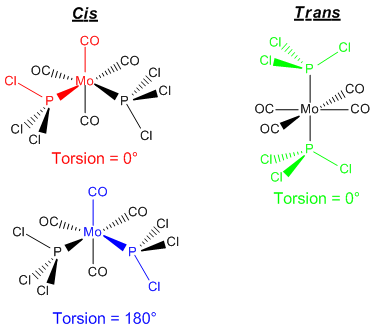
From these starting geometries, the DFT-B3LYP method was utilised using a LANL2MB basis set and loose optimisation conditions in order to get a rough optimisation so that the subsequent calculation would be more rapid. LANL2MB utilises a pseudo potential for core orbitals, whilst a minimal basis (1 STO for each AO) is used for the valence orbitals. Considering the complexity of the structure, this is not sufficient to model the structure, but it is a good starting point to get the geometry "roughly correct" for subsequent optimisations.
The calculation summary is shown in Figure 21.
| Loose Optimisation of Mo complex | ||
| Cis | Trans | |
| D-Space | DOI:10042/to-7495 | DOI:10042/to-7496 |
| File type | .log | .log |
| Calculation Type | FOPT | FOPT |
| Calculation Method | RB3LYP | RB3LYP |
| Basis Set | LANL2MB | LANL2MB |
| E(RB+HF-LYP) | -617.525 Hatrees ± 3.808x10-3 | -617.522 ± 3.808x10-3 |
| RMS Gradient Norm | 0.000 Hatrees ± 3.808x10-3 | 0.000 ± 3.808x10-3 |
| Dipole moment | 8.62 debye ± 0.005 | 0.31 ± 0.005 |
| Point group | C2 | CS |
| Job time | 8 minutes 7.0 seconds | 5 minutes 46.1 seconds |
Figure 21: A table to show the summary of the loose optimisation calculation
Double zeta basis set and pseudo potential optimisation
Using the roughly optimised output from the previous calculation, the geometry was more accurately optimised using the DFT-B3LYP method, a LANL2DZ basis set and ultrafine electronic convergence. As previously discussed, LANL2DZ is a double zeta basis set and uses two Slater Type Orbitals to model each valence atomic orbital. This will give a much better description of the valence atomic orbitals and should describe the bonding in the complex much more accurately.
The job was performed, checked and found to converge. The calculation summary is shown in Figure 22.
| Double zeta basis set and pseudo potential optimisation | ||
| Cis | Trans | |
| D-Space | DOI:10042/to-7499 | DOI:10042/to-7498 |
| File type | .log | .log |
| Calculation Type | FOPT | FOPT |
| Calculation Method | RB3LYP | RB3LYP |
| Basis Set | LANL2DZ | LANL2DZ |
| E(RB+HF-LYP) | -623.577 Hatree ± 3.808x10-3 | -623.576 Hatree ± 3.808x10-3 |
| RMS Gradient Norm | 0.000 Hatree ± 3.808x10-3 | 0.000 Hatree ± 3.808x10-3 |
| Dipole moment | 1.3072 debye ± 0.005 | 0.3039 ± 0.005 |
| Point group | C2 | CS |
| Job time | 22 minutes 57.8 seconds | 19 minutes 46.0 seconds |
Figure 22: A table to show the summary of the second optimisation
It is important to note that this calculation implies that the cis complex is more stable than the trans comples by 2.6 KJ mol-1. However, it's important to realise that this difference is small and within the error of the calculation, which is approximately 10 KJ mol-1 One major failing of this calculation is the lack of treatment of phosphorous d orbitals. Phosphorous often displays hypervalency and can utilise low lying d orbitals in order to accomplish this. This complex may show some Phosphorous d character in its bonding and so the phosphorous d orbitals in this compelex cannot be reasonably ignored.
Including Phosphorous d orbitals
Phosphorous d orbitals were accounted for by including an extra basis, the following was added to the bottom of the input file.
| (blank line) |
| P 0 |
| D 1 1.0 |
| 0.55 0.100D+01 |
| **** |
| (blank line) |
This essentially includes 5 extra atomic orbitals to be calculated corresponding to the unfilled d orbitals on phosphorous. In order to model the 5 new AOs, 10 extra STOs are required (2 for each AO as it is a double zeta basis set), which results in a computationally more demanding calculation.
The cis and trans structures were then reoptimised using DFT-B3LYP, ultrafine electronic convergence and the new adapted basis set. The summaries of the calculations are shown in Figure 23.
| Double zeta basis set and pseudo potential optimisation | ||
| Cis | Trans | |
| D-Space | DOI:10042/to-7501 | DOI:10042/to-7500 |
| File type | .log | .log |
| Calculation Type | FOPT | FOPT |
| Calculation Method | RB3LYP | RB3LYP |
| Basis Set | LANL2DZ with added d orbitals for phosphorous | LANL2DZ with added d orbitals for phosphorous |
| E(RB+HF-LYP) | -623.693 Hatree ± 3.808x10-3 | -623.694 Hatree ± 3.808x10-3 |
| RMS Gradient Norm | 0.000 Hatrees ± 3.808x10-3 | 0.000 Hatree ± 3.808x10-3 |
| Dipole moment | 0.0731 debye ± 0.005 | 0.2293 ± 0.005 |
| Point group | C2 | CS |
| Job time | 19 minutes 3.2 seconds | 21 minutes 24.7 seconds |
Figure 23: A table to show the summary of the third optimisation
The output files were checked and both jobs found to converge.
Frequency Analysis to confirm the Minima
Frequency analysis was performed in order to ensure both isomers were at a minimum. The summary of the calculation is shown in Figure 24.
| Double zeta basis set and pseudo potential frequency optimisation | ||
| Cis | Trans | |
| D-Space | DOI:10042/to-7523 | DOI:10042/to-7524 |
| File type | .log | .log |
| Calculation Type | FREQ | FREQ |
| Calculation Method | RB3LYP | RB3LYP |
| Basis Set | LANL2DZ with added d orbitals for phosphorous | LANL2DZ with added d orbitals for phosphorous |
| E(RB+HF-LYP) | -623.693 Hatree ± 3.808x10-3 | -623.694 Hatree ± 3.808x10-3 |
| RMS Gradient Norm | 0.000 Hatree ± 3.808x10-3 | 0.000 Hatree ± 3.808x10-3 |
| Imaginary Freq | 0 | 0 |
| Dipole moment | 0.0731 debye ± 0.005 | 0.2293 ± 0.005 |
| Point group | C2 | CS |
| Job time | 21 minutes 39.0 seconds | 22 minutes 47.5 seconds |
Figure 24: A table to show the summary of the calculation
No negative frequencies were seen, confirming the minima. Note: The vibrational modes themselves are discussed in a subsequent section.
In order to check that a reasonable structure had been reached, the bond lengths and angles for the trans isomer were measured and compared to Mo(CO)4(PPh3)2 literature values. This is shown in Figure 25.
| Bond length | Measured values for Mo(CO)4(PCl3)2 ± 0.005 /Å | Literature values for Mo(CO)4(PPh3)2[6] |
| Mo-P | 2.42 | 2.500 |
| Mo-C | 2.06 | 2.005 |
| C-O | 1.17 | 1.16 |
| Bond angle | Measured ± 0.05 /° | Literature[6] |
| C-Mo-C (trans) | 180 and 178.4 | 180.0 |
| C-Mo-C (cis) | 89.2 and 90.8 | 92.1 |
| P-Mo-C | 90.0, 88.4 and 91.6 | 87.2 |
Figure 25: A table to compare structural parameters to literature value parameters for a similar complex
Comparison of the calculated parameters of Mo(CO)4(PCl3)2 with the literature values of Mo(CO)4(PPh3)2 shows the calculated parameters to be reasonable. The optimised complex is therefore a reasonable structure.
This calculation shows the trans isomer to be more stable than the cis isomer by 2.6 KJ mol-1. It is interesting to note that there is a disparity between this calculation and the previous calculation, which suggested that the cis isomer was more stable than the trans isomer by 2.6 KJ mol-1. For both calculations, the energy difference is still well within the order of error (10 KJ mol-1). This means no definitive conclusions can be drawn from these calculations as to which isomer is more stable. The small difference between the energies of the structural isomers suggests that there is a fine balance between cis and trans geometries of these complexes.
It is proposed that there are both steric and electronic contributions to stability. These two effects must be finely balanced between the two geometries for such a small energy difference to be seen.
Sterics: Significant steric clashes would be expected to exist in the cis-complex. These steric repulsions would be less severe in the trans complex and so the steric effect favours the trans isomer. It is important to note that this term could be reversed by introducing attractive interactions between ligands, which would favour the cis isomer.
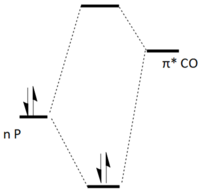
Electronic: It is proposed that a structural trans effect[7] exists in the cis-complex, which is not present in the trans-complex. This stabilises the cis-complex electronically. In the cis-complex, Mo-C bond lengths trans to phosphines are measured as 2.02Å ± 0.005. Mo-C bonds lengths cis to phosphines are measured as 2.05Å ± 0.005. In the trans complex, all M-C bond lengths are measured as 2.05Å ± 0.005. Whilst the trans effect is poorly understood, it can be inferred from bond lengths that there is some interaction between electron density on the phosphorous lone pair and the trans carbonyl ligands, which brings the carbonyl ligands in closer. An analogy can be drawn to synergistic bonding. It is important to note that it is highly unlikely that the phosphorous lone pair and the π* of a trans carbonyl ligand overlap directly due to the large distance between them, but some interaction must be present between these two orbitals, perhaps carried by metal based orbitals. This results in a stabilisation of the orbital bearing the lone pair and destabilisation of the unfilled carbonyl π*, resulting in electronic stabilisation of the complex as a whole. This is shown pictorially in Figure 26.
By varying the magnitudes of the steric and electronic components, one would expect to be able to tune the phosphine ligand to allow each structural isomer to be accessed. A rational design of the cis-complex is attempted in the following section.
Rational design?
Computational chemistry is often utilised in rational catalyst design. For instance, one structural isomer of a complex that is catalytically active may be more active than the other structural isomer. In order to maximise catalytic activity, the PR3 could be tuned in order to make one structural isomer dominate.
The trans isomer could be made to dominate easily by increasing the bulkiness of the R substituents, maximising steric repulsions in the cis isomer.
However, obtaining the cis isomer is more difficult and will be examined in more detail. The cis isomer could be achieved by increasing the electronic stabilisation of the cis isomer, whilst minimising sterics with a small, electron donating group. In order to further promote the cis isomer, attractive interactions between the two phosphine ligands could be implemented, for instance hydrogen bonding interactions or π stacking.
With this in mind, R = OH was modelled. It was imagined that hydrogen bonding interactions would exist between cis phosphines in the cis-complex, but would not be present in the trans-complex. Furthermore, structural trans-effects may exist with carbonyls trans to the electron donating phosphines. Finally, sterics were minimised with P(OH)3 being significantly smaller than PCl3 as shown in Figure 27.
The cis and trans Mo(CO)4(P(OH)3)2 complexes were optimised using DFT-B3LYP and a LANL2DZ basis set with added d orbitals for phosphorous. The output files were checked and a successful convergence was found for both isomers. The optimised structures are shown below. The summary of the optimisations is shown in Figure 28.
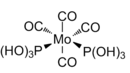 |
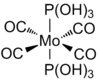 | |||
| Rational Design of a stable cis conformer | ||
| Cis | Trans | |
| D-Space | DOI:10042/to-7505 | DOI:10042/to-7506 |
| File type | .log | .log |
| Calculation Type | FOPT | FOPT |
| Calculation Method | RB3LYP | RB3LYP |
| Basis Set | LANL2DZ with added d orbitals for phosphorous | LANL2DZ with added d orbitals for phosphorous |
| E(RB+HF-LYP) | -989.063 Hatree ± 3.808x10-3 | -989.048 Hatree ± 3.808x10-3 |
| RMS Gradient Norm | 0.000 Hatree ± 3.808x10-3 | 0.000 Hatree ± 3.808x10-3 |
| Dipole moment | 5.06 debye ± 0.005 | 1.71 debye ± 0.005 |
| Point group | C1 | C1 |
| Job time | 6 hours 12 minutes 10.8 seconds | 8 hours 10 minutes 20.3 seconds |
Figure 28: A table to show the summary of the optimisations
In order to confirm the minima, frequency analysis was utilised. A summary of the frequency calculations is shown in Figure 29.
| Rational Design of a stable cis conformer | ||
| Cis | Trans | |
| D-Space | DOI:10042/to-7519 | DOI:10042/to-7522 |
| File type | .log | .log |
| Calculation Type | FREQ | FREQ |
| Calculation Method | RB3LYP | RB3LYP |
| Basis Set | LANL2DZ with added d orbitals for phosphorous | LANL2DZ with added d orbitals for phosphorous |
| E(RB+HF-LYP) | -989.063 Hatrees ± 3.808x10-3 | 989. 048 Hatree ± 3.808x10-3 |
| RMS Gradient Norm | 0.000 Hatree ± 3.808x10-3 | 0.00 Hatree ± 3.808x10-3 |
| Imaginary Frequencies | 0 | 0 |
| Dipole moment | 5.0582 debye ± 0.005 | 1.7142 debye ± 0.005 |
| Point group | C1 | C1 |
| Job time | 58 minutes 54.2 seconds | 57 minutes 20.0 seconds |
Figure 29: A table to show the summary of the frequency calculation
It was found that all frequencies were positive and thus a minima has been successfully converged to. The measured bond lengths (Mo-P ≈ 2.5Å and Mo-C ≈ 2Å) are reasonable in comparison to the previously established bond lengths - so plausible structures have been reached.
It can be seen that the cis isomer is 39.4 KJ mol-1 more stable than the trans isomer, so the objective of this exercise is achieved and the cis isomer is favoured significantly.
At the start of the exercise, the complex was designed with 3 features in mind:
- Minimise steric effects
- Maximise electronic effects
- Introduce attractive interactions between ligands to favour the cis
In order to evaluate how successful this design procedure has been, it's important to evaluate the resultant structures to see how many of these effects are operating. The stabilisation of the cis isomer could merely be the result of reduced sterics! Firstly, the electronic stabilisation will be examined.
In the cis-complex, Mo-C bond trans to phosphines are measured to have a bond length of 2.01Å ± 0.005. Then Mo-C bonds cis to phosphines are measured to have a bond length of 2.04Å ± 0.005. In the trans complex, all M-C bonds were measured to be 2.04Å ± 0.005. The shortening of Mo-C bonds trans to phosphines in the cis-complex is more severe when R = OH compared to when R = PCl3 (2.01Å cf 2.02Å). This suggests some success in trying to maximise this electronic stabilisation of the cis-complex. However, this reduction in bond length is very small, which suggests some improvement could be made here.
Secondly, the presence of hydrogen bonds is examined. It was intended to introduce hydrogen bonds between cis ligands, to stabilise the cis isomer. Hydrogen bonding distances are often between 1.8 and 2.6 Å [8] In the cis complex, there are two H-O interactions at a distance of 1.8Å bridging the two cis ligands, these are "external" to each phosphine. There are then two further "internal" interactions at a distance of 2.5Å within each phosphine. In the trans complex, there are only two "internal" hydrogen bonding interactions.
Frequency Analysis of Cis and Trans Mo(CO)4(PCl3)2
The IR frequencies were calculated using DFT-B3LYP and a LANL2-DZ basis set, with included d orbitals for the phosphorous atom and ultrafine electronic convergence conditions. Cis DOI:10042/to-7523 and Trans DOI:10042/to-7524
Low Frequency Vibrations
A number of vibrations were observed to have a low frequency, these are shown in Figure 30 (cis) and Figure 31 (trans).
Cis complex
| Stretching Mode # | Form of the vibration | Frequency (error in frequency) /cm-1 | Intensity |
| 1 |
|
12 (± 1) | 0 |
| 2 |
|
20 (± 2) | 20 |
| 3 |
|
46 (± 5) | 0 |
Figure 30: A table to show the low frequencies of the cis-complex
Trans complex
| Stretching Mode # | Form of the vibration | Frequency (error in frequency) /cm-1 | Intensity |
| 1 |
|
5 (± 0.5) | 0 |
| 2 |
|
7 (± 0.7) | 0 |
| 3 |
|
40 (± 4) | 0 |
Figure 31: A table to show the low frequencies of the trans complex'
It is noticed that all of the low frequency vibrations involve rotations about the Mo-P bonds. At room temperature (298.15 K), there is 2476 J mol-1 of energy (RT) available to the system. This corresponds to a wavenumber of around 207 cm-1. Vibrations and rotations which experience vibrations and rotations much lower than this value will be occur spontaneously at room temperature. This implies that the phosphine groups are freely rotating about the Mo-P bonds at room temperature in reality.
This explains why the point group of the structures has been incorrectly assigned as C1. Gaussian is not taking free rotation about Mo-P bonds into account when it is calculating the point group of the molecule and thus the symmetry is being broken by the 'static' phosphines. This leads to the C2 axis not being found in the cis complex and the C4 rotation axis not being found in the trans complex and thus an incorrect point group assignment in each case.
Carbonyl IR Stretches
From the calculated vibrational frequencies, the frequencies corresponding to carbonyl vibrations were found. The symmetry of the vibrations was assigned using a representation table as illustrated in Figure 9 previously.
Cis complex
| Stretching Mode # | Form of the vibration | Frequency (error in frequency) /cm-1 | Literature | Intensity | Symmetry |
| 42 |
|
1939 (± 194) | 1986 | 1599 | B2 |
| 43 | 1942 (± 194) | 1994 | 820 | B1 | |
| 44 | 1953 (± 195) | 2004 | 591 | A1 | |
| 45 | 2019 (± 20) | 2072 | 542 | A1 |
Figure 32: A table to show the CO stretches for the cis complex
Trans complex
| Stretching Mode # | Form of the vibration | Frequency (error in frequency) /cm-1 | Literature | Intensity | Symmetry |
| 42 |
|
1939 (± 194) | 1896 | 1605 | EU |
| 43 |
|
1940 (± 194) | 1896 | 1606 | EU |
| 44 |
|
1967 (± 197) | - | 6 | B1g |
| 45 |
|
2026 (± 203) | - | 5 | A1g |
Figure 33: A table to show the CO stretches for the cis complex
The point group of the cis complex is C2V. If stretching vectors are assigned along each CO bond, one can determine the number of expected normal stretching modes. A representation table is set up for the stretching vectors and is shown in Figure 34.
| C2v | E | C2 | σv (xy) | σv(xz) |
Γ  |
4 | 0 | 2 | 2 |
Figure 34 : The representation table for the cis complex
Using the reduction formula it is found that 2 stretches of A1 symmetry, one stretch of B1 symmetry and one stretch of B2 symmetry are expected. This is indeed what is observed computationally.
The same analysis is then applied to the trans complex. The point group of the trans complex is D4h. Again, stretching vectors are assigned along each CO bond. A representation table is set up for the stretching vectors Figure 35.
| D4h | E | 2C4 | C2 | 2C2' | 2C2'' | i | 2S4 | σh | 2σv | 2σd |
Γ  |
4 | 0 | 0 | 2 | 0 | 0 | 0 | 4 | 2 | 0 |
Figure 35 : The representation table for the trans-complex
Using the reduction formula it is found that 1 stretch of A1g, 1 stretch of B1g and 1 doubly degenerate stretch of EU symmetry are expected, again predicting 4 vibrations. However, the B1g and A1g stretches are totally symmetric, thus no change in dipole moment occurs throughout the vibration and so the totally symmetric vibrations will not be IR active. One would therefore expect 1 peak to be seen in the IR spectrum of EU symmetry corresponding to 2 degenerate vibrations.
4 calculated vibrational modes are seen. However the A1g and B1g vibrational modes are of very low intensity. The expected EU vibrations are degenerate and thus would give one peak in an IR spectrum. The reason for the A1g and B1g vibrations having a non-zero intensity is because the molecule has deviations from ideal bond angles. The C-Mo-C bond angles were not measured to be 90° as one would expect them to be, this leads to a small computed change in dipole moment for the A1g and B1g vibrations.
Mini project: Bent's rules applied to simple carbene systems
Introduction
In 1960, Bent proposed a rule in order to justify deviations in structures from VSEPR theory.[9] Bent's rule is a hybridisation argument that states:
"Atomic s character tends to concentrate in orbitals that are directed toward electropositive groups and atomic p character tends to concentrate in orbitals that are directed toward electronegative groups” [9]
Bent's rules have been applied to carbenes (Figure 36) and carbene like species in order to predict substituent effects on spin multiplicity. For a carbene substituted by electronegative substituents, the p character on the atomic carbon orbitals is directed towards the substituents, imparting a greater s character on the carbene electrons, leading to singlet carbenes. For a carbene substituted by electropositive substituents, the s character on the atomic carbon orbitals is directed towards the substituents, imparting a greater p character on the carbene electrons, leading to triplet carbenes.

Bent's rules are based on empirical observations and have little theoretical basis. The aims of this project are as follows:
- To recreate empirical observations in silico
- To use NBO analysis to examine if the hybridisation of the carbenes does change with electronegativity of substituents.
- To calculate the molecular orbitals of the system, to see if there is a Molecular Orbital basis for the observed trends.
- If possible, to provide a rationalisation of Bent's rules when applied to predictions of carbene spin multiplicity.
Optimisation of Structures
A series of structures of the type CR2 were optimised using DFT-B3LYP restricted-open shell calculations. The calculation was restricted to pair up α and β wavefunctions, as individual α and β wavefunctions are unfamiliar and would be difficult to interpret.
A 6-31G basis set is used to model most compounds. Less accurate basis sets have been previously used to calculate more complex systems, thus based on the limited experience gained throughout this lab, it is believed that the 6-31G basis set will suffice for the modelling of simple 3 atom carbene systems. Compounds containing second row elements are modelled with a 6-311G(d,p) basis set to account for the polarizability and diffusivity of orbitals on these second row elements. Figure 37 shows the optimised structures of the compounds.
| R | Basis Set | D-Space/Log file Singlet | D-Space/Log file Triplet | Energy of Singlet ± 3.808x10-3 / Hatree | Energy of Triplet ± 3.808x10-3 / Hatree | Structure Singlet | Structure Triplet |
| H | 6-31G | https://wiki.ch.ic.ac.uk/wiki/images/9/93/Bc608_CH2_SINGLET_GEO_OPT.LOG | https://wiki.ch.ic.ac.uk/wiki/images/3/32/Bc608_CH2_TRIPLET_GEO_OPT.LOG | -39.114 | -39.142 |
|
|
| SiH3 | 6-311G(d,p) | DOI:10042/to-7622 | DOI:10042/to-7623 | -620.605 | -620.641 |
|
|
| NH3+ | 6-31G | DOI:10042/to-7620 | DOI:10042/to-7621 | -150.287 | -150.296 |
|
|
| NH2 | 6-31G | https://wiki.ch.ic.ac.uk/wiki/images/4/41/BC608_NH2_GEOOPT_SINGLET.LOG | https://wiki.ch.ic.ac.uk/wiki/images/f/f7/Bc608_NH2_GEOOPT_TRIPLET.LOG | -149.919 | -149.798 |
|
|
| F | 6-31G | https://wiki.ch.ic.ac.uk/wiki/images/c/cf/Bc608_CF2_SINGLET_GEO_OPT.LOG | https://wiki.ch.ic.ac.uk/wiki/images/7/7d/Bc608_CF2_TRIPLET_GEOOPT.LOG | -237.625 | -237.552 |
|
|
| Br | 6-31G | https://wiki.ch.ic.ac.uk/wiki/images/1/14/Bc608_BR2_SINGLET_GEO_OPT.LOG | https://wiki.ch.ic.ac.uk/wiki/images/1/12/BC608_BR2_TRIPLET_GEO_OPT.LOG | -5181.112 | -5181.088 |
|
|
Figure 37: The optimised structures of the type CR2 using DFT-B3LYP and the indicated basis sets
All optimisations were found to converge to a stationary point.
Frequency Analysis to confirm a minima
In order to confirm the minima, the frequencies were calculated using the same basis sets as the optimisations. The results are shown in Figure 38.
| R | Basis Set | D-Space/Log file Singlet | D-Space/Log file Triplet | Low Frequencies singlet /cm-1 | Lowest 'real' frequency singlet /cm-1 | Low Frequencies triplet /cm-1 | Lowest 'real' frequency triplet /cm-1 | |
| H | 6-31G | DOI:10042/to-7624 | DOI:10042/to-7625 | -45, -43, -18, 0, 0, 0 | 1428 | 0, 0, 0, 16, 17, 33 | 1124 | |
| SiH3 | 6-311G(d,p) | DOI:10042/to-7626 | DOI:10042/to-7627 | -19, -9, -8, 0, 0, 2 | 114 | -6, -6, -5, 0, 0, 0 | 32 | |
| NH3+ | 6-31G | DOI:10042/to-7628 | DOI:10042/to-7629 | -22, -11, -11, 0, 0, 0 | 134 | -19 -6, 0, 0, 0, 3 | 114 | |
| NH2 | 6-31G | DOI:10042/to-7630 | DOI:10042/to-7632 | -14, 0, 0, 0 12, 24 | 520 | -768, -620, -474, -385, -13, 0 | 6.6 | |
| F | 6-31G | DOI:10042/to-7618 | DOI:10042/to-7619 | -27, -17, -15, 0, 0, 0 | 581 | - 10, 0, 0, 0 12, 13 | 464 | |
| Br | 6-31G | DOI:10042/to-7634 | DOI:10042/to-7635 | -40, -15, -11, 0, 0, 0 | 174 | -43, -11, 0, 0, 0, 6 | 166 |
Figure 38: The frequency analyses of the previously optimised structures
The frequency analysis was somewhat disappointing! The R = NH2 triplet showed worryingly negative low frequencies and a number of structures showed low frequencies outside the ideal 10 to -10 cm-1 range. Due to the approaching deadline and a big queue on SCAN, the structures to be modelled need to be reconsidered so that the project can be realistically achieved in the timeframe available. The effects of substituent electropositivity can be examined by going down group 17. The elements of group 17 also provide an added advantage of being typically monovalent in their bonding, thus avoiding complex structures. Furthermore, the low frequencies for these calculations were reasonable previously with a 6-31G basis set and should improve with a higher basis set. Most importantly, they can be modelled on desktop computers thus avoiding the SCAN queue.
Reoptimisation and frequency analysis using an improved basis set
A series of structures of the type CR2 were optimised using DFT-B3LYP restricted-open shell calculations with a 6-311++G(d,p) basis set. Figure 39 shows the optimised structures of the compounds.
| R | Log file Singlet | Log file Triplet | Energy of Singlet ± 3.808x10-3 / Hatree | Energy of Triplet ± 3.808x10-3 / Hatree | Structure Singlet | Structure Triplet |
| H | https://wiki.ch.ic.ac.uk/wiki/images/7/77/Bc608_improvedbasis_H_SINGLET_GEOOPT.LOG | https://wiki.ch.ic.ac.uk/wiki/images/8/8f/Bc608_improvedbasis_H_TRIPLET_GEOOPT.LOG | -39.147 | -39.164 |
|
|
| F | https://wiki.ch.ic.ac.uk/wiki/images/4/4f/Bc608_improvedbasis_F_SINGLET_GEOOPT.LOG | https://wiki.ch.ic.ac.uk/wiki/images/5/57/Bc608_improvedbasis_F_TRIPLET_GEOOPT.LOG | -237.774 | -237.690 |
|
|
| Cl | https://wiki.ch.ic.ac.uk/wiki/images/d/d1/Bc608_improvedbasis_CL_SINGLET_GEOOPT.LOG | https://wiki.ch.ic.ac.uk/wiki/images/3/3f/Bc608_improvedbasis_CL_TRIPLET_GEOOPT.LOG | -958.454 | -958.423 |
|
|
| Br | https://wiki.ch.ic.ac.uk/wiki/images/a/a0/Bc608_improvedbasis_BR_SINGLET_GEOOPT.LOG | https://wiki.ch.ic.ac.uk/wiki/images/5/53/Bc608_improvedbasis_BR_TRIPLET_GEOOPT.LOG | -5186.295 | -5186.270 |
|
|
Figure 39: Optimised structures of the type CR2 using DFT-B3lYP and a 6-311++G(d,p) basis set.
A frequency analysis was then performed on the optimised structures in order to confirm minima.
| R | D-Space/Log file Singlet | D-Space/Log file Triplet | Low Frequencies singlet /cm-1 | Lowest 'real' frequency singlet /cm-1 | Low Frequencies triplet /cm-1 | Lowest 'real' frequency triplet /cm-1 | |
| H | https://wiki.ch.ic.ac.uk/wiki/images/4/4c/Bc608_H_SINGLET_FREQ.LOG | https://wiki.ch.ic.ac.uk/wiki/images/b/b0/Bc608_H_TRIPLET_FREQ.LOG | -46, -38, -36, 0, 0, 0 | 1385 | 0, 0, 0, 47, 52, 53 | 1083 | |
| F | https://wiki.ch.ic.ac.uk/wiki/images/7/7b/Bc608_F_SINGLET_FREQ.LOG | https://wiki.ch.ic.ac.uk/wiki/images/7/73/Bc608_F_TRIPLET_FREQ.LOG | -36, -29, -21, 0, 0, 0 | 668 | -27, -22, -11, 0, 0, 0 | 509 | |
| Cl | https://wiki.ch.ic.ac.uk/wiki/images/4/43/Bc608_CL_SINGLET_FREQ.LOG | https://wiki.ch.ic.ac.uk/wiki/images/6/62/Bc608_CL_TRIPLET_FREQ.LOG | 0, 0, 0, 12, 12, 34 | 329 | - 15, -6, 0, 0, 0, 9 | 300 | |
| Br | https://wiki.ch.ic.ac.uk/wiki/images/c/c8/Bc608_BR_SINGLET_FREQ.LOG | https://wiki.ch.ic.ac.uk/wiki/images/7/73/Bc608_BR_TRIPLET_FREQ.LOG | 0, 0, 0, 3, 6, 7 | 190 | 0, 0, 0, 4, 7, 27 | 183 |
Figure 40: Frequency Analyses of the previously optimised structures.
As can be seen in Figure 40, the low frequencies were much more acceptable than the last set of calculations. The low frequencies were all at least an order of magnitude smaller than the lowest 'real' frequency in all cases. No negative frequencies were seen for the normal stretching modes confirming minima. The results of vibrational analyses are compared to literature in a later section. However, the analysis shows excellent agreement between calculated stretching frequencies and literature, so plausible optimised structures have been reached.
It can be seen that the triplet is favoured for the electropositive H substituent, whereas the singlet is favoured for the electronegative halogen substituents - as predicted by Bent's rules. Now the empirical observations have been recreated, an attempt will be made to understand why electronegativity affects spin multiplicity. Bent's rules are an argument based upon bond hybridisation, therefore an NBO analysis of the structures seems a logical place to start.
NBO Analysis
Core to Bent's rules is a hybridisation argument which is substituent electronegativity dependent. In order to test whether there is any basis to this argument, it would be desirable to calculate the hybridisation of the Natural Bond Orbitals in which the carbene electrons reside. The Natural Bond Orbitals of the singlets of CH2, CF2, CCl2 and CBr2 had been calculated in the previous frequency analyses.
Interestingly, NBO calculations imply that every singlet carbene modelled is ionic in character. No 2 centre - 2 electron bonding orbitals were found in the NBO analysis, denoted in the log file as "BD". Instead, all occupied orbitals are either core ("CR") or lone pair ("LP") orbitals, with higher orbitals being diffuse Rydberg ("Ry") orbitals.
Conversely, the triplet states of these carbenes showed bonding orbitals in all cases, with the Singularly Occupied Molecular Orbitals being a carbon orbital of 100% p character and another carbon based orbital of varying character referred to as "carbene orbital" here-on-in. Figure 40 shows higher NBO charges for the singlet when compared to the triplet, supporting the ionic bonding proposed in the singlet species.
| R | NBO charge on R in Singlet | NBO charge on C in Singlet | NBO charge on R in Triplet | NBO charge on C in Triplet |
| H | 0.527 | 2.946 | 0.113 | -0.226 |
| F | 4.335 | 3.331 | -0.345 | 0.690 |
| Cl | 8.530 | 2.940 | 0.070 | -0.140 |
| Br | 17.569 | 2.862 | 0.162 | -0.325 |
Figure 40: A comparison of NBO charges of CR2 fragments.

Whilst it is very interesting that the two different state multiplicities exhibit completely different bonding types, further calculations in which the Lewis structure is fixed would be required to try and understand why this is the case. Interpretation of the singlet NBO log files proved far too complex for a beginner to understand, with the expected "carbene orbital" not being found. Instead, 4 NBOs of varying character were seen. An example of these orbitals is shown in Figure 42.
12. (0.99553) LP*( 1) C 1 s( 73.70%)p 0.36( 26.21%)d 0.00( 0.09%)
0.0000 0.8580 0.0293 0.0002 0.0001
0.0000 0.0000 0.0000 0.0000 0.0000
0.0000 0.0000 0.0000 0.5102 0.0407
0.0110 -0.0022 0.0000 0.0000 0.0000
-0.0061 -0.0294
13. (0.44348) LP*( 2) C 1 s( 27.31%)p 2.65( 72.32%)d 0.01( 0.37%)
0.0000 0.5107 -0.1108 -0.0009 -0.0005
0.0000 0.0000 0.0000 0.0000 0.0000
0.0000 0.0000 0.0000 -0.8504 -0.0016
0.0109 0.0021 0.0000 0.0000 0.0000
-0.0413 0.0448
14. (0.37224) LP*( 3) C 1 s( 0.00%)p 1.00( 99.50%)d 0.01( 0.50%)
0.0000 0.0000 0.0000 0.0000 0.0000
0.0000 0.0000 0.0000 0.0000 0.9939
-0.0848 -0.0001 0.0008 0.0000 0.0000
0.0000 0.0000 0.0000 0.0000 -0.0706
0.0000 0.0000
15. (0.23875) LP*( 4) C 1 s( 0.00%)p 1.00( 99.52%)d 0.00( 0.48%)
0.0000 0.0000 0.0000 0.0000 0.0000
0.9968 0.0403 -0.0058 0.0068 0.0000
0.0000 0.0000 0.0000 0.0000 0.0000
0.0000 0.0000 0.0000 -0.0690 0.0000
Figure 42: Partially filled NBO orbitals where the carbene lone pair should occur.
Whilst the singlet NBO analysis proved complex, the hybridisation of triplet orbitals was much more straightforward. The hybridisation of triplet orbitals is examined in Figure 43.
| R | S character / % | P character /% |
| H | 33.98% | 66.02% |
| F | 63.59% | 36.39% |
| Cl | 59.17% | 40.81% |
| Br | 63.43% | 36.55% |
Figure 43: A comparison of hybridisation for the NBOs of triplet CR2 fragments.
From Figure 43 it would appear that Bent's hybridisation arguments are applicable. CH2 shows sp2 hybridisation, of the "carbene orbital", whereas more electronegative groups show increased s character. When this "carbene" orbital has high p character, it will be close in energy to the non-bonding carbon p orbital and thus the triplet state will be favoured. A high s character will stabilise the "carbene orbital" by bringing the electrons closer to the nucleus. This would increase the energy gap between the non bonding p orbital and the "carbene orbital". The spin pairing energy will then be smaller than the promotion energy and the singlet state will be favoured. This is shown in Figure 44.

IR Stretching frequencies of dihalocarbenes: A comparison of bond strengths
The lack of bonding interactions in the Natural Bond Orbital calculations of CR2 singlets was unexpected and the possibility of the modelled structures poorly reflecting reality was entertained. In order to see if the calculated bonds are reasonable, the vibrational spectra of the dihalo compounds are examined in detail. Unfortunately, due to the instability of the CH2 diradical, no literature vibrational frequencies or bond lengths could be found and the plausibility of the optimised structure could not be determined.
CCl2
| Stretching Mode # | Form of the vibration | Frequency (error in frequency) /cm-1 | Intensity | Symmetry within the C2V point group |
| 1 |
|
329 (± 33) | 1 | A1 |
| 2 |
|
709 (± 71) | 42 | A1 |
| 3 |
|
711 (± 71) | 429 | B1 |
Figure 44: A table to show the IR stretches of CCl2
Experimentally, 2 IR absorptions are observed at 748 and 721 cm-1[10]. The symmetric scissoring A1 stretch shows no change in dipole moment and thus is not observed experimentally. There is a very strong agreement between the calculated IR values and the literature IR values, suggesting that the optimised structure of CCl2 is reasonable.
CBr2
| Stretching Mode # | Form of the vibration | Frequency (error in frequency) /cm-1 | Intensity | Symmetry within the C2V point group |
| 1 |
|
190 (± 19) | 1 | A1 |
| 2 |
|
594 (± 59) | 18 | A1 |
| 3 |
|
624 (± 62) | 368 | B1 |
Figure 45: A table to show the IR stretches of CBr2
Experimentally, 2 IR absorptions are observed at 595 and 640 cm-1[11]. Again, the symmetric scissoring A1 stretch shows no change in dipole moment and thus is not observed experimentally. Again, there is a very strong agreement between the calculated IR values and the literature IR values, suggesting the optimisation of CBr2 has given a reasonable structure.
CF2
| Stretching Mode # | Form of the vibration | Frequency (error in frequency) /cm-1 | Intensity | Symmetry within the C2V point group |
| 1 |
|
668 (± 67) | 4 | A1 |
| 2 |
|
1086 (± 109) | 423 | B1 |
| 3 |
|
1209 (± 121) | 136 | A1 |
Figure 46: A table to show the calculated vibrational frequencies of CF2
No reports of the isolation or characterisation of diflurocarbene could be found, thus a direct comparison to literature bond lengths, angles or IR spectra is not possible. However, the stretching frequencies can be inferred from literature data for CCl2. C-F bonds will be stronger than C-Cl bonds due to increased overlap between fluorine valence orbitals and carbon valence orbitals, than between chlorine valence orbitals and carbon valence orbitals. One would therefore expect higher vibrational frequencies for difluorocarbene compared to the dichlorocarbene. Stretching frequencies in the 1000-1200 cm-1 range therefore seem reasonable, implying a reasonable structure of the CF2 carbene has been reached.
Molecular Orbital Examination of the Dihalocarbenes
Effects of electronegativity
The NBO analysis was not entirely successful in explaining Bent's rules and the analysis limited by the unexpected and interpretable singlet species results. The molecular orbitals were examined in order to see if they could provide any rationalisation of Bent's rules. Figure 47 shows the qualitative Molecular Orbitals of CF2 as determined by LCAO.

Figure 48: A table to compare calculated quantitative MOs for singlet CF2 with qualitative MOs
| R | HOMO-2 | HOMO-1 | HOMO | LUMO | HOMO-LUMO Gap / KJ mol-1 |
| F |  |
 |
 |
 |
535 |
| Cl | 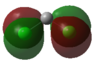 |
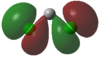 |
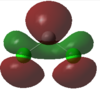 |
 |
365 |
| Br |  |
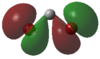 |
 |
 |
326 |
Figure 49: A table to compare the orbitals between the HOMO -2 and the LUMO for CF2, CCl2 and CBr2
Figure 49 shows a number of interesting points. Firstly, the HOMO-LUMO gap is decreasing as group 17 is descended. This is decreasing the promotion energy required to generate a triplet state. As the group is descended the elements become more electropositive and more sterically bulky. This is then in excellent agreement with Bent's rules, which state electropositive and bulky substituents give triplet carbenes.
Figure 49 also provides some indication as to why electronegativity of substituents effects spin multiplicity.
When two fragment orbitals (FOs) combine, they produce two molecular orbitals (MOs) - an in-phase, bonding combination of FOs and an out-of-phase antibonding combination of FOs. The relative contribution of each FO to each MO is determined by the FOs proximity in energy to the MO i.e. the closer in energy an FO is to an MO, the higher the contribution of that FO to that MO. Electronegative FOs are lower in energy than electropositive FOs. This means that a bonding MO will have an increased contribution from the more electronegative FO, whereas the corresponding antibonding MO will have an increased contribution from the more electropositive FO.
In the case of dichlorocarbenes, the HOMO is comprised of an antibonding combination of the carbon 2s orbital and a dihalogen FO derived from pZ orbitals (see Figure 48). The more electropositive the halogen, the higher in energy this dihalogen FO will be. It will therefore be closer in energy to the HOMO relative to an electronegative halogen. This leads to increased contribution from the dihalogen FO to the HOMO. This results in increased p character and diminished s character of the HOMO or "carbene orbital". The LUMO in all cases is derived from a dihalogen FO that was originally degenerate with the dihalogen FO that contributes to the HOMO.
The more electropositive the element is therefore, the more the HOMO and LUMO will resemble the unmixed dihalogen FOs and therefore the closer they will be in energy. They will be closer in energy because the dihalogen FOs being degenerate in the unmixed state, thus the HOMO-LUMO gap decreases.
Effects of sterics
It is proposed that bulky substituents will make the molecule more linear due to steric repulsion between substituents. Unfortunately, Bromine was not bulky enough to cause sufficient linearisation of the molecule for the energy ordering of the molecular orbitals to change significantly enough for the triplet to be favoured. However, a Walsh correlation diagram can be used to imagine what would happen to the ordering of the molecular orbitals upon the molecule becoming more linear. This is shown in Figure 50.
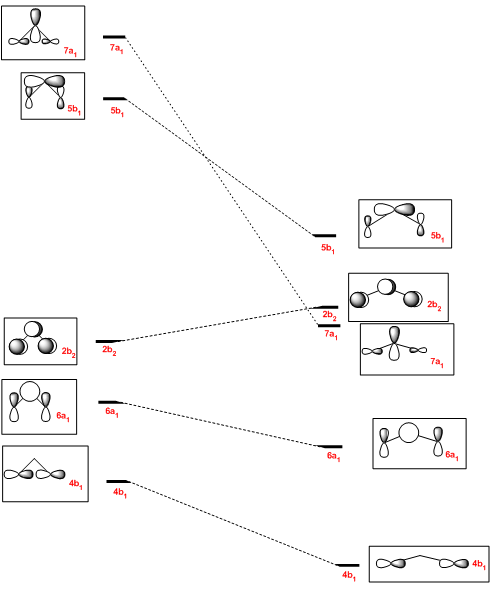
It can be seen that the formerly very antibonding 7a1 molecular orbital has become relatively non-bonding upon linearisation, making this orbital become the new HOMO. The LUMO, 2b2 remains the LUMO, but is increased in energy due to diminished constructive overlap between the two pZ orbitals in the R2 fragment. The former HOMO, 6a1 orbital becomes less antibonding upon linearisation and is lowered in energy to become the HOMO-1. Antibonding interactions in the 4b1 are also reduced, by increasing the distance between pX orbitals in the R2 fragment. The HOMO and LUMO will be very close in energy and thus promotion will be preferred over spin pairing, thus the triplet is favoured for structures showing more linear behaviour.
Further calculations using bulky substituents such as tertiary butyl or SiMe3 would be required to confirm this effect. Unfortunately, there was insufficient time to perform these calculations within this report.
Conclusion of the mini project
In conclusion, the empirically observed spin multiplicity of substituted carbenes has been recreated in silico. Interestingly, NBO analysis indicates that singlet carbenes are mostly ionic in their bonding, whereas triplet species have more covalent character. The cause of these observed differences however remains elusive. Further work in this area is required.
The main initial aim of this work was to propose a rationalisation of Bent's rules applied to simple carbene systems and this has been achieved.
Electronegative substituents have a small contribution to the HOMO, leading to a high s character at the carbon centre and a large HOMO-LUMO gap, which favours spin pairing over electron promotion, resulting in singlet carbenes.
Electropositive substituents have a greater contribution to the HOMO, leading to high p character at the carbon centre and a small HOMO-LUMO gap, which favours electron promotion over spin pairing, resulting in triplet carbenes.
However, it is important to note that these arguments only apply to substituents with valence p orbitals. The effects of d orbital participation has also not been considered, which may or may not be significant.
Sterically large substituents are proposed to alter the energy ordering of molecular orbitals and change the HOMO and LUMO to orbitals derived from degenerate orbitals of the substituent fragment orbitals. This decreases the HOMO-LUMO gap and favours the triplet. However, further calculations are required to support this proposal.
References
- ↑ K. Burke, J. Werschnik and E.K.U. Gross, Journal of Chemical Physics 2005, 123, 123-131 DOI:10.1063/1.1904586
- ↑ P. Hunt, Inorganic Computational Chemistry Year 4 lecture materials 2011, Imperial College London
- ↑ M.R. Hartman, J.J. Rush, T.J. Udovic, R.C. Bowman and S.J. Hwang, Jounral of Solid State Chemistry 2007, 180, 1298-1305 DOI:10.1016/j.jssc.2007.01.031
- ↑ A. Eschenmoser, D. Felix and G. Ohloff , Helvetica Chimica Acta 1967, 50, 708-713 DOI:doi:10.1002/hlca.19670500232
- ↑ J. Glaser and G. Johansson, Acta Chemica Scandinavica 1982, 36a, 125-135 DOI:10.1021/jp0124802
- ↑ 6.0 6.1 G. Hogarth and T. Norman, Inorganic Chemistry Acta 1997, 254, 167 {{DOI|10.1016/S0020-1693(96)05133-X|}
- ↑ B.J. Coe, S.J. Glenwright, Coordination Chemistry Reviews 2000, 203, 5-80DOI:10.1016/S0010-8545(99)00184-8
- ↑ L. Benco, D. Tunega, J. Hafner and H. Lischka, Journal of Physical Chemistry B 2001, 105, 10812-10817DOI:10.1021/jp0124802
- ↑ 9.0 9.1 H.A. Bent, Chemical Reviews 1961, 61, 275-311 DOI:10.1021/cr60211a005
- ↑ D.E. Milligan and M.E. Jacox, The Journal of Chemical Physics 1967, 47, 703-707 DOI:10.1063/1.1711942
- ↑ L. Andrews and T. Granville Carver, The Journal of Chemical Physics 1968, 49, 896-902 DOI:10.1063/1.1670158