BPE IEM15
NH3
Optimisation analysis
Calculation Method: RB3LYP
Basis set: 6-31G(d,p)
E(RB3LYP): -56.5577683 a.u.
RMS Gradient Norm: 0.00000485 a.u.
Point group: C3V
Optimised bond length: 1.01798 Angstrom
Optimised bond angle: 105.471 degrees
| Item | Value | Threshold | Converged? | |
|---|---|---|---|---|
| Maximum | Force | 0.000004 | 0.000450 | YES |
| RMS | Force | 0.000004 | 0.000300 | YES |
| Maximum | Displacement | 0.000072 | 0.001800 | YES |
| RMS | Diplacement | 0.000035 | 0.001200 | YES |
NH3 molecule |
The optimisation file is linked here
Vibrational analysis
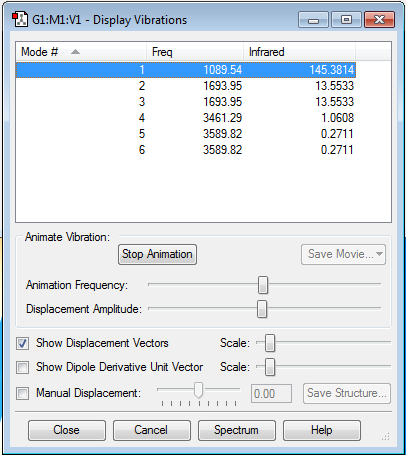
Q1) How many modes do you expect from the 3N-6 rule? (3x4)-6 = 6 modes
Q2) Which modes are degenerate? Modes 2 & 3 and 5 & 6
Q3) Which modes are "bending" vibrations and which are "bond stretch" vibrations? Modes 1, 2, and 3 are bending vibrations. Whereas, modes 4, 5, and 6 are stretching vibrations.
Q4) Which mode is highly symmetric? Mode 4
Q5) One mode is known as the "umbrella" mode, which one is this? Mode 1
Q6) How many bands would you expect to see in an experimental spectrum of gaseous ammonia? 4 bands
Charge analysis
The charge on the nitrogen atom is -1.125 and the charge on the hydrogen atom is 0.375. The nitrogen atom being negatively charged and the hydrogen atom being positively charged is expected because the nitrogen atom is more electronegative (3.04 compared to 2.1) so draws the electrons onto it from the hydrogen atom thus giving it a negative charge and the hydrogen atom a positive charge.
N2
Optimisation analysis
Calculation Method: RB3LYP
Basis set: 6-31G(d,p)
E(RB3LYP): -109.52412868 a.u.
RMS Gradient Norm: 0.00000060 a.u.
Point group: D*H
Optimised bond length: 1.10550 Angstrom
| Item | Value | Threshold | Converged? | |
|---|---|---|---|---|
| Maximum | Force | 0.000001 | 0.000450 | YES |
| RMS | Force | 0.000001 | 0.000300 | YES |
| Maximum | Displacement | 0.000000 | 0.001800 | YES |
| RMS | Diplacement | 0.000000 | 0.001200 | YES |
N2 molecule |
The optimisation file is linked here
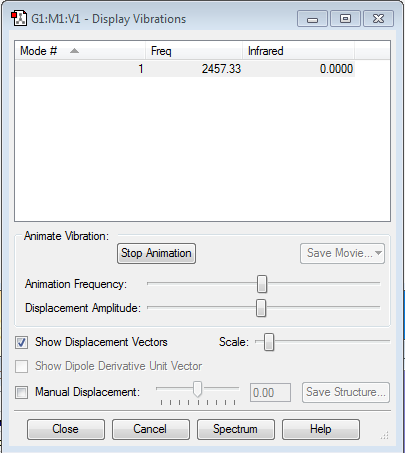
Vibrational analysis
H2
Optimisation analysis
Calculation Method: RB3LYP
Basis set: 6-31G(d,p)
E(RB3LYP): -1.178353936 a.u.
RMS Gradient Norm: 0.00000017 a.u.
Point group: D*H
Optimised bond length: 0.74279 Angstrom
| Item | Value | Threshold | Converged? | |
|---|---|---|---|---|
| Maximum | Force | 0.000000 | 0.000450 | YES |
| RMS | Force | 0.000000 | 0.000300 | YES |
| Maximum | Displacement | 0.000000 | 0.001800 | YES |
| RMS | Diplacement | 0.000001 | 0.001200 | YES |
H2 molecule |
The optimisation file is linked here
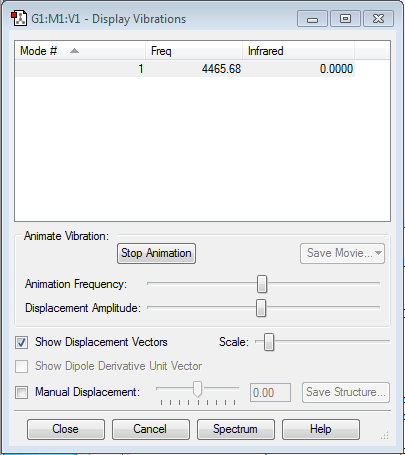
Vibrational analysis
Reactivity
Ammonia can be produced industrially by converting nitrogen gas and hydrogen gas in the Haber-Bosch process:
3H2 + N2 -> 2NH3
E(NH3)= -56.5577683 a.u.
2*E(NH3)= -113.1155366 a.u.
E(N2)= -109.52412868 a.u.
E(H2)= -1.178353936 a.u.
3*E(H2)= -3.535061808 a.u.
ΔE=2*E(NH3)-[E(N2)+3*E(H2)]= -0.056346112 a.u. = -147.9367283252 kJ/mol
This suggests that the ammonia product is thermodynamically more stable.
H2SiO
Optimisation analysis
Calculation Method: RB3LYP
Basis set: 6-31G(d,p)
E(RB3LYP): -365.90001403 a.u.
RMS Gradient Norm: 0.00000941 a.u.
Point group: CS
Optimised Si-H bond length: 1.48652 Angstrom
Optimised Si=O bond length: 1.53172 Angstrom
Optimised H-Si=O bond angle: 124.158 degrees
Optimised H-Si-H bond angle: 111.686 degrees
The bond lengths and angles given by this optimisation can be compared to some expermental values[1]:
Experimental Si-H bond length: 1.472 Angstrom
Experimental Si=O bond length: 1.515 Angstrom
Experimental H-Si-H bond angle: 112.000 degrees
These are all reasonably close to the corresponding value given by the optimisation with the differences arising because of a potential lack of need to take into consideration by GaussView of the experimental conditions.
| Item | Value | Threshold | Converged? | |
|---|---|---|---|---|
| Maximum | Force | 0.000023 | 0.000450 | YES |
| RMS | Force | 0.000009 | 0.000300 | YES |
| Maximum | Displacement | 0.000023 | 0.001800 | YES |
| RMS | Diplacement | 0.000017 | 0.001200 | YES |
H2SiO molecule |
The optimisation file is linked here
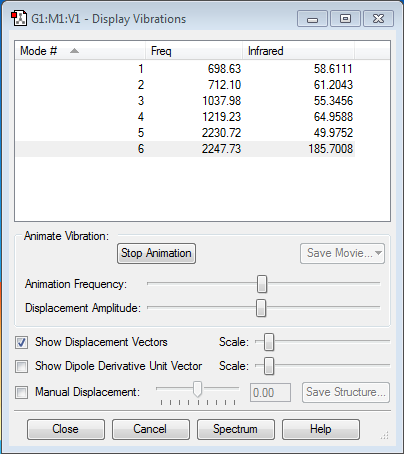
Vibrational analysis
As dictated by the 3N-6 rule I expected 6 vibrational modes, which is what happened. Modes 1-3 are bending modes, whereas, modes 4-6 are stretching modes. There are no degenerate modes, which could be because of there being two different substituents present, This means that one would expect 6 bands in an IR spectrum of this molecule because all of the modes are IR active. Mode 4 is an Si=O stretch which can be compared to an experimental value of 1202 cm-1[2]. Mode 1 is an SiH2 deformation which can be compared to a literature value of 697 cm-1[2].
Charge analysis
The charge on the silicon atom is 1.472, the charge on the hydrogen atoms is -0.236, and the charge on the oxygen atom is -1.001. This is expected because the oxygen and hydrogen atoms are more electronegative than the silicon atom (3.44 and 2.1 compared to 1.9) so the electrons are drawn onto them from the silicon atom thus giving them a negative charge and the silicon atom a positive charge. The oxygen atom is the most negatively charged because it is more electronegative than hydrogen.
Molecular Orbitals
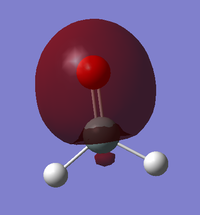
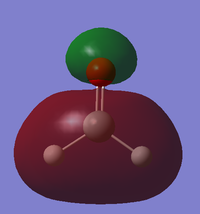
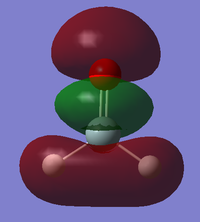
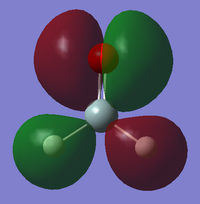
This MO is formed from the 2s AO on the oxygen and the 3s AO on the silicon with some p character present as well as shown by the nodal plane. It is a mostly bonding MO with some antibonding present because of the p orbital character. It is quite high in energy with an energy of -0.92465. It is occupied and will contribute to the sigma bond between the silicon and oxygen. This bond is heavily polarised to the oxygen due to it being a lot more electronegative so the electron density of this orbital is mostly over the oxygen.
This MO is formed from the 2s AO on the oxygen and the 3s AO on the silicon and also from the 1s AOs on the hydrogen atoms. It is a bonding MO between the hydrogen and silicon atoms but it is antibonding between the silicon and oxygen atoms. It is higher in energy than the previous orbital with an energy of -0.52699, this is probably because it has more antibonding character. It is occupied and contributes to the sigma bonds between the silicon and hydrogen atoms.
This MO is formed from the p orbitals of the oxygen and silicon atoms that is along the bond. It is a bonding MO, is occupied and contributes to the the sigma bond between the oxygen silicon atoms. It is higher in energy than the previous orbitals with an energy of -0.35346 which is because the p orbitals are higher in energy than s orbitals to begin with so the MOs formed will also tend to be higher in energy.
This MO is formed from a p orbital on the oxygen atom, the s orbitals on the hydrogen atoms and has a bit of d orbital character originating from the silicon atom which would be in phase with the other orbitals. This is the HOMO and has a high energy of -0.28497. It is mostly nonbonding but will partially contribute to the sigma bonds between the hydrogen and silicon atoms and to the pi bond between the silicon and oxygen atoms.
This MO is formed from a p AO on both the silicon and oxygen atoms. It is an antibonding orbital and is the LUMO with an energy of -0.7728.
Formation
This molecule can be formed by isolating ozong and then producing O2 and O(1D) through photolysis. The latter product reacts readily with SiH4 to give an excited species, which decomposes to H2SiO[2]:
SiH4 + O(1D) -> [SiH4O]* -> H2 + H2SiO