At3815

In Introduction to Molecular Modelling 2, the use of GaussView 5.0 is used to obtain information and establish optimised structures of various species, and to investigate the transitions states and intermediates that cannot be observed by a chemical reaction. In this lab, an investigation of the NH₃ Molecule was carried out and the following data was obtained.

NH₃ Molecule

Optimisation of molecule

NH₃ Molecule

Optimised NH3 molecule

More Info

Calculation Method

RB3LYP

Basis Set

6-31g(d,p)

Final Energy

-56.55776873 a.u.

RMS Gradient

0.00000485 a.u.

Point Group

C_3v

Bond Length (N-H): 1.01798Å

Bond Angle (H-N-H): 105.741°

         Item               Value     Threshold  Converged?
 Maximum Force            0.000004     0.000450     YES
 RMS     Force            0.000004     0.000300     YES
 Maximum Displacement     0.000072     0.001800     YES
 RMS     Displacement     0.000035     0.001200     YES

 Predicted change in Energy=-5.986298D-10
 Optimization completed.

The optimisation file is linked to here.

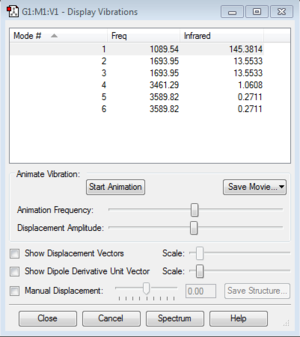
Display Vibrations


Vibrations
NH3 molecule has 6 vibration modes.
Expected number of modes	3(4)-6= 6
Degenerate modes	2 & 3; 5 & 6
Bending vibrations	4, 5, 6
Highly symmetric modes	4
Number of bands expected to see in experimental spectrum of NH3 (g)	2

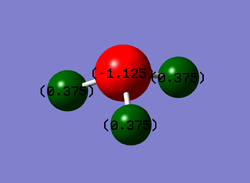
Charge Analysis

Due to a higher electronegativity in nitrogen atom compared to hydrogen atom, a negative charge is expected for the N atom and a positive charge for the H atom.

Reaction Energies

H₂ Molecule

Optimisation of Molecule

H₂ Molecule

Optimised H2 molecule

More Info

Calculation Method

RB3LYP

Basis Set

6-31g(d,p)

Final Energy

-1.17853936 a.u.

RMS Gradient

0.00000017 a.u.

Point Group

D_∞h

Bond Length (H-H): 0.74279Å

         Item               Value     Threshold  Converged?
 Maximum Force            0.000000     0.000450     YES
 RMS     Force            0.000000     0.000300     YES
 Maximum Displacement     0.000000     0.001800     YES
 RMS     Displacement     0.000001     0.001200     YES
 Predicted change in Energy=-1.164080D-13
 Optimization completed.

The optimisation file is linked to here.

Display Vibrations

N₂ Molecule

Optimisation of Molecule

N₂ Molecule

Optimised N2 molecule

More Info

Calculation Method

RB3LYP

Basis Set

6-31g(d,p)

Final Energy

-109.52412868 a.u.

RMS Gradient

0.00000060 a.u.

Point Group

D_∞h

Bond Length (N-N): 1.10550Å

         Item               Value     Threshold  Converged?
 Maximum Force            0.000001     0.000450     YES
 RMS     Force            0.000001     0.000300     YES
 Maximum Displacement     0.000000     0.001800     YES
 RMS     Displacement     0.000000     0.001200     YES
 Predicted change in Energy=-3.401111D-13
 Optimization completed.

The optimisation file is linked to here.

Display Vibrations

Haber-Bosch process

The energy for the reaction of N₂ + 3H₂ -> 2NH₃ can be calculated using the below energies.

- E(NH3)= -56.55776873 a.u.

- 2*E(NH3)= -113.11553746 a.u.

- E(N2)= -109.52412868 a.u.

- E(H2)= -1.17853936 a.u.

- 3*E(H2)= -3.53561808 a.u.

- ΔE=2*E(NH3)-[E(N2)+3*E(H2)]= -0.05579070 a.u.= -146.47 kJ/mol

Since ΔE is negative which shows that the forward reaction is exothermic, the ammonia product is more stable than the gaseous reactants.

PH₅ Molecule

The small molecule I have chosen for investigation is phosphorane, PH₅ which adopts a trigonal bipyramidal molecular geometry. A similar type of analysis using GaussView 5.0 was carried out for PH₅ as with NH₃ and the following information was obtained.

Optimisation of Molecule

PH₅ Molecule

Optimised PH5 molecule

More Info

Calculation Method

RB3LYP

Basis Set

6-31g(d,p)

Final Energy

-344.25491049a.u.

RMS Gradient

0.00000471 a.u.

Point Group

D_3h

The optimisation file is linked to here.

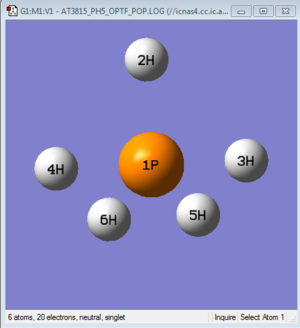
Bond Lengths (P-2H, P-5H, P-6H): 1.43316Å ; (P-3H, P-4H): 1.48687Å

Bond Angles (2H-P-3H, 2H-P-4H, 3H-P-6H, 4H-P-5H) = 90° ; (5H-P-6H) = 120°

Display Vibrations

It can be seen that PH₅ has 12 vibration modes. However, there are only 8 distinct frequencies. There are 4 pairs of degenerate modes: 1 & 2, 4 & 5, 6 & 7 and 11 & 12. In the IR spectrum, only 4 distinct bands can be observed as the intensities for mode 1, 2, 6, 7, 8 and 10 are zero or too low to be observed. Modes 1 to 7 are "bending" vibrations while modes 8 to 12 are "bond stretch" vibrations.

Charge Analysis

As phosphorous is less electronegative than hydrogen, the phosphorous atom is expected to carry a positive charge while the neighbouring hydrogen atoms carry a negative charge. Since PH₅ is a neutral molecule, the sum of the partial negative charges on all the hydrogens are similar to the partical positive charge on phosphorous.

Molecular Orbitals

Molecular Orbital	Energy/a.u.	Comments
	-77.14583	MO1 shows the 1s atomic orbital surrounding the central phosphorous atom. The energy is significantly lower than the rest of the atomic orbitals of P. Due to the difference in energies between the 1s AO of P and the 1s AO of H, this results in a non-bonding molecular orbital. (The 2s and 2p atomic orbitals of P are also too low in energy to interact with hydrogen atomic orbitals.)
	-0.68487	MO6 shows the first (lowest energy) bonding molecular orbital. It is contributed by the 1s orbitals of the 5 hydrogen atoms and the 3s orbital of the phosphorous atom.
	-0.42682	MO7 (shown), MO8 and MO9 shows the bonding molecular orbitals contributed by the 3p atomic orbitals of phosphorous and 1s atomic orbitals of hydrogen. MO7 and MO8 are contributed by 3px and 3py AOs of P respectively with the 1s AO of the equatorial hydrogens, and are degenerate. MO9 is contributed by 3pz AO of P and 1s AO of the axial hydrogens. MO9 is of a higher energy level than MO7 and MO8 with an energy level of -0.40948 a.u.
	-0.21463	MO10 is contributed by the 5 1s hydrogen AOs. There is no interactions with the atomic orbitals of P and thus is a non-bonding orbital. The diagram shows that the equatorial and axial hydrogens are in different phases. This filled MO has the highest energy, and thus represents the HOMO.
	0.4278	MO11, MO12 (shown) and MO13 shows the anti-bonding molecular orbitals of MO8, MO7 and MO9 respectively. MO11 and MO12 are degenerate and MO13 has a higher energy level of 0.05435 a.u. MO11 is the lowest energy anti-bonding MO, and thus is the LUMO.

Further Analysis of PH₅ Molecule

Through running the structure of PH₃ through GaussView 5.0, the following information was gathered about the molecule.

PH₃ Molecule

Optimised PH3 molecule

More Info

Calculation Method

RB3LYP

Basis Set

6-31g(d,p)

Final Energy

-343.14506758a.u.

RMS Gradient

0.00009144 a.u.

Point Group

C_3v

The geometry of PH₃ is similar to NH₃ with a pyramidal shape.

From the information of PH₃ gathered, the energy of the formation of PH₅ through the reaction of PH₃ + H₂ -> PH₅ can be calculated using the following energies.

- E(PH5)= -344.25491049a.u.

- E(H2)= -1.17853936 a.u.

- E(PH3)=-343.14506758a.u.

- ΔE=E(PH5)-[E(PH3)+E(H2)]= 0.06869645 a.u.

As ΔE is positive, this shows that the formation of PH₅ is endothermic and that the product is of a higher energy than the reactants, thus PH₅ is not a stable molecule and generally does not exist.

On the other hand, other bipyramidal phosphorane molecules such as PF₅ is a more stable molecule with a much lower energy of -840.67634601 a.u.

NH3 Molecule

Optimisation of molecule

Display Vibrations

Charge Analysis

Reaction Energies

H2 Molecule

Optimisation of Molecule

Display Vibrations

N2 Molecule

Optimisation of Molecule

Display Vibrations

Haber-Bosch process

PH5 Molecule

Optimisation of Molecule

Display Vibrations

Charge Analysis

Molecular Orbitals

Further Analysis of PH5 Molecule

NH₃ Molecule

H₂ Molecule

N₂ Molecule

PH₅ Molecule

Further Analysis of PH₅ Molecule