Am8616-inorganic
PLEASE READ! I have realised very late on into the lab that when i've done the frequency analysis for all the molecules shown, instead of adding "pop=full" into the additional comments, i deleted what was already there which was "integral=grid=ultrafine" and replaced this with "pop=full". After conferring with the lab demonstrator, it was identified that this is the source of why the energies for my optimised molecules and the energies after the frequency analysis were not the same allowing a variation in the last two digits. However, some molecules still did have equal energies. Despite this, at every stage all the item tables showed that everything had converged and all frequencies were positive.
BH3 molecule optimisation and analysis
RB3LYP/6-31G(d,p)
Item Value Threshold Converged? Maximum Force 0.000203 0.000450 YES RMS Force 0.000098 0.000300 YES Maximum Displacement 0.000867 0.001800 YES RMS Displacement 0.000415 0.001200 YES
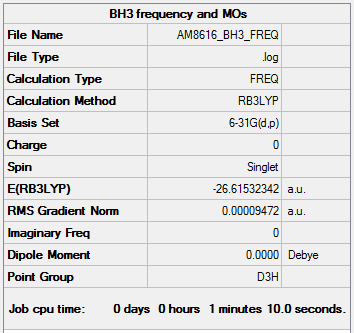
Frequency analysis log file AM8616_BH3_FREQ
Low frequencies --- -0.2262 -0.1036 -0.0056 48.0011 49.0614 49.0619 Low frequencies --- 1163.7216 1213.6709 1213.6736
test molecule |
| wavenumber (cm-1) | Intensity (arbitrary units) | symmetry | IR active? | type |
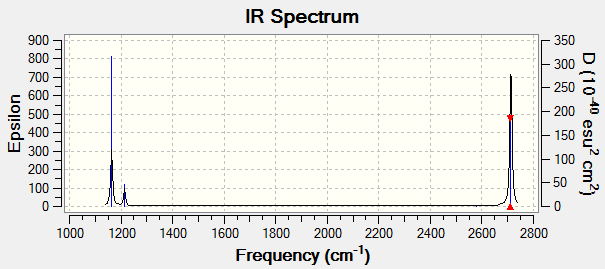
| 1164 | 92 | A2 | yes | out-of-plane bend |
| 1214 | 14 | E' | very slight | bend |
| 1214 | 14 | E' | very slight | bend |
| 2580 | 0 | A1' | no | symmetric stretch |
| 2713 | 126 | E' | yes | asymmetric stretch |
| 2713 | 126 | E' | yes | asymmetric stretch |
Although there are 6 vibrational modes, only three peaks can be seen on the IR spectrum of BH3. This is due to one peak being IR inactive (Intensity = 0), therefore this vibrational mode is not seen on the IR spectrum. Also, some of the vibrational modes are degenerate (same energy), therefore only one peak will be seen on the IR spectrum as they stretch/bend at the same frequency. For example, for bh3 the two bend modes are degenerate and so are the asymmetric stretches. This results in overall there only being three peaks.
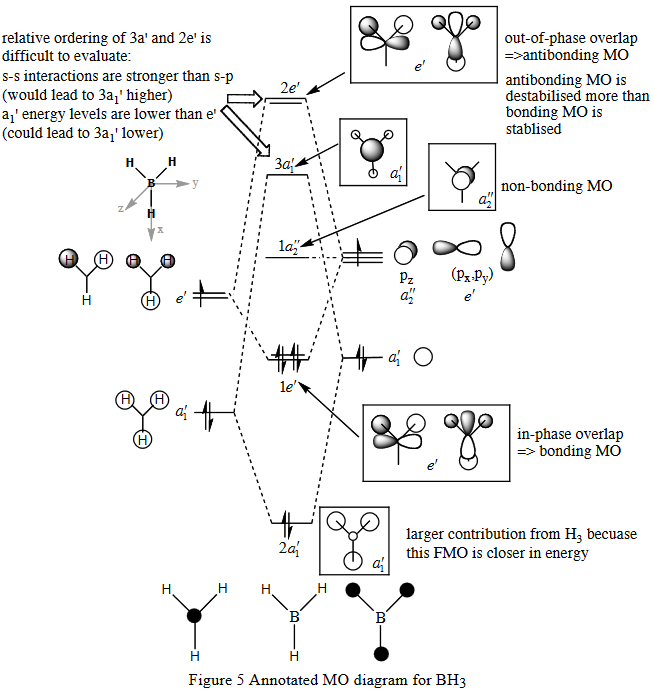
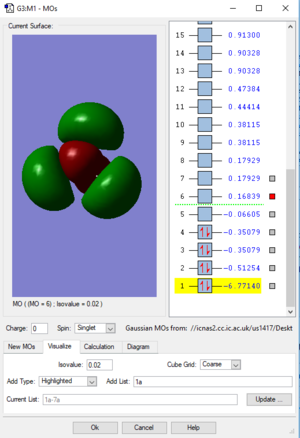
| 2a'1 | 1e' | 1a2 | 3a'1 | 2e' |
 |
  |
 |
 |
  |
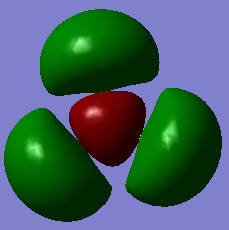NH3 molecule optimisation and analysis
RB3LYP/6-31G(d,p)
Item Value Threshold Converged? Maximum Force 0.000006 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000012 0.001800 YES RMS Displacement 0.000008 0.001200 YES
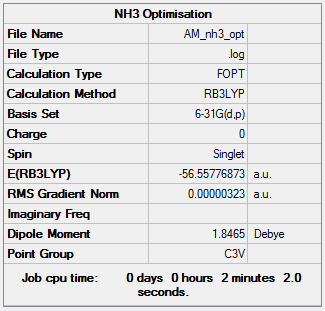
Frequency analysis log file AM8616_NH3_FREQ
Low frequencies --- -8.5646 -8.5588 -0.0047 0.0454 0.1784 26.4183 Low frequencies --- 1089.7603 1694.1865 1694.1865
test molecule |
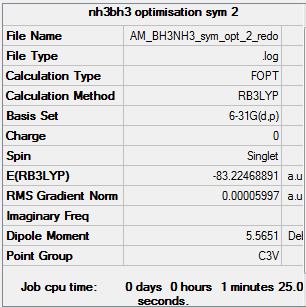
BH3NH3 molecule optimisation and analysis
RB3LYP/6-31G(d,p)
Item Value Threshold Converged? Maximum Force 0.000122 0.000450 YES RMS Force 0.000058 0.000300 YES Maximum Displacement 0.000531 0.001800 YES RMS Displacement 0.000296 0.001200 YES
Frequency analysis log file AM8616_NH3BH3_FREQ
Low frequencies --- -0.0617 -0.0457 -0.0067 21.6818 21.6878 40.5525 Low frequencies --- 266.0206 632.3610 640.1375
test molecule |
BH3NH3 Dative Bond Strength
E(NH3)= -56.55777 au E(BH3)= -26.61532 au E(NH3BH3)= -83.22469 au
ΔE=E(NH3BH3)-[E(NH3)+E(BH3)] = -83.22469 - [-56.55777-26.61532]
=-0.0516 au = -0.0516/0.0004 Kjmol-1 =-129 Kjmol-1
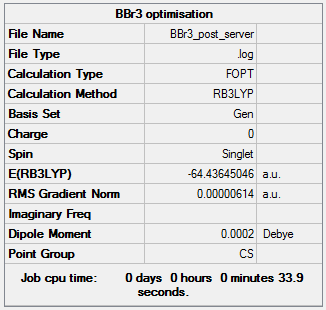
BBr3 Optimisation
RB3LYP/Gen
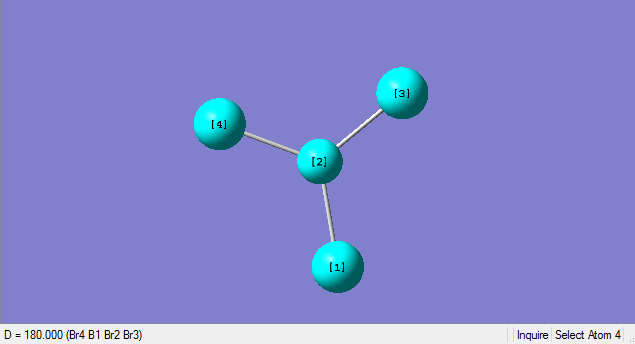
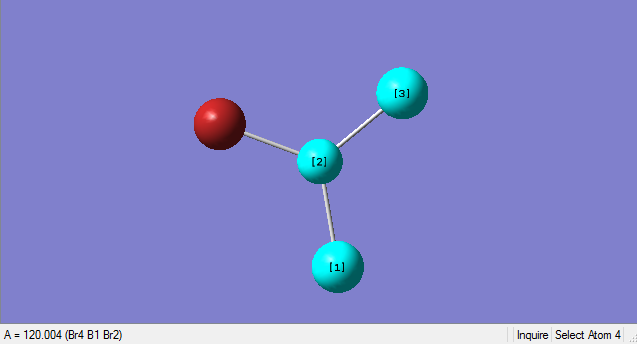
As can be seen from the summary table, the optimised BBr3 molecule has a point group of CS. However, this is not the true point group of BBr3, it should be D3H. Analysing the optimised molecule, the dihedral angle can be seen to be 180o which is correct, but the bond angle is 120.004o. This slight deviation from 120o means that the D3H symmetry has been broken to the CS symmetry. After conferring with the demonstrator, i was advised to carry on as the item tables showed everything had converged and the frequencies were all positive.
Item Value Threshold Converged? Maximum Force 0.000010 0.000450 YES RMS Force 0.000007 0.000300 YES Maximum Displacement 0.000045 0.001800 YES RMS Displacement 0.000032 0.001200 YES
Frequency analysis log file AM8616 BBR3 FREQ
Low frequencies --- -1.9018 -0.0002 0.0001 0.0002 1.5796 3.2831 Low frequencies --- 155.9053 155.9625 267.7047
test molecule |
Aromaticity Project
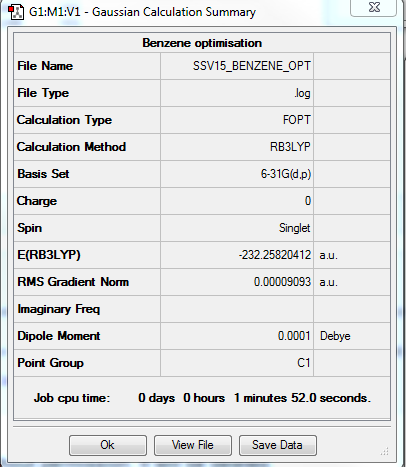
Benzene Optimisation and Frequency Analysis
RB3LYP/6-31G(d,p)
Item Value Threshold Converged? Maximum Force 0.000198 0.000450 YES RMS Force 0.000082 0.000300 YES Maximum Displacement 0.000849 0.001800 YES RMS Displacement 0.000305 0.001200 YES
Frequency analysis log file AM8616_Benzene_FREQ
Low frequencies --- -2.1456 -2.1456 -0.0088 -0.0041 -0.0040 10.4835 Low frequencies --- 413.9768 413.9768 621.1390
test molecule |
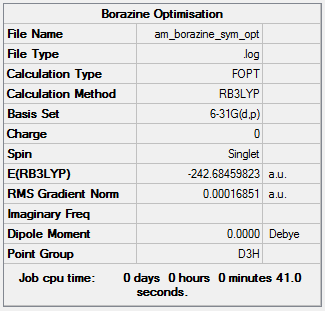
Borazine Optimisation and Frequency Analysis
RB3LYP/6-31G(d,p)
Item Value Threshold Converged? Maximum Force 0.000166 0.000450 YES RMS Force 0.000076 0.000300 YES Maximum Displacement 0.000679 0.001800 YES RMS Displacement 0.000249 0.001200 YES
Frequency analysis log file AM BORAZINE FREQ
Low frequencies --- -11.9009 -11.5537 -7.0446 -0.0106 0.0475 0.0879 Low frequencies --- 289.2479 289.2558 403.9297
test molecule |
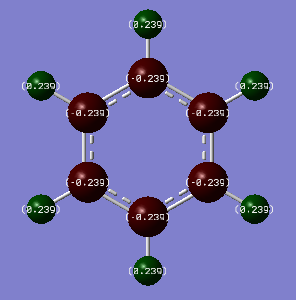
Benzene and Borazine Charge Analysis
| Benzene | Borazine | |
|---|---|---|
 |
 |
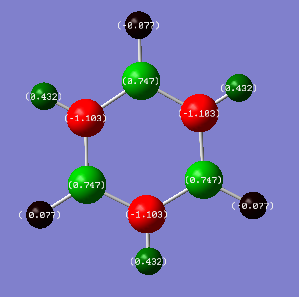Comparison: Charge analysis shows that a darker, duller colour is represented for a more neutral atom. Examining Benzene and Borazine, we can immediately see that Benzene has a lot darker colours showing that it is overall more neutral and has a more even spread of electron density compared to Borazine. In Benzene, each atom in the ring is in the same environment and so are the hydrogens. This is due to the fact that all the carbon atoms have the same electronegativity (2.55), as do the hydrogens (2.20). This leads to no net electronegativity difference between the carbons which is why there is no build up of electron on any one atom in the ring. On the other hand, the alternating Boron and Nitrogen atoms in Borazine have electronegativities 2.04 and 3.04 respectively. Nitrogen is more electronegative than boron, so it will pull electron density away from boron, deshielding its nucleus, leaving it partially positively charged. This is seen from the charge analysis, where the nitrogens are negative (-1.103) and the borons are positive (0.747). These differing electronegativities of the ring atoms cause the hydrogens to have different charges. The nitrogens are more electronegative than the hydrogens, leaving these hydrogens positively charged. The hydrogens attached to boron are almost neutral but slightly negative due to boron being very similar in electronegativity (difference = 0.17) but overall boron being more electropositive. For Benzene, all the carbon and hydrogens atoms are symmetric and results in all the charge densities being identical. For example if you rotated the benzene along its principal axis by 60 degrees, all the charges are the same. Borazine is less symmetric, therefore rotating along its principal axis by 60 degrees doesn't result in the same charge, but rotating by 120 degrees would.
Smf115 (talk) 18:07, 26 May 2018 (BST)Good charge analysis and correct colour range used across both molecules to highlight the charge distributions. To improve, try to include more terminology, for example when discussing the symmetry give mention to the point groups of the molecules or the symmetry operations themselves.
| Benzene | Borazine | MO Representations | discussion |
|---|---|---|---|
 |
 |
 |
As can be seen in the images, MO 14 and MO 15 initially look identical. However, upon closer analysis, it can be seen that in borazine, the p orbitals are slightly more displaced towards the nitrogen. This can be seen from the node gap inbetween the nitrogen being smaller than the node gap between boron. This leads to this MO in Borazine being less symmetric than the corresponding MO in Benzene. As can be seen in the MO representation column, the p orbitals point at a tangent to the ring and the lobes align in phase with the adjacent p orbitals. There are six nodes along in the MO but this is still the bonding MO as the lobes allign in phase instead of out of phase which would lead to 12 nodes. This results in this orbital only being weakly bonding for both Borazine and Benzene. This MO is also of interest as this shows that these molecules show p sigma aromaticity, which is not genrally thought of in the aromaticity argument. |
 |
 |
 |
These MOs are bonding type. For benzene, as all the carbons are identical, they all contribute p orbitals equally so for the electron lobes will be identical in size. In Borazine, boron and nitrogen don't contribute their p orobitals equally which can be seen by difference in shape of the electron lobes within the MO. |
 |
 |
 |
MO 24 for Benzene and Borazine is an antibonding MO. It comprises of the hydrogens contributing s orbitals and the p orbitals from the ring atoms. The p orbitals point towards the hydrogen atoms with opposing phase creating a node, but the other side of the p orbitals points into the center of the ring combing in phase. For Benzene, all the H s orbitals contribute equally, and all the carbon atoms contribute p orbitals equally. This leads to this MO being highly symmetric. Borazine on the other hand has varying contributions from all atoms involved. As it is the antibonding MO, the nitrogen atom now acts as the electropositive atom. This is why the electron density is pushed away from the nitrogen and builds up on their hydrogen atoms. Boron is now electronegative so draws electron density away from its hydrogens, resulting in the electron lobes on its hydrogens being much smaller. |
Smf115 (talk) 18:07, 26 May 2018 (BST)Nice range of MOs selected and a good comparison with a nice link to sigma-aromaticity for MO 14. To improve, the pi- or sigma- type identity of each of the MOs should be clearly identified but the inclusion of the LCAO diagrams is good detail.
Discussion
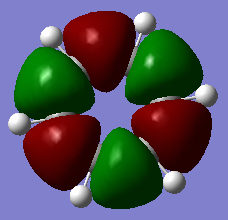
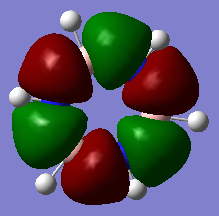
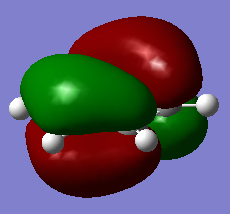
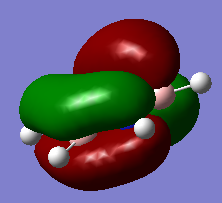
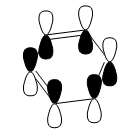
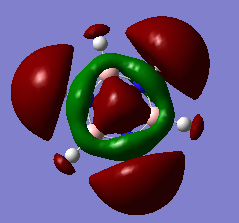
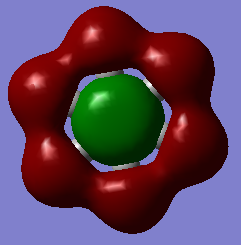
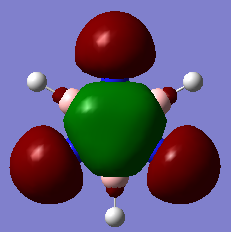
The classical picture of aromaticity is that for a molecule to be aromatic, it must be cyclic and planar, with 4n + 2 pi electrons perpendicular to the ring. This was then used to say that the pz orbitals overlap causing the electrons in these orbitals to delocalise, stabilising the ring. Whilst this is true for many cases, there is also a large group of molecules which are not planar, but still observe the stability of the cyclic ring like aromatic molecules. This allows us to broaden our concept of aromaticity to not always exclude non planar molecules. Interestingly, even benzene, which is one of the first molecules examined to have these aromatic properties, is actually non-planar at lowered temperatures, but still observes its stability.[1] Also, as explained above, aromaticity is often only thought of as the pz orbitals overlapping as pi bonds, however stabilisation of these rings can also be connected to sigma aromaticity. This case is where sigma bonds contribute to this stability of the molecule. For example, MO14 and MO15 for benzene and borazine respectively (shown above), exhibit what might be thought of as aromaticity. The lobes overlap sigma like around the ring, causing the electrons to be more delocalised around the ring. This could also contribute to the stabilisation of benzene and borazine alike.
Another example of this is MO12 for benzene. As can be seen, there is a large delocalisation of electrons in the p orbitals overlapping with the hydrogen s orbitals. This is a large overlap of orbitals which will greatly stabilise the molecule as a whole. However, MO 10 of borazine is the equivilent of MO 12 of benzene and shows much less delocalisation over the molecule.
| Benzene | Borazine |
|---|---|
 |
 |
This further suggests that aromaticity isn't just dependant on Huckel's rules and merely the overlap of pz orbitals, but that there are other factors such as the types of atom in the ring and if there are different atoms in the ring, to what extent their electronegativities effect the extent of stabilisation of the aromatic compound. To show the extent of aromaticity, the combustion of borazine could be utilised. Measure the enthalpy change and compare it to the expected energy of the 3 x B=N bond. Do the same for benzene. Then compare the energy differences found for each compound and see which one has the largest difference in energy (most stabilised).
This report into the aromaticity of Benzene and Borazine has highlighted how considering the overlapping of pz orbitals is not a good enough description of aromaticity and that Huckel's rule can not always accurately determine if a molecule is aromatic. For example, there are many MOs which also contribute to the stability of these aromatic compounds, not just the overlapping pz orbitals, but also the overlapping p orbitals in MO14 and MO15 of benzene and boarzine. There is also large indication that the symmetry of the aromatic molecule may also have effects on the stabilisation. As borazine has different atoms in the ring with different electronegativities, the distribution of electron density is much less even resulting in this reduction in symmetry and hence reduction in stabilisation.
Smf115 (talk) 18:02, 26 May 2018 (BST)Overall a good report with a well attempted project section.
References
[1]Palusiak, M. and Krygowski, T.M., 2007. Application of AIM Parameters at Ring Critical Points for Estimation of π‐Electron Delocalization in Six‐Membered Aromatic and Quasi‐Aromatic Rings. Chemistry-A European Journal, 13(28), pp.7996-8006.