Afg216MRDLab
EXERCISE 1: H + H2 system
Finding Transition States
What value do the different components of the gradient of the potential energy surface have at a minimum and at a transition structure? Briefly explain how minima and transition structures can be distinguished using the curvature of the potential energy surface.
In the situation where A is travelling towards the vibrating molecule B-C, the gradient of the surface along the minimum energy path (MEP) is positive in the A-B direction - showing the increasing potential energy (PE) as the A and B atoms converge - and zero in the B-C direction. This is characteristic of an energy minimum (zero gradient in one direction (and a positive second derivative) and not zero in the other); here, this minimum represents equilibrium bond length in the B-C molecule. Beyond the transition state maximum the gradients swap; the gradient in the A-B direction is now zero along the MEP (and the second derivative is still positive) and negative in the B-C direction, showing the decreasing PE as the C atom travels away from the newly formed A-B molecule.
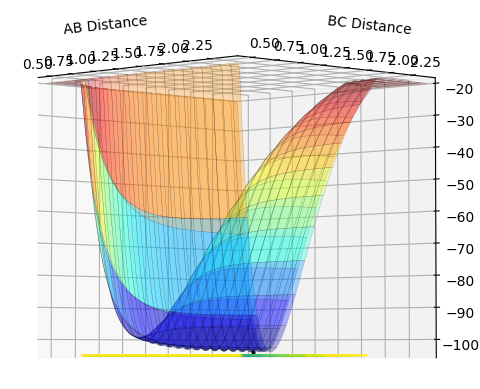
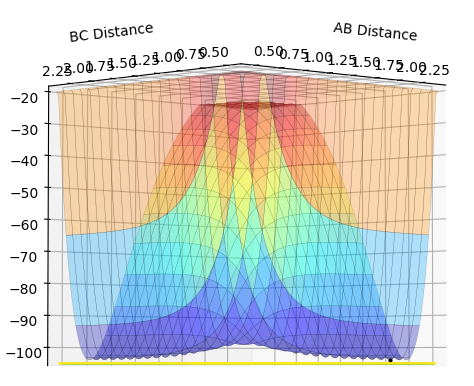
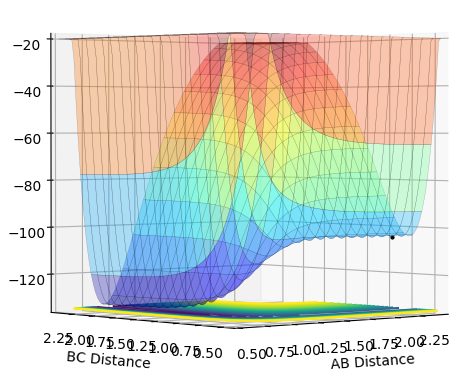
At the point representing the transition state, we have a maximum along the MEP, representing the fact that the transition state is at the PE maximum - the system experiences an overall PE decrease if the system travels back to the reactants or forward to the products. As it is a maximum in both directions, it can be seen that the gradient at that point in either direction is zero, and that the second derivative is less than zero. This point is a saddle point - along the axis where r1 + r2 is a constant, this is a PE maximum, but in the orthogonal direction, the situation where r1 = r2, this point is a PE minimum. Views along the two axes are shown below.
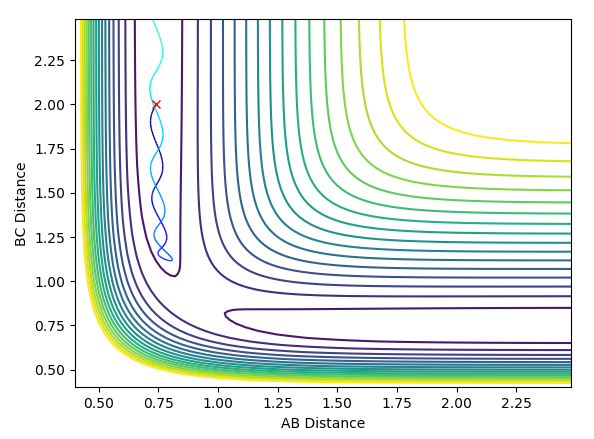
Report your best estimate of the transition state position (rts) and explain your reasoning illustrating it with a “Internuclear Distances vs Time” plot for a relevant trajectory.
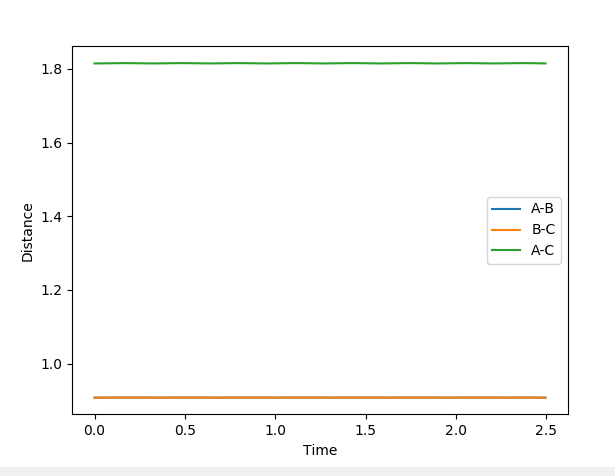
A best estimate of the transition state position is r1 = r2 = 0.9075 Å. This was found by changing the initial positions of the atoms (where r1 = r2 as the system is symmetrical across A-B and B-C) until as near to no oscillation as possible was observed. This point represents where all gradients are zero and so we have no net force (represented by the gradient of the potential surface) and no spontaneous nuclear motion. The near-constant internuclear distances against time with the starting positions of r1 = r2 = 0.9075 Å are shown below.
Finding the Minimum Energy Path (MEP) and Comparing its Calculation to that of Reaction Trajectories
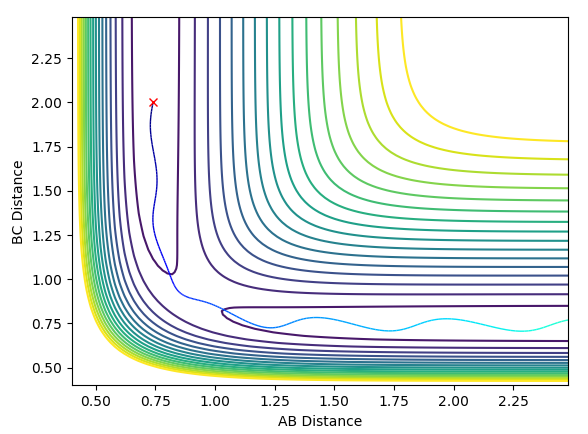
Comment on how the mep and the trajectory you just calculated differ.
The MEP represents an energy path where the velocity (and consequently the kinetic energy (KE)) is reset to zero after each time step - the overall energy of the system decreases as the system travels away from the transition state as PE is converted to KE and removed. The dynamic trajectory calculated, however, does not reset the KE to zero at each time step. Consequently, KE is gained after each time step as the particle drops down the gradient away from the transition state position and loses PE.
This increase in kinetic energy manifests itself as an oscillation in the direction of the bond (as by conservation of energy KE + PE is always constant - the oscillation of the bond increases as the kinetic energy increases and as the potential energy is lost), which can be observed in the dynamics trajectory and not in the MEP.
Take note of the final values of the positions r1(t) r2(t) and the average momenta p1(t) p2(t) at large t.
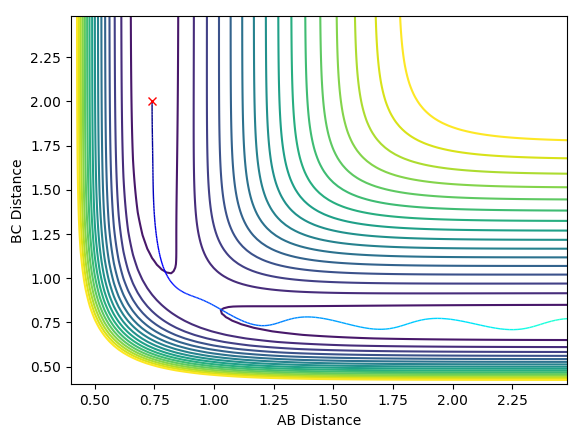
At large t the final value of r2 increases and will continue doing so as t increases; the further from the new molecule the rebounding atom travels, the less it will increase by as the change in momentum is proportional to the force exerted on the object (in that direction) and the force decreases by 1/distance2. It will increase by less and less until the force becomes negligible (as distance tends to infinity) and momentum becomes constant. For 500 time steps, we have a distance of around 8.2 at t = 2.5. The value of r1 oscillates about a constant at large t - the constant is the equilibrium bond length of the newly formed molecule. Here it is around 0.75 Å.
What would change if we used the initial conditions r1 = rts and r2 = rts + 0.01 instead?
The system will travel down the other side of the transition state and a bond will form between the other two particles to in the previous situation (e.g. between A and B where before it was B and C or vice versa).
Setup a calculation where the initial positions correspond to the final positions of the trajectory you calculated above, the same final momenta values but with their signs reversed. What do you observe?
The system rises in potential energy along the MEP with decreasing oscillation until it reaches the transition state position, at which point the system comes to rest (if it has precisely the correct energy) as all of its KE has been concerted to PE.
Testing the Reactiveness of Different Initial Conditions
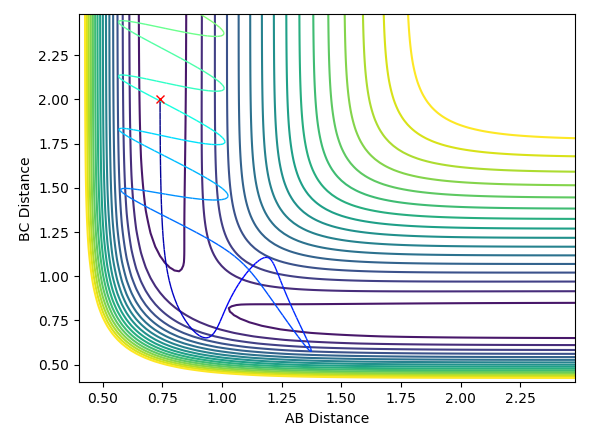
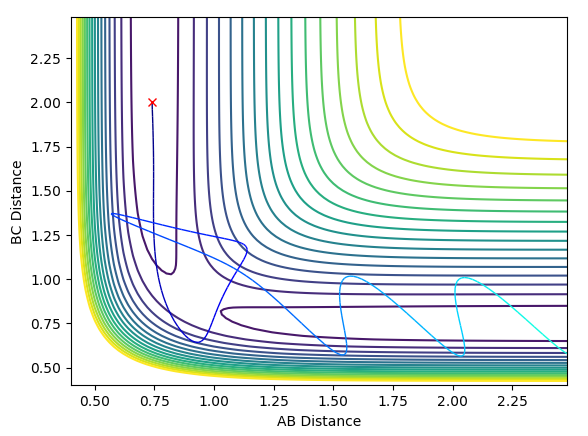
Complete the table by adding a column with the total energy, and another column reporting if the trajectory is reactive or unreactive. For each set of initial conditions, provide a plot of the trajectory and a small description for what happens along the trajectory.
Initial conditions: r1 = 0.74 Å; r2 = 2.0 Å
| Path | p1 | p2 | Total Energy (Kcal/mol) | Reactive? |
| 1 | -1.25 | -2.50 | -99.119 | Yes |
| 2 | -1.50 | -2.00 | -100.456 | No |
| 3 | -1.50 | -2.50 | -98.956 | Yes |
| 4 | -2.50 | -5.00 | -84.956 | Yes - but returns to the reactant state |
| 5 | -2.50 | -5.20 | -83.416 | Yes - but after returning to the reactant state |
| Image of Path | Description | |
| Path 1 | 
|
The system simply follows the MEP with enough energy to cross the transition state to the products. Once it has reacted vibrational energy is gained (from the conversion of PE) which it did not possess before it reacted. |
| Path 2 | 
|
The system follows the MEP towards the TS but does not possess the appropriate total energy needed to surpass it. It falls back down towards the reactants, vibrating along the way. |
| Path 3 | 
|
The system travels along the MEP towards the TS with a little vibrational energy. After overcoming the TS energy a little more of its energy is converted to vibrational energy and the product molecule oscillates with greater amplitude. |
| Path 4 | 
|
The system starts with no vibrational energy but a large amount of translational energy. It crosses over the TS but returns to the reactant state as the newly formed bond is vibrating too aggressively to stay associated. The system returns to the original reactant state with a large amount of its translational energy converted to vibrational energy - but not enough for it to return across the transition state a second time. |
| Path 5 | 
|
The system starts with no vibrational energy but much translational energy. It crosses over the TS easily but due to large amplitude oscillations and high vibrational energy it returns back to the reactants. The same happens again, and it returns to the products region where it settles, with lots of vibrational energy. |
Transition State Theory
State what are the main assumptions of Transition State Theory. Given the results you have obtained, how will Transition State Theory predictions for reaction rate values compare with experimental values?
Transition state theory assumes that the the nuclei involved behave in accordance with classical mechanics and any reaction will proceed via the lowest saddle point or transition state. In bulk scenarios (which are largely irrelevant here in our three atom situations) it assumes that the atoms in the reactant state have Boltzmann-distributed energies and that the reactants and products are both in equilibrium with the transition state - the flux through the transition state from either direction is equal.
Ng611 (talk) 13:56, 1 June 2018 (BST) This isn't entirely correct. TS theory assumes that the reactants are in equilibrium with the TS and when the TS state us crossed that product will form. Thus, if TS theory predicted equal flux through the TS, then there would be no overall reaction
Transition state theory might predict lower rates of reaction as it neglects quantum effects like tunneling, which allows a reaction to occur with less than the minimum energy it might need in a classical situation. Tunneling increases the reaction rate by providing another, lower energy pathway for reaction. Other higher energy saddle points on other reaction pathways might also affect the reaction rate.
Ng611 (talk) 13:57, 1 June 2018 (BST) What about recrossing of the transition state? This is by far the most important effect.
Exercise 2: F-H-H System
Energetics
Classify the F + H2 and H + HF reactions according to their energetics (endothermic or exothermic). How does this relate to the bond strength of the chemical species involved?
The F + H2 reaction is an exothermic process and the H + HF reaction is an endothermic process. This reflects the nature of the bonds being formed and broken in each reaction. The H-F bond is much stronger and thus when it is formed lots of energy is given off, and when it is broken a lot of energy needs to be taken in to overcome the barrier. This is represented by the different heights of the reactant and product states in each; the H-H and F situation is higher in energy (represented by height in the figure below where A is F and B and C are H) than the H-F and H situation due to the differing bond strengths discussed before.
Locate the approximate position of the transition state.
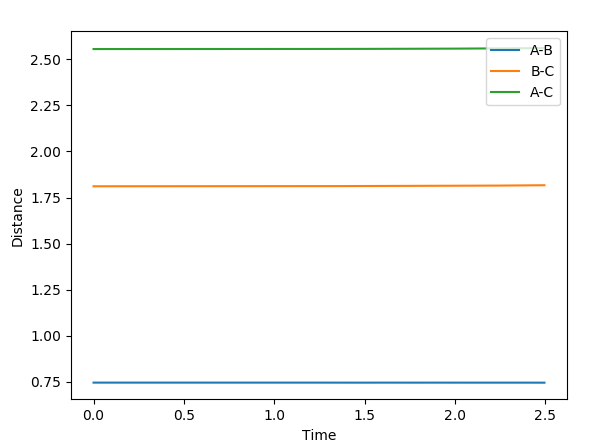
The system stays stationary when placed at approximately r1 = 0.745 Å and r2 = 1.811 Å, where r1 is the distance between the hydrogen atoms and r2 is the distance between the central hydrogen atom and the fluorine atom. The stationary nature of the system whe placed at that point is shown below.
Report the activation energy for both reactions.
Ea [General]: TS Energy - Reactant Energy
Ea [F + H2]: (-103.752) - (-104.010) = 0.258 Kcal/mol
Ea [H + HF]: (-103.752) - (-134.025) = 30.273 Kcal/mol
where the energy of the reactants in each calculation was found as the energy at the point where the state is sent far enough away into the reactant region and away from the transition state that the gradient becomes approximately zero - an approximation of infinite distance.
Ng611 (talk) 15:08, 1 June 2018 (BST) You should provide some trajectories to back these results up.
Polanyi's Rules
Identify a set of initial conditions that results in a reactive trajectory for the F + H2, and look at the “Animation” and “Internuclear Momenta vs Time”. In light of the fact that energy is conserved, discuss the mechanism of release of the reaction energy. How could this be confirmed experimentally?
The potential energy lost by the system when forming the more stable H-F bond is transformed into vibrational kinetic energy in the H-F bond in this simulation, which is then transmitted to the surroundings via collisions. In an experimental situation, this manifests itself as an increase in thermal energy - the temperature should rise.
Ng611 (talk) 15:07, 1 June 2018 (BST) True, but both translational and vibrational kinetic energy will result in a temperature increase, so calorimetry doesn't allow you to discriminate between them.
Setup a calculation starting on the side of the reactants of F + H2, at the bottom of the well rHH = 0.74, with a momentum pFH = -0.5, and explore several values of pHH in the range -3 to 3 (explore values also close to these limits). What do you observe?
The larger the vibrational energy given to the H-H molecule, the more likely it is that the molecule will cross to the product region and return to the reactants (as this vibrational energy is so great that it easily exceed the activation energy if it is transferred to translational energy appropriately).
Discuss how the distribution of energy between different modes (translation and vibration) affect the efficiency of the reaction, and how this is influenced by the position of the transition state.
Polanyi's rules state that having a larger proportion of vibrational energy than translational energy promotes later barrier (endothermic) reactions and hinders earlier barrier (exothermic) reactions, and that having a larger proportion of energy in the translational mode promotes early barrier reactions and hinders later barrier reactions.
The rules were reflected in the results of the simulations run here, where more vibrational energy in the exothermic (early barrier) F + H2 reaction was seen to more often result in an unreactive trajectory (reducing reaction efficiency). The opposite was true for the endothermic H + HF reaction, where more vibrational energy in the H-F bond in fact increased the efficiency of the reaction, even when the total momentum is larger.
Ng611 (talk) 15:07, 1 June 2018 (BST) It's not enough to say that the simulations showed that they followed Polanyi's rules -- you need to back this up with trajectories.
References
Polanyi's Rules: Theoretical Study of the Validity of the Polanyi Rules for the Late-Barrier Cl + CHD3 Reaction, Z. Zhang, Y. Zhou, and D. H. Zhang, J. Phys. Chem. Lett. 3, 23, 3416-3419
Atkins and de Paula: Physical Chemistry, 7th Edition
TS Theory: T. Bligaard, J.K. Nørskov, in Chemical Bonding at Surfaces and Interfaces, 2008; Chemical Kinetic and Dynamics, J. I. Steinfeld, J. S. Francisco, W. L. Hase, Prentice-Hall.
Ng611 (talk) 15:10, 1 June 2018 (BST) Some good parts to this report, although you really let yourself down by not providing trajectories for a lot of your final section. Remember to always include results to back up your statements!