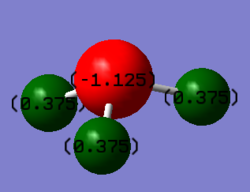
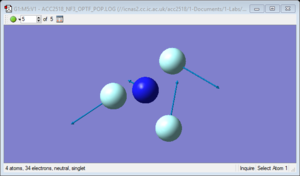
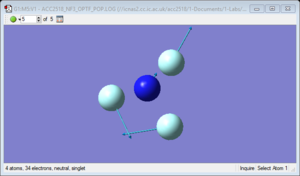
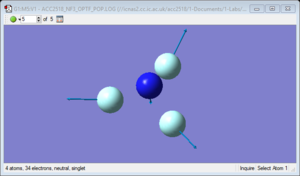
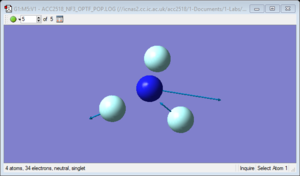
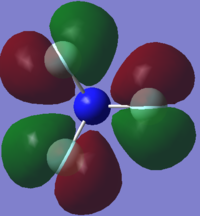
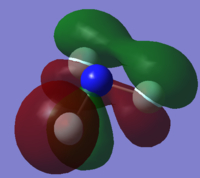
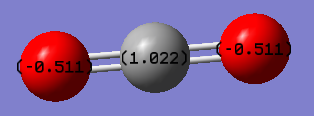
NH₃ molecule

Optimisation data

NH₃ optimisation
Calculation method	RB3LYP
Basis set	6-31G(d.p)
Final energy E(RB3LYP)	-56.55776873 (au)
RMS gradient	0.00000485 (au)
Point group	C_3V
Bond length (N-H)	1.02 (Å)
Bond angle (H-N-H)	106(°)

 Item               Value     Threshold  Converged?
 Maximum Force            0.000004     0.000450     YES
 RMS     Force            0.000004     0.000300     YES
 Maximum Displacement     0.000072     0.001800     YES
 RMS     Displacement     0.000035     0.001200     YES

NH3 molecule

Optimised NH_{3 .log file (acc2518)}

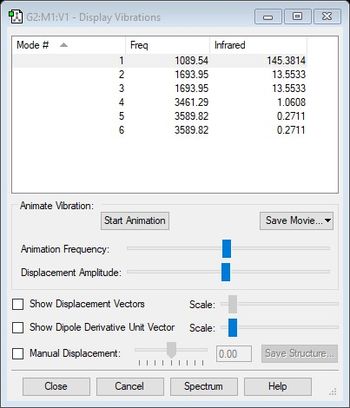
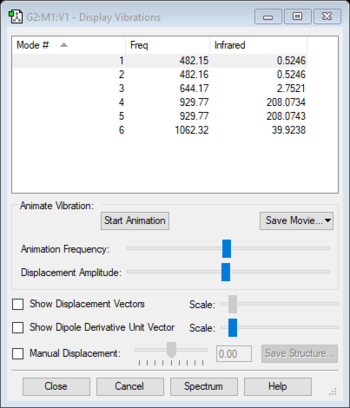
Vibrations

IR vibration data

Wavenumber (cm^-1)	1090	1694
Symmetry	A1	E
Intensity (arbitrary units)	145	14
Image
Wavenumber (cm^-1)	1694	3461
Symmetry	E	A1
Intensity (arbitrary units)	14	1
Image

Wavenumber (cm^-1)	3590	3590
Symmetry	E	E
Intensity (arbitrary units)	0	0
Image

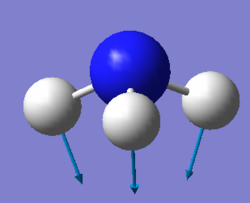
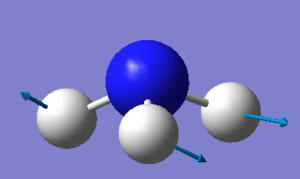
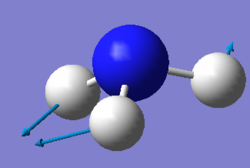
Using the 3N-6 rule, where N represents the number of atoms in a molecule, it is expected that ammonia will have six vibrational modes as shown above. There are two pairs of degenerate modes with a frequency of 1694 (cm^-1) and 3590 (cm^-1). The modes with a frequency of 1090 (cm^-1) and 1694 (cm^-1) correspond to bending vibrations and the modes with a frequency 3461 (cm^-1) and 3590 (cm^-1) correspond to bond stretch vibrations. The bond stretch vibration at 3461 (cm^-1) is highly symmetric whilst the stretches with a frequency of 3590 (cm^-1) are asymmetric. The bending vibration with a frequency of 1090 (cm^-1) is known as the umbrella mode. Three bands would be expected to be seen with the two stretches at 3590 (cm^-1) being too low in intensity. The bends with a frequency of 1694 (cm^-1) are degenerate and only one band will be observed between the two. Hence the three observed bands would be at 1090 (cm^-1), 1694 (cm^-1) and 3461 (cm^-1).

Charge analysis

Nitrogen has a greater electronegativity than hydrogen and hence there is greater electron density distributed around the N atom in ammonia relative to hydrogen. This explains the negative charge on N and the positive charge on H.

N₂ molecule

Optimisation data

N₂ optimisation
Calculation method	RB3LYP
Basis set	6-31G(d.p)
Final energy E(RB3LYP)	-109.52412868 (au)
RMS gradient	0.00000060 (au)
Point group	D_∞h
Bond length (N-N)	1.11 (Å)

         Item               Value     Threshold  Converged?
 Maximum Force            0.000001     0.000450     YES
 RMS     Force            0.000001     0.000300     YES
 Maximum Displacement     0.000000     0.001800     YES
 RMS     Displacement     0.000000     0.001200     YES

Nitrogen molecule

Optimised N₂ .log file (acc2518)

Vibrations

IR vibration data
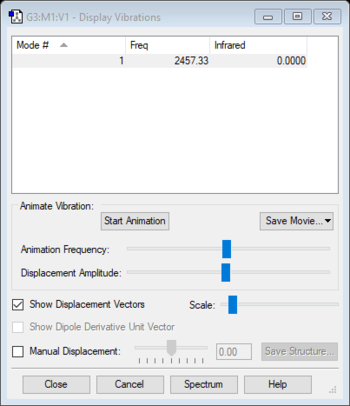
Wavenumber (cm^-1)	2457
Symmetry	SGG
Intensity (arbitrary units)	0
Image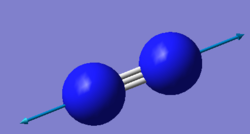

Using the 3N-5 rule for linear molecules, Nitrogen can be expected to have one vibrational mode but this mode has an IR intensity of zero since Nitrogen molecules are IR inactive. This is because they have no overall dipole.

Charge analysis

Both nitrogen atoms have the same electronegativity so the charge is neutral on both atoms.

CCDC search

Unique identifier: VAMQAE

Deposition number: 1530121

The complex linked above contains nitrogen coordinated to cobalt with a N-N bond distance of 1.08 Å which is slightly shorter than the optimised N-N bond length, displayed above, of 1.11 Å (2.d.p). During the optimisation process for nitrogen, assumptions have to be made for the computational process to be carried out. Each assumption made will increase the uncertainty in measurable quantities such as the bond length. Hence, the computationally determined bond length from the optimisation is a model and may not fully reflect the true bond length or the bond length determined by a computational program considering slightly different assumptions.

It should also be considered that the optimisation gave a prediction for the N-N bond length in a nitrogen molecule whereas the molecule linked above contains a nitrogen molecule that is coordinated into a transition metal complex. A lone pair of electrons on one of the nitrogen atoms has been donated to a cobalt ion, this draws electron density away from the donating nitrogen atom and would therefore slightly increase the positive charge on this atom. This may cause the donating nitrogen atom to attract the electrons in the N-N bond more strongly which would then explain the shorter bond in the transition metal complex compared to the nitrogen molecule.

H₂ molecule

Optimisation data

H₂ optimisation
Calculation method	RB3LYP
Basis set	6-31G(d.p)
Final energy E(RB3LYP)	-1.17853936 (au)
RMS gradient	0.00000017 (au)
Point group	D_∞h
Bond length (H-H)	0.74 (Å)

 Item                     Value        Threshold  Converged?
 Maximum Force            0.000000     0.000450     YES
 RMS     Force            0.000000     0.000300     YES
 Maximum Displacement     0.000000     0.001800     YES
 RMS     Displacement     0.000001     0.001200     YES

Hydrogen molecule

Optimised H₂ .log file (acc2518)

Vibrations

IR vibration data
Wavenumber (cm^-1)	4466
Symmetry	SGG
Intensity (arbitrary units)	0
Image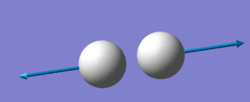

Using the 3N-5 rule for linear molecules, hydrogen can be expected to have one vibrational mode but this mode has an IR intensity of zero since hydrogen molecules, like nitrogen molecules, are IR inactive.

Charge analysis

Both hydrogen atoms have the same electronegativity so the charge is neutral on both atoms.

The Haber-Bosch process

N₂ + 3H₂ -> 2NH₃

E(NH3)=-56.55776873

2*E(NH3) =2*(-56.55776873)=-113.11553746

E(N2) =-109.52412868

E(H2)=-1.17853936

3*E(H2) =3*(-1.17853936) =-3.53561808

ΔE= 2*E(NH3) -[ E(N2) + 3*E(H2) ]= -0.05579069 ≈ -0.05579 au (5.d.p)

ΔE=-146.5 kJ/mol (1.d.p)

ΔE is negative which indicates that the gaseous reactants are less stable than the ammonia product since the reactants are at a higher energy than the product. Although this process is not necessarily entropically favourable with four reactant gaseous molecules forming two gaseous product molecules, the reaction has a significantly negative enthalpy change which reflects the result calculated above.

Project molecule (NF₃)

Optimisation data

NF₃ optimisation
Calculation method	RB3LYP
Basis set	6-31G(d.p)
Final energy E(RB3LYP)	-354.07131058 (au)
RMS gradient	0.00010256 (au)
Point group	C_3V
Bond length (N-F)	1.38 (Å)
Bond angle (F-N-F)	102(°)

 Item                     Value       Threshold  Converged?
 Maximum Force            0.000164     0.000450     YES
 RMS     Force            0.000108     0.000300     YES
 Maximum Displacement     0.000612     0.001800     YES
 RMS     Displacement     0.000296     0.001200     YES

NF3 molecule

Optimised NF_{3 .log file (acc2518)}

Vibrations

IR vibration data

Wavenumber (cm^-1)	482	482
Symmetry	E	E
Intensity (arbitrary units)	1	1
Image
Wavenumber (cm^-1)	644	930
Symmetry	A1	E
Intensity (arbitrary units)	3	208
Image

Wavenumber (cm^-1)	930	1062
Symmetry	E	A1
Intensity (arbitrary units)	208	40
Image

Nitrogen trifluoride has the same number of atoms as ammonia and so six vibrational modes can be predicted from the 3N-6 rule. There are also two pairs of degenerate modes with frequencies of 482 (cm^-1) and 930 (cm^-1). The modes with a frequency of 482 (cm^-1) and 644(cm^-1) correspond to bending vibrational modes and the modes with a frequency of 930 (cm^-1) and 1062 (cm^-1) correspond to stretching vibrational modes. The mode with a frequency of 1062 (cm^-1) represents a symmetric stretch whilst the modes with a frequency of 930 (cm^-1) represent asymmetric stretches. In contrast to ammonia, the highest frequency bond stretch of nitrogen trifluoride is the symmetric stretch.

Three bands can be expected in the NF₃ IR spectrum at frequencies of 644 (cm^-1) 930 (cm^-1) and 1062 (cm^-1). The bends at 482 (cm^-1) will be too low in frequency to appear in the spectrum which starts at a frequency of 500 (cm^-1). The stretches at 930 (cm^-1) are degenerate and hence will only display one band between them. The band as 644 (cm^-1) may not be clearly visible due its relative low intensity of 3 arbitrary units.

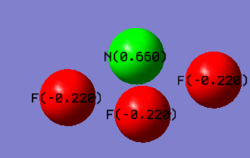
Charge analysis

Fluorine has a greater electronegativity that nitrogen and therefore there is greater electron density distributed around the three fluorine atoms compared to the nitrogen atom. The three fluorine atoms are treated as equivalent which means that the magnitude of the positive charge on nitrogen is three times the magnitude of the negative charge on a single fluorine atom.

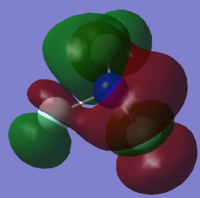
Molecular orbitals (MO)

The nitrogen atom contributes 7 electrons and each fluorine atom contributes 9 electrons which means that nitrogen trifluoride contains 34 electrons in total and hence 17 electron pairs. In the table below, a molecular orbital number of 1 would denote the molecular orbital that is deepest in energy. Therefore, orbital 17 represents the HOMO and orbital 18 represents the LUMO. All of the molecular orbitals shown below are occupied with the exception of the LUMO.

Molecular orbital number	Type of molecular orbital	Energy (au)	Extra details
18	Antibonding	0.01947	There are nodes in the centre of the N-F bonds which indicates that the LUMO is an antibonding orbital with destructive inteference between phases of opposite sign. The nodes in the centre of all four atoms also indicate that this MO was formed from 2p atomic orbitals from both nitrogen and fluorine.
17	Bonding	-0.35162	The phase denoted by the green region shows orbital overlap across all three N-H bonds which implies that the HOMO is a bonding orbital. This MO has been formed from 2p orbitals which explains the nodes observed in the centre of the F atoms.
16	Non-bonding	-0.42224	There is no electron density along any of the bonds which is the key indicator that this is a non-bonding MO. Since the electron density is localised around the fluorine atoms, this MO appears to show lone electron pairs on these fluorine atoms. There is no electron density being shared between the fluorine atoms which suggests there is destructive interference preventing such an interaction.
15	Bonding	-0.43590	As observed in the HOMO, there is electron density along all three bonds which indicates the bonding nature of the MO. However, in contrast to the HOMO, the electron density along the bonds is not in the same phase for each bond. There is also some constructive interference between two of the F atoms which appears to indicate a very partial π character between the two atoms. This also means that this interaction is the product of two 2p atomic orbitals on fluorine overlapping slightly in phase with each other.
5	Bonding	-1.35870	This MO contains no nodes at all implying that it is bonding in nature. It is also formed from overlap of 2s orbitals, in phase, on all atoms since the entire molecule is encased in electron density as a result of the constructive interference. It cannot be formed from 1s orbitals which would be far lower in energy and will also only occupy the first 4 MOs since there are 8 1s electrons in NF₃.

Bonus Molecule (CO₂)

Optimisation data

CO₂ optimisation
Calculation method	RB3LYP
Basis set	6-31G(d.p)
Final energy E(RB3LYP)	-188.58093945 (au)
RMS gradient	0.00001154 (au)
Point group	D_∞h
Bond length (C-O)	1.17 (Å)
Bond angle (C-O-C)	180 (°)

 Item                     Value        Threshold  Converged?
 Maximum Force            0.000024     0.000450     YES
 RMS     Force            0.000017     0.000300     YES
 Maximum Displacement     0.000021     0.001800     YES
 RMS     Displacement     0.000015     0.001200     YES

Carbon dioxide molecule

Optimised CO₂ .log file (acc2518)

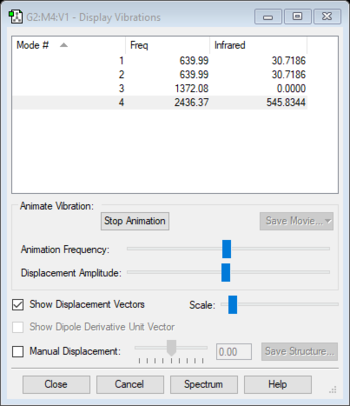
Vibrations

IR vibration data

Wavenumber (cm^-1)	640	640
Symmetry	PIU	PIU
Intensity (arbitrary units)	31	31
Image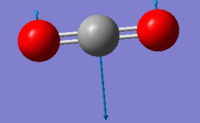
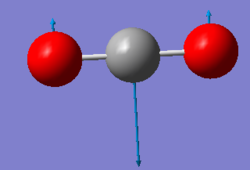
Wavenumber (cm^-1)	1372	2436
Symmetry	SGG	SGU
Intensity (arbitrary units)	0	546
Image

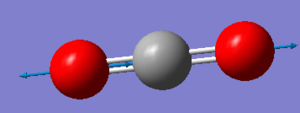
Using the 3N-5 rule for linear molecules, carbon dioxide can be expected to have 4 vibrational modes. The modes with a frequency of 640 cm^-1 correspond to bends and the modes with frequencies of 1372 cm^-1 and 2436 cm^-1 correspond to stretches. The two modes with a frequency of 640 cm^-1 are degenerate and will only produce one IR band between them. The stretch with a frequency of 1372 will not produce an IR band as the stretch is symmetric and has no overall dipole. The asymmetric stretch at 2436 cm^-1 will also produce an IR band to give two IR bands overall.

Charge analysis

Oxygen has a greater electronegativity than carbon which explains the negative charge on each oxygen atom and the positive charge on the central carbon atom.

Marking

Note: All grades and comments are provisional and subject to change until your grades are officially returned via blackboard. Please do not contact anyone about anything to do with the marking of this lab until you have received your grade from blackboard.

Wiki structure and presentation 1/1

Is your wiki page clear and easy to follow, with consistent formatting?

YES

Do you effectively use tables, figures and subheadings to communicate your work?

YES

NH3 1/1

Have you completed the calculation and given a link to the file?

YES

Have you included summary and item tables in your wiki?

YES

Have you included a 3d jmol file or an image of the finished structure?

YES

Have you included the bond lengths and angles asked for?

YES

Have you included the “display vibrations” table?

YES

Have you added a table to your wiki listing the wavenumber and intensity of each vibration?

YES

Did you do the optional extra of adding images of the vibrations?

YES

Have you included answers to the questions about vibrations and charges in the lab script?

YES

N2 and H2 0.5/0.5

Have you completed the calculations and included all relevant information? (summary, item table, structural information, jmol image, vibrations and charges)

YES

Crystal structure comparison 0.5/0.5

Have you included a link to a structure from the CCDC that includes a coordinated N2 or H2 molecule?

YES

Have you compared your optimised bond distance to the crystal structure bond distance?

YES

Haber-Bosch reaction energy calculation 1/1

Have you correctly calculated the energies asked for? ΔE=2*E(NH3)-[E(N2)+3*E(H2)]

YES

Have you reported your answers to the correct number of decimal places?

YES

Do your energies have the correct +/- sign?

YES

Have you answered the question, Identify which is more stable the gaseous reactants or the ammonia product?

YES

Your choice of small molecule 4.5/5

Have you completed the calculation and included all relevant information?

YES

Have you added information about MOs and charges on atoms?

YES, overall a very good wiki with detailed explanations and a nice layout, well done! The explanation of the charges is good and most of the MO discussion is good. In MO17 however the main contribution to the N atom is of s rather than p character. Overall this MO is antibonding between the F and N atoms with pi bonding amongst the F atoms.

Independence 1/1

If you have finished everything else and have spare time in the lab you could: Check one of your results against the literature, or Do an extra calculation on another small molecule, or

You calculated CO2 well done!

Do some deeper analysis on your results so far

NH3 molecule

Optimisation data

Vibrations

Charge analysis

N2 molecule

Optimisation data

Vibrations

Charge analysis

CCDC search

H2 molecule

Optimisation data

Vibrations

Charge analysis

The Haber-Bosch process

Project molecule (NF3)

Optimisation data

Vibrations

Charge analysis

Molecular orbitals (MO)

Bonus Molecule (CO2)

Optimisation data

Vibrations

Charge analysis

Marking

Wiki structure and presentation 1/1

NH3 1/1

N2 and H2 0.5/0.5

Crystal structure comparison 0.5/0.5

Haber-Bosch reaction energy calculation 1/1

Your choice of small molecule 4.5/5

Independence 1/1

NH₃ molecule

N₂ molecule

H₂ molecule

Project molecule (NF₃)

Bonus Molecule (CO₂)