Ac4515

Exercise 1 H + H2 system

Dynamics from the transition state region

Gradient and curvature of the potential energy surface .

When the gradient of the potential surface is zero, the transition state is at an energy maximum. This scenario is known as the saddle point. At the saddle point the first derivative of potential energy surface is zero.

(The first sentence is not true. A 0 gradient on the PES is just a stationary point. A TS is a particular type of stationary point on a multidimensional PES Tam10 (talk) 14:00, 1 June 2017 (BST))

The energy minima and the transition structures can be distinguished by taking the second derivative of the potential energy surface. The minima is observed when the second derivative is greater than zero and conversely the transition structure when the second derivative is less than zero.

(This is still only in one coordinate Tam10 (talk) 14:00, 1 June 2017 (BST))

Transition state distance (r_ts)

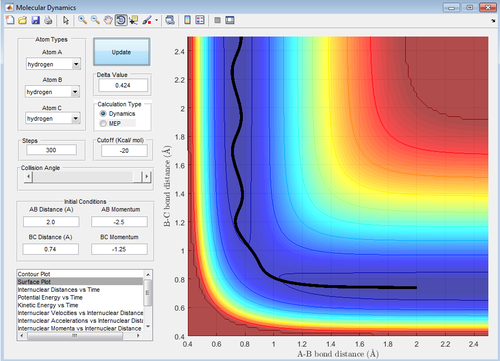
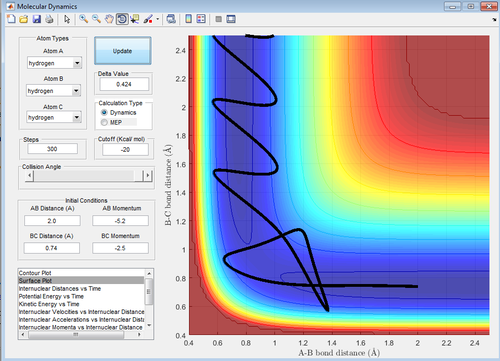
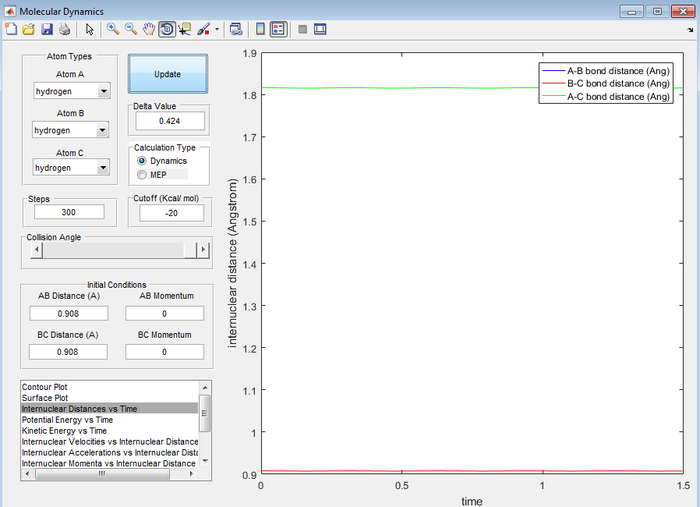
The transition state position (r_ts) was found to be at 0.908 Å. This was found by estimating from the surface plot which equal distance of r1 and r2 correspond to the saddle point and therefore the transition state. The value obtained was then confirmed by plotting a internuclear distance vs time plot (figure 1), showing no vibration thus implying a stationary transition state.

Figure 1: Internuclear distance versus Time plot for a H + H2 system.

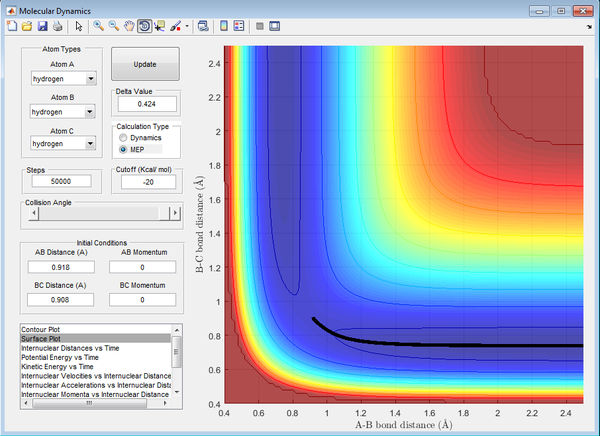
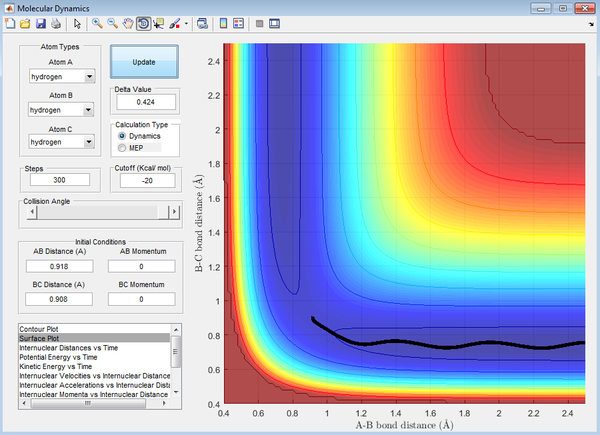
Calculating the reaction path

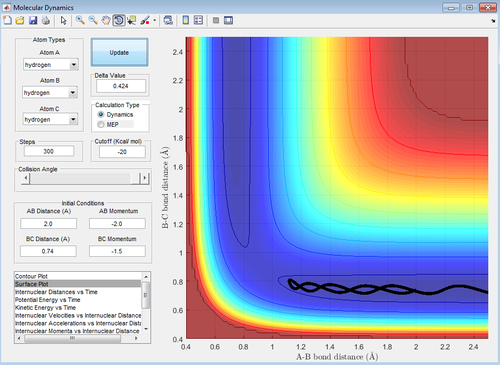
For the mep calculation, at each step the velocity is zero and thus gives a trajectory that follows the floor of the potential well (the MEP) with no vibrational energy, thus giving a linear reaction coordinate. The dynamic calculation accounts for kinetic energy of the molecule and thus gives a reaction coordinate depicting a vibrating molecule.

Figure 2: Surface plot of a MEP calculation of H+H2 system	Figure 3: Surface plot of a dynamics calculation of H+H2 system

Reactive and unreactive trajectories

Table 1

p1	p2	reactive/unreactive	Trajectory	Description
-1.25	-2.5	reactive		Hydrogen A approaches the non-vibrating BC molecule with the appropriate energy to overcome the activation energy of the transition state and form the vibrating AB molecule. The AB bond distance is constant after the transition state which is suggestive that the AB molecule has formed.
-1.5	-2.0	unreactive		Hydrogen A approaches the vibrating BC molecule with an insufficient amount of kinetic energy to overcome the activation energy that would form the product AB molecule. Therefore the reaction trajectory goes back in the direction of the reactants.
-1.5	-2.5	reactive		Contrarily to the scenario above, hydrogen A, when approaching molecule BC, now has sufficient kinetic energy (increased momentum) to overcome the activation barrier to form the vibrating molecule AB.
-2.5	-5.0	unreactive		Hydrogen A approaches the strongly vibrating BC molecule with an excess amount of kinetic energy to overcome the transition state, thus an AB molecule forms. Since the AB molecule has a large amount of vibrational energy, the reaction trajectory is able to go back across the transition state and again form a reactant BC molecule; making this an unreactive trajectory.
-2.5	-5.2	reactive		Hydrogen A approaches the non-vibrating BC molecule with a large amount of kinetic energy. The AB molecule is subsequently formed. Due to the large amount of vibrational energy of AB, the reaction trajectory is able to go back through the transition state to again form the BC molecule. However, hydrogen A has large enough amount of kinetic energy to again collide with the BC molecule and overcome the activation barrier, thus forming a AB molecule.

Assumptions of Transition state theory

There are four transition state theory assumptions .

1: Once the transition state has been reached, the products must be formed.

2: During the reaction the Boltzmann distribution is preserved for the reactant molecules.

3: Transition state complexes crossing the the critical surface from the reactant side have a Boltzmann distribution of energy corresponding to the temperature of the reacting system

4: Motion along the reaction coordinate can be treated classically. This assumption doesn't account for quantum tunneling which could potentially be occurring.

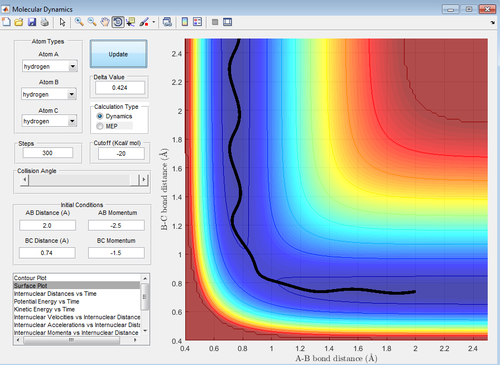
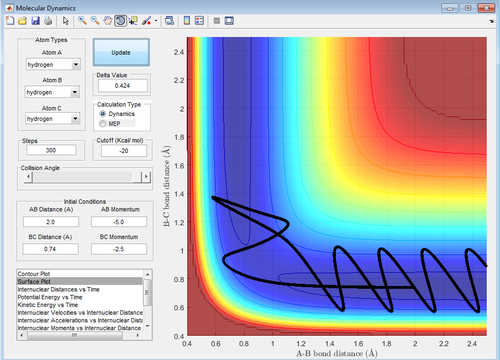
With respect to the first assumption the first three set of momenta agree with it. Conversely, the last two set of momenta is not consistent with the assumption. In both instances the transition state is reached and crossed towards the product, but, then the trajectory subsequently recrosses the transition state back to the reactant.

Exercise 2 F - H - H system

Energetics of the forward and backward reaction

Figure 4 below shows the system follows an exothermic reaction trajectory. The energy of the product is lower than the reactant. It follows that the H-F bond is stronger than a H-H bond, more energy is released when forming the H-F bond than energy put in to break the H-H bond.

If the forward reaction of H2 + F --> HF + H is exothermic, it follows that the backward reaction must be endothermic.

Figure 4: Surface plot F +H2 system

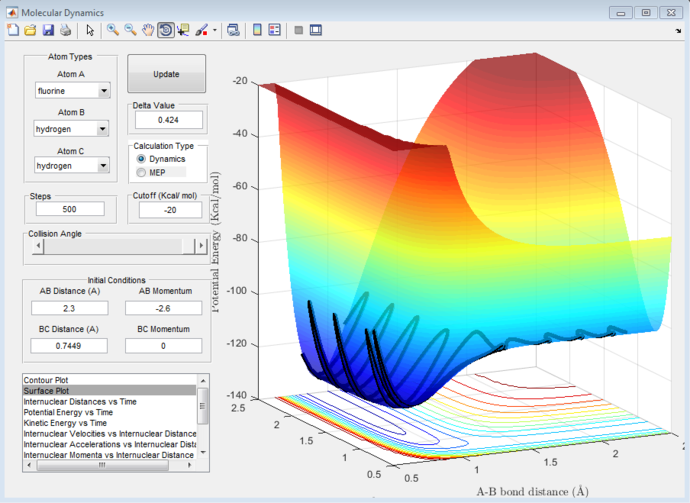
Transition state distance

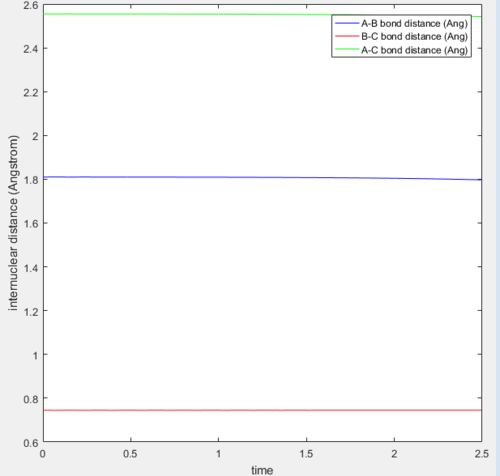
Applying Hammond's postulate to this reaction, the transition state should resemble the reactants more then the products as this reaction is exothermic. Therefore the position of transition state should be shifted towards the reactants. This is the case and is shown below in figure 5. This is also confirmed with figure 6, at the transition state the bonds have no vibrational energy

The transitions state distances were found to be 1.81 Å H-F and 0.745 Å H-H.

Figure 5: Surface plot of F + H2 system	Figure 6: Intermolecular distance vs time plot

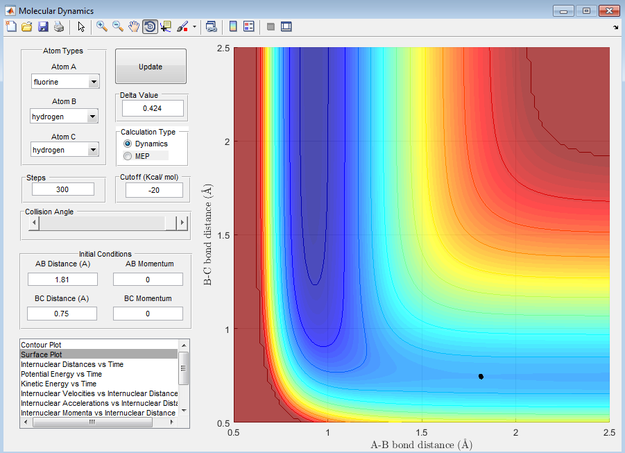Exothermic reaction- activation energy

The figure below shows the potential energy vs time graph from an mep calculation. The mep calculation was done to find the lowest energy of the reactant. To optimize the mep trajectory, sequential displacement of the reactant bonds were run until the coordinate reached the minimum energy for the reactants.

Activation energy= Transition state energy - reactant energy:

-103.75 kcal/mol - (-104.015 kcal/mol)= 0.265 kcal/mol

Figure 7: Potential energy vs Time plot

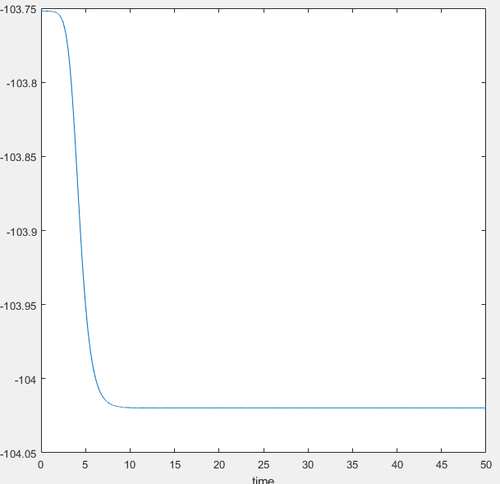
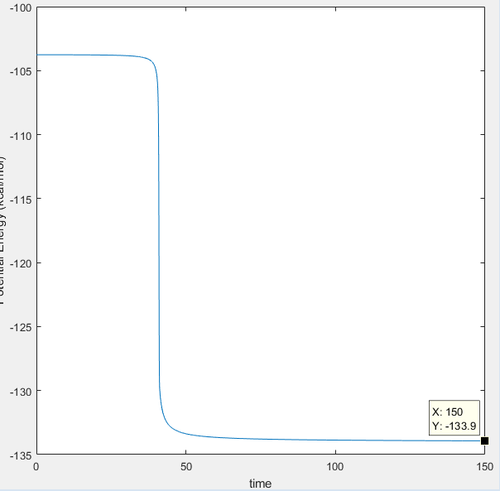
Endothermic reaction- activation energy

The same mep procedure was done for the endothermic reaction. The calculation is below.

Activation energy= Transition state energy - reactant energy:

-103.75 kcal/mol - (-133.90 kcal/mol)= 30.15 kcal/mol

Figure 8: Potential energy vs Time plot for endothermic reaction

Reaction dynamics

Release of energy mechanism

The law of conservation energy states that energy cannot be created or destroyed. As F approaches the non-vibrating H2 molecule with kinetic energy, the repulsive interaction increases the potential energy (converted from kinetic energy) of the system until it reaches the maximum potential energy, the transition state. At the transition state, all atoms in the system are stationary and all energy is potential, with no kinetic. As the system passes through the transition state towards the products, potential energy is converted into vibrational energy (in the form of the vibrating product molecule) and transnational energy (in the form of the leaving H atom).

(No, kinetic energy is required to cross the TS. Tam10 (talk) 14:00, 1 June 2017 (BST))

To confirm this experimentally, techniques such as calorimetry can be used to measure the amount heat released and gained by the system. Monitoring the vibrational energy of the system could be done with IR spectroscopy. Peaks on the IR spectrum are associated with a frequency,v, and can be related to their vibrational energy using E=hv. Therefore, one can gain the vibrational energies of the reactants and products, thus quantifying the amount of vibrational energy being converted into other forms of energy.

(This will not allow the quantification of vibrational energy, as typical IR spectroscopy involves vibrational excitation from an external source Tam10 (talk) 14:00, 1 June 2017 (BST))

Attractive and repulsive surfaces

Translational energy of the reactants is most effective at inducing reactions with an attractive surface (exothermic reactions), while a reactant molecule with vibrational energy is more effective for reactions with a repulsive surface (endothermic reactions). Following the transition state of an exothermic reaction, the translational energy is converted into vibrational energy (oscillating HF). The opposite is true for the endothermic reaction, the vibrational energy of the reactant is converted into translational energy in the diatomic product .

(You've missed a few questions here, and have given no examples for Polanyi's rules Tam10 (talk) 14:00, 1 June 2017 (BST))