ASR1234
Molecular Modelling II Bence Dallos 01335654
NH3 Molecule
Bond distance: 1.01798 Å
H-N-H bond angle: 105.741°
Calculation method: B3LYP
Basis set: 6-31G(d,p)
Final energy: -56.5577687299 a.u.
RMS Gradient: 0.0000048 a.u.
Point Group: C3v
Optimisation Table:
Item Value Threshold Converged?
Maximum Force 0.000004 0.000450 YES
RMS Force 0.000004 0.000300 YES
Maximum Displacement 0.000072 0.001800 YES
RMS Displacement 0.000035 0.001200 YES
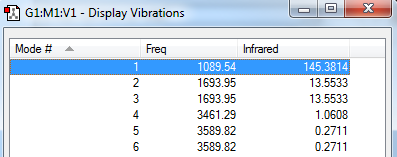
Vibrational Modes:
How many modes do you expect from the 3N-6 rule? 6
Which modes are degenerate (ie have the same energy)? The second and the third modes and the fifth and sixth ones.
Which modes are "bending" vibrations and which are "bond stretch" vibrations?1,2,3 are bends and 4,5 and 6 are vibrations.
Which mode is highly symmetric? The fourth mode.
One mode is known as the "umbrella" mode, which one is this? The first one.
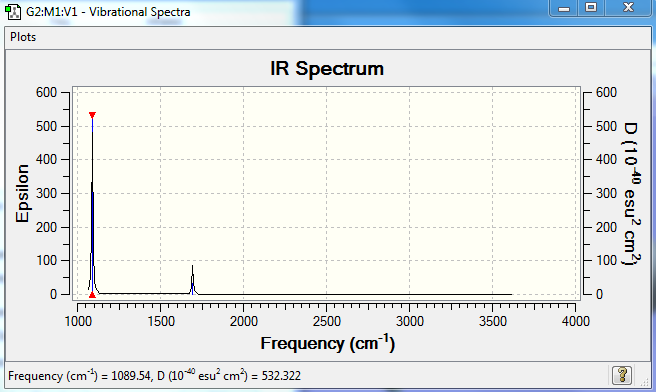
How many bands would you expect to see in an experimental spectrum of gaseous ammonia? I would expect to see two peaks on the spectrum.The most intense vibration would be the first one.Vibrations 2 and 3 would appear as a single peak due to these modes being degenerate.The 4th,5th and 6th modes are negligible due to the noise that would appear in the experimental results.
Predicted IR Spectra to confirm this:
JMol Diagram:
NH3 Molecule |
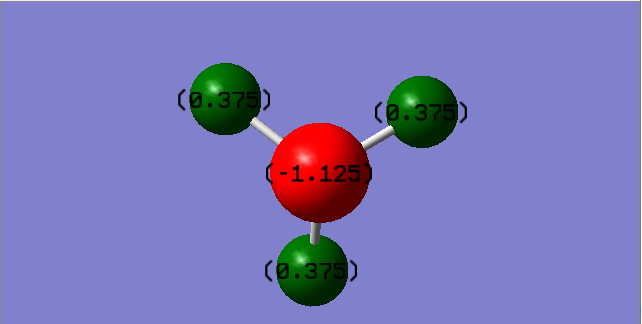
Charge Distribution of NH3:
Charge on the Nitrogen atom: -1.125
Charge on Hydrogen atom: 0.375
Nitrogen is the more electronegative atom,it withdraws electron density towards itself and hence it has a negative charge and the H atoms a small positive charge.
N2 Molecule
Bond distance: 1.10550 Å
N-N bond angle: 180 °
Calculation method: B3LYP
Basis set: 6-31G(d,p)
Final energy: -109.52412868 a.u.
RMS Gradient: 0.00000060 a.u.
Point Group: D∞h
Optimisation Table:
Item Value Threshold Converged?
Maximum Force 0.000001 0.000450 YES
RMS Force 0.000001 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000000 0.001200 YES
Vibrational Modes:
JMol Diagram:
N2 Molecule |
Charge distribution on N2:
No charge on atoms,as N2 is diatomic.
H2 Molecule
Bond distance: 0.74279 Å
H-H bond angle: 180 °
Calculation method: B3LYP
Basis set: 6-31G(d,p)
Final energy: -1.17853936 a.u.
RMS Gradient: 0.00000017 a.u.
Point Group: D*H
Optimisation Table:
Item Value Threshold Converged? Maximum Force 0.000000 0.000450 YES RMS Force 0.000000 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000001 0.001200 YES
Vibrational Modes:
JMol Diagram:
H2 Molecule |
Charge distribution on H2:
No charge on atoms,as H2 is diatomic.
Reaction Energy Calculations
E(NH3)= -56.5577687299 a.u.
2*E(NH3)= -113.1155374598 a.u.
E(N2)= -109.52412868 a.u.
E(H2)= -1.17853936 a.u.
3*E(H2)= -3.53561808 a.u.
ΔE=2*E(NH3)-[E(N2)+3*E(H2)]= -113.1155374598 a.u.- (-109.52412868 a.u.+3(-1.17853936 a.u.)=-0.0557906998 a.u. =-146.47849348304 kJ/mol
Total energy change for the reaction:-146.48 kJ/mol [1]
O2 Molecule
Bond distance: 1.21602 Å
O-O bond angle: 180°
Calculation method: B3LYP
Basis set: 6-31G(d,p)
Final energy: -150.25742434 a.u.
RMS Gradient: 0.00007502 a.u.
Point Group: D*H
Optimisation Table:
Item Value Threshold Converged? Maximum Force 0.000024 0.000450 YES RMS Force 0.000024 0.000300 YES Maximum Displacement 0.000014 0.001800 YES RMS Displacement 0.000021 0.001200 YES
Vibrational Modes:
JMol Diagram:
O2 Molecule |
Charge distribution on O2:
No charge on atoms,as 02 is diatomic.
Molecular Orbital analysis of O2
3σg bonding orbital [2]
- Energy:-0.53151 a.u.
- Combination of two pz atomic orbitals
- Bonding mixture,in gerade orientation
- Occupied molecular orbital
2σ*u antibonding orbital
- Energy:-0.79821 a.u.
- Combination of two 2s atomic orbitals
- Antibonding mixture,in ungerade orientation
- Occupied molecular orbital
2σg bonding orbital
- Energy:-1.27663 a.u.
- Combination of two 2s atomic orbitals
- Bonding mixture,in gerade orientation
- Occupied molecular orbital
σ*u antibonding orbital
- Energy:-19.30712 a.u. (deep in energy)
- Combination of two 1s atomic orbitals
- Antibonding mixture,in ungerade orientation
- Occupied molecular orbital
σg bonding orbital
- Energy:-19.30736 a.u. (deep in energy)
- Combination of two 1s atomic orbitals
- Bonding mixture,in gerade orientation
- Occupied molecular orbital
CF4 Molecule
Bond distance: 1.32939 Å [3]
C-F bond angle: 109.47122 °
Calculation method: B3LYP
Basis set: 6-31G(d,p)
Final energy: -437.47627267 a.u.
RMS Gradient: 0.00004048 a.u.
Point Group: TD
Optimisation Table:
Item Value Threshold Converged? Maximum Force 0.000078 0.000450 YES RMS Force 0.000042 0.000300 YES Maximum Displacement 0.000133 0.001800 YES RMS Displacement 0.000071 0.001200 YES
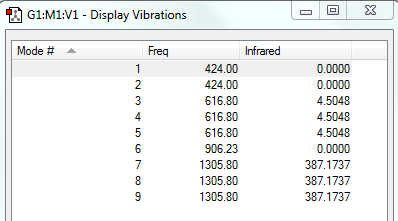
Vibrational Modes:
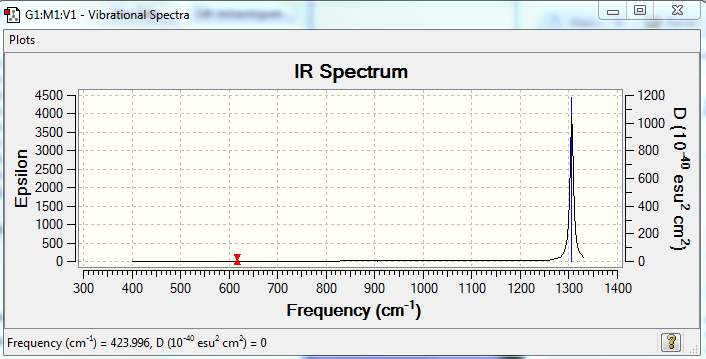
Would expect to see two peaks in the experimental spectrum.Modes 1,2 and 6 can be ignored due to the noise that would appear in the spectra. Modes 3,4 and 5 would be degenerate,appearing as one peak. In addition modes 7,8 and 9 would also be degenerate and would appear as a single peak.[4]
Predicted IR Spectra to confirm this:
JMol Diagram:
CF4 Molecule |
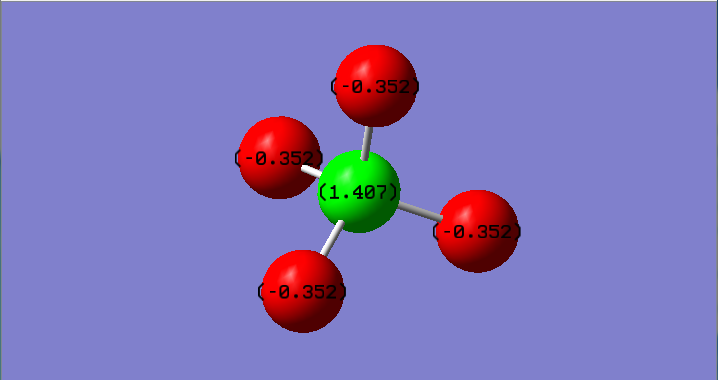
Charge Distribution of CF4:
Charge on the Carbon atom: 1.407
Charge on Fluorine atom:-0.352
Fluorine is more electronegative than carbon,therefore draws electron density towards itself, making the Fluorine negatively charged and the Carbon positively charged.
Example of a CF4 Molecular Orbital Diagram:
References
The Born-Haber Process[1] Molecular Orbital Theory[2] C-F Bond Length[3] IR Spectroscopy[4]
- ↑ 1.0 1.1 https://chem.libretexts.org/Core/Inorganic_Chemistry/Crystal_Lattices/Thermodynamics_of_Lattices/Lattice_Energy%3A_The_Born-Haber_cycle
- ↑ 2.0 2.1 http://chemed.chem.purdue.edu/genchem/topicreview/bp/ch8/mo.php
- ↑ 3.0 3.1 https://en.wikipedia.org/wiki/Carbon%E2%80%93fluorine_bond
- ↑ 4.0 4.1 https://www2.chemistry.msu.edu/faculty/reusch/VirtTxtJml/Spectrpy/Infrared/infrared.htm