AS61151
Molecular Reaction Dynamics
H + H2 system
Total gradient of the potential energy surface at a minimum and at a transition structure
The value of the total potential energy gradient at the minimum and transition state is zero, as these are turning points of the potential energy surface. The unstable transition state is a saddle point (which corresponds to the maximum point on the minimum energy pathway of the reaction), and the minimum points on the potential energy curve represent the stable reactants and products. The minimum and maximum can be distinguished by the curvature (representative of the second derivative) of the potential energy surface plot. The value of the second derivative will be negative at the maximum points and positive at minimum. For the transition structure two possible outcomes are possible as a result of minor displacement either it rolls towards the products or reactants, whereas for the minimum slight displacement will eventually eventually return to the same minimum point on the potential energy surface.
Estimate of the transition state position
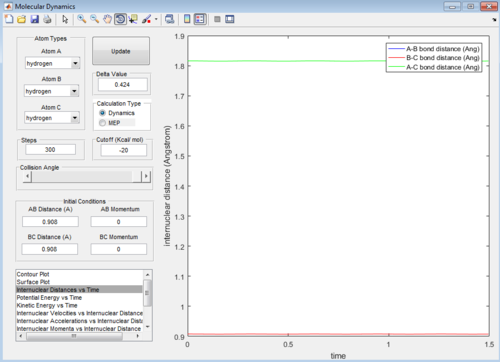
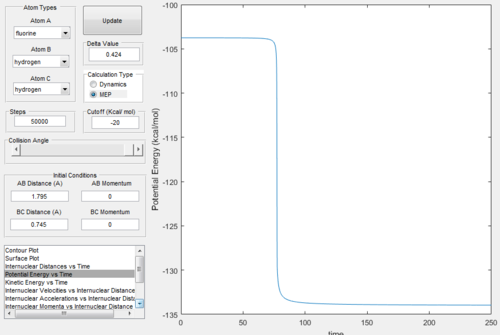
The inter-nuclear between the hydrogen atoms at the transition state, Rts = 0.908 Å As this internculear distance remains constant with time, when the initial momenta is zero, which means at this position lies on the saddle point in the potential energy surface plot, so corresponds to the transition state position.
Minimum Energy Path (mep) and Dynamics calculations
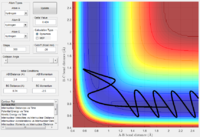
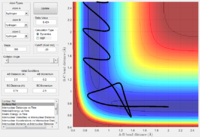
The trajectory from the mep calculation follows a well-defined path (the valley floor), whilst the trajectory from the dynamics calculation oscillates with time.
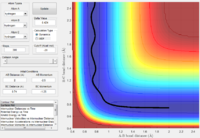
Reactivity of trajectories from different initial momenta
| p1 | p2 | Result | Screenshot | Description |
|---|---|---|---|---|
| -1.25 | -2.5 | Reactive |  |
The reactants (H and H2) have sufficient energy to overcome the activation barrier and hence pass through the transition state and subsequently are converted to the products. |
| -1.5 | -2.0 | Unreactive |  |
The reactants have insufficient energy to overcome the activation barrier, thus the trajectory is that the reactants approach the entrance channel (transition state) but cannot pass through so instead bounce back to the reactants. |
| -1.5 | -2.5 | Reactive |  |
The reactants have sufficient energy to overcome activation energy so reaction occurs and products form. |
| -2.5 | -5.0 | Unreactive |  |
Due to the relatively high momentum (p2) of the incoming Hydrogen atom, the reactants have very high energy enough to go past the transition state, and this results in products being formed but then crosses the activation barrier again, thus reverting back to the reactants (barrier crossing). The higher value of momentum means the H2 molecule (reactant AB) has greater vibrational energy hence the relatively high amplitude oscillation in the BC bond distance. |
| -2.5 | -5.2 | Reactive |  |
The energy of the reactants is very high and the system follows a trajectory which passes thought the transition state and then loops back around and passes through the transition state again before proceeding to the products. The higher value of momentum means the H2 molecule (product BC) has greater vibrational energy hence the relatively high amplitude oscillation in the AB bond distance. |
Transition State Theory
Transition state theory (TST) can be used to predict the rates of reactions. The main assumption of TST is that the rates of chemical reactions can be determined by modelling the motion of particles using classical mechanics, and that that the requirement for reaction is that the reactants must have sufficient energy to access the transition state. Although TST does not consider quantum mechanical effects such as quantisation of energy and tunnelling, it should yield values for the rate of reaction which are in relatively good agreement with experimental reaction rates, as these quantum mechanical effects are only significant at the electron-scale, so for the reactions involving atoms and molecules which are much heavier than electrons, TST should be valid.
(Does TST account for barrier recrossing, do your simulations? Lt912 (talk) 08:19, 9 June 2017 (BST))
F - H - H system
Reaction energetics
The H + HF reaction is endothermic, whereas the F + H2 reaction is exothermic. This is due to the fact that the H-F bond is stronger than the H-H bond. In the reaction of H with HF less energy is gained from forming the H-H bond than is required to break the H-F bond, hence this reaction is endothermic. The reverse is true for the reaction of F and H2, and hence this reaction is exothermic.
Transition State Positions
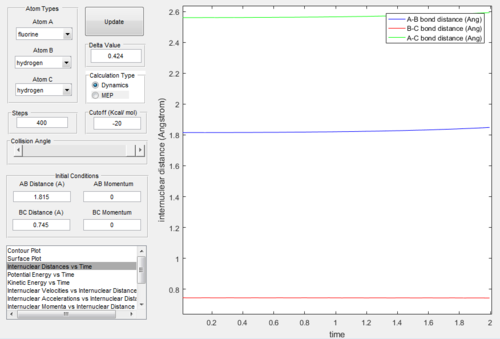
Both the F + H2 and H + HF reactions got through a common transition state [H-H-F] where:
Rts (H-H) = 0.745 Å
Rts (H-F) = 1.815 Å
At this location on the potential energy surface the inter nuclear distances are roughly constant with time, indicating it is the transition state position.
Activation Energies
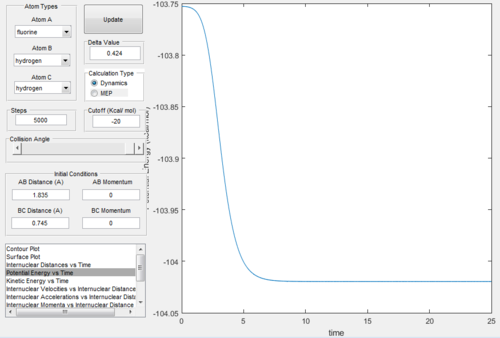
For H2 + F the activation energy Ea = 0.2 kcal/mol
For the reverse reaction of H + HF Ea = 30.2 kcal/mol
The activation energy for the reaction of H with HF is much higher as it involves breaking the strong H-F bond, compared to the reaction of F with H2 which has a lower activation energy due to the fact that in this reaction the weaker H-H bond is broken. The activation energies were determined using an mep calculation by taking the difference between the transition state potential energy and reactants potential energy for both reactions, using the potential energy vs time curve.
Mechanism of release of the reaction energy
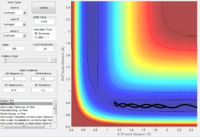
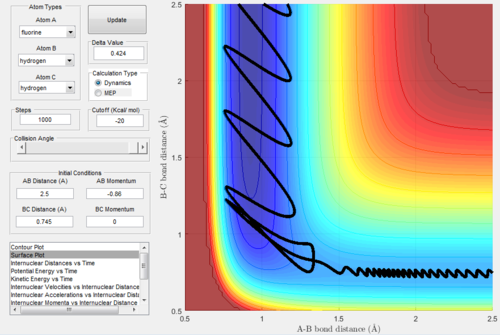
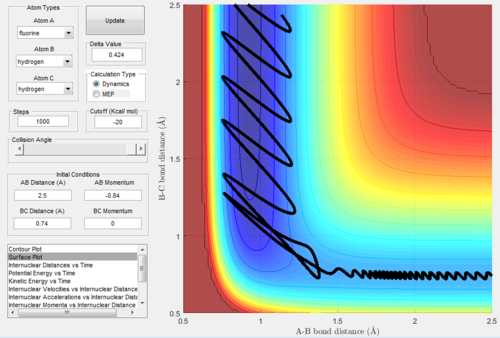
The parameters employed to obtain a reactive trajectory for the H2 + F system was: RH-H = 0.745 Å, RH-F = 2.5 Å, PH-H = 0 and PH-F = -0.86
In the reaction of F with H2 the translational energy of the attacking F atom is converted to vibrational energy in the product, which ensures that energy is conserved. However as the product H-F is in a highly excited vibrational state, it will rapidly undergo internal virbational relaxation to the vibrational ground state, following the reaction dissipating the excess energy as heat. This could be confirmed experimentally possibly by performing IR spectroscopic analysis of the reaction, or alternatively measuring temperature to detect heat changes.
(what about potential energy? Lt912 (talk) 08:20, 9 June 2017 (BST))
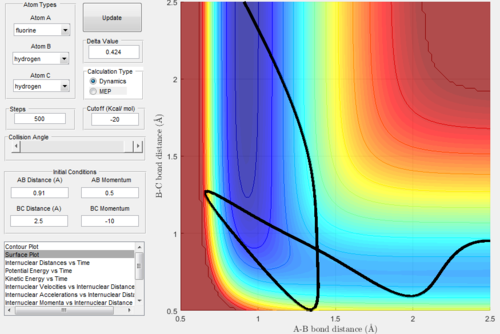
Reaction Dynamics
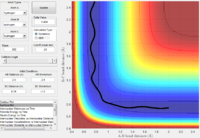
Polanyi's empirical rules empirical rules states that for a reaction in which the transition state is early (i.e. exothermic) the greater translational energy, compared to the virbrational energy, the higher the efficiency of the reaction. The reverse is true for reactions (e.g. endothermic) in which the transition state is achieved later, in this case greater vibrational energy, rather than translational energy, will lead to greater reaction efficiency.
For H2 + F the reaction is exothermic and consequently the transition state is early, consequently in order to obtain a reactive trajectory a high translational energy and low vibrational energy contribution is required. In this matlab model vibrational energy is reduced by lowering pHH (the momentum of the H2 molecule thus giving it lower vibrational energy) and translational energy is increased by increasing pHF momentum term (which effectively increases the translational energy of the incoming F atom).
For HF + H the reaction is endothermic so therefore the transition state is late, therefore in this case to obtain reactive trajectories the translational energy must be reduced whilst increasing the vibrational energy. This is done in matlab by increasing the momentum of the HF molecule (pHF), and the deceasing pHH which reduces the momentum of the incoming H atom, thus decreasing its translational energy.
