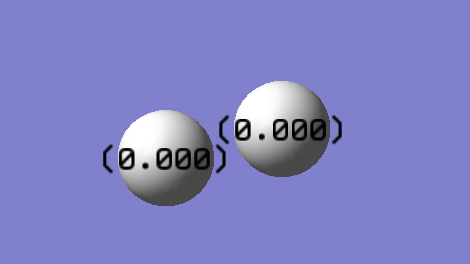ABCD
THE STUDY OF IMPOSED MOLECULES
THE NH3 MOLECULE
Bond distance
N-H bond distance= 1.01798 Å
Bond angle
H-N-H bond angle= 105.741 degrees
Tables of optimisation
Table representing the summary of the optimisation on NH3
| Informations | Values |
|---|---|
| Molecule | NH3 |
| Calculation method | RB3LYP |
| Basis set | 6-31G(d.p) |
| Final energy | -56.55776873 |
| RMS gradient | 0.00000485 |
| point | groupC3V |
Table representing the values found when optimising the NH3 molecule
Item Value Threshold Converged?
Maximum Force 0.000004 0.000450 YES
RMS Force 0.000004 0.000300 YES
Maximum Displacement 0.000072 0.001800 YES
RMS Displacement 0.000035 0.001200 YES
Predicted change in Energy=-5.986259D-10
Dynamic image of the optimised NH3 molecule
test molecule |
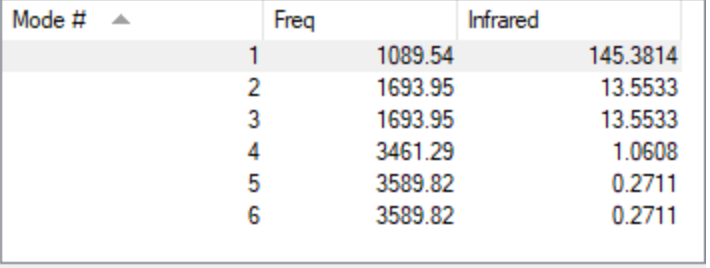
Table representing the different vibrational frequencies of the NH3 molecule
Please find all the informations regarding the optimised NH3 molecule here
Frequency analysis
Table showing the frequency analysis for the optimised NH3 molecule
| WAVENUMBERS | 1090 | 1693 | 1693 | 3461 | 3590 | 3590 |
| SYMMETRY | A1 | E | E | A1 | E | E |
| INTENSITY | 145 | 14 | 14 | 1 | 0 | 0 |
| IMAGE | .png) |
.png) |
.png) |
.png) |
 |
.png)
|
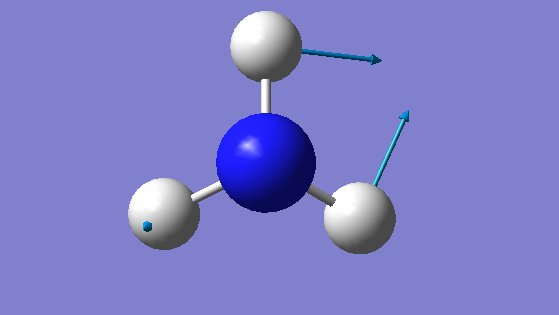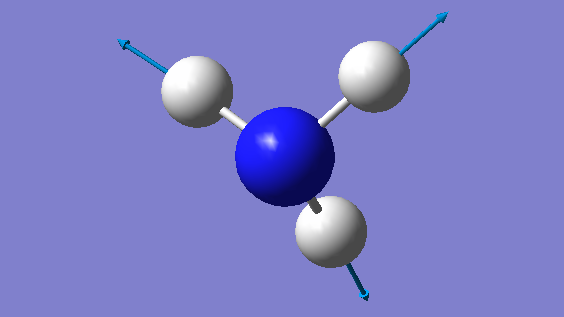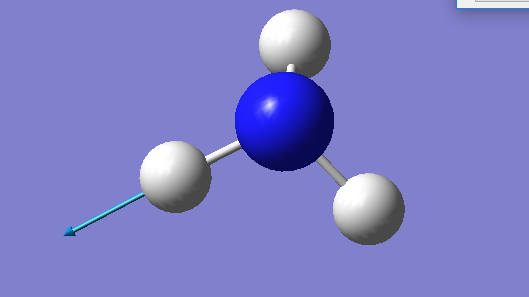Animating vibrations
We would expect 6 different vibrational modes (because 3 x 4 -6 = 6). There are two degenerate bond stretching frequencies and two degenerate stretching frequencies. We can observe 3 bending modes and 3 stretching modes. The bending modes are at 1090 , 1693 and 1693 cm-1 and the stretching modes are at 3461 ,3590 and 3590 cm-1.
The mode having a frequency of 3461 cm-1 is highly symmetric.
The mode having a frequency of 1090 cm-1 is known as the umbrella mode. We would expect to see three bands in the spectrum of gaseous ammonia because there are two pairs of degenerate frequencies that make up two bands (1693 and 3590 cm-1) and finally one band (1090 cm-1) that is not degenerate, that is visible in the spectrum. We can neglect the frequency at 3461 cm-1 as its intensity is 1.
Atomic charges
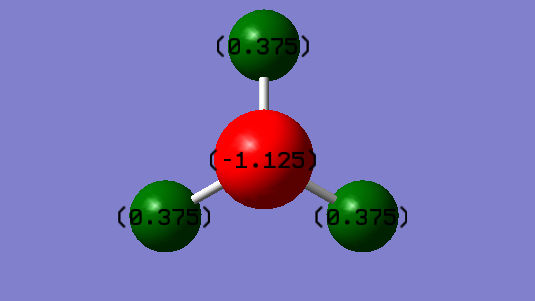
Image showing the distribution of the charges on each atom in the NH3 molecule
The charge on Nitrogen is -1.125 and the charge on the hydrogen atoms are 0.375. We would expect the charge on nitrogen to be negative as this atom is more electronegative than hydrogen and therefore the hydrogen atoms to be positively charged as they are more electropositive. Furthermore, the lone pair of electrons on the N-atom creates a partial negative charge. Since a NH3 molecule is neutral, the partial negative charge on the N-atom must be balanced out by positive charges of the H-atoms, hence the hydrogen atoms are positively charged.
THE H2 MOLECULE
Bond distance
H-H bond distance= 0.6 Å
Bond angle
H-H bond angle= 180 degrees
Tables of optimisation
Table representing the summary of the optimisation on H2
| Informations | Values |
|---|---|
| Molecule | H2 |
| Calculation method | RB3LYP |
| Basis set | 6-31G(d.p) |
| Final energy | -1.17853935735 |
| RMS gradient | 0.00000017 |
| point | group D*H |
Table representing the values found when optimising the H2 molecule
Item Value Threshold Converged? Maximum Force 0.000000 0.000450 YES RMS Force 0.000000 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000001 0.001200 YES Predicted change in Energy=-1.164080D-13
Dynamic image of the optimised H2 molecule
test molecule |
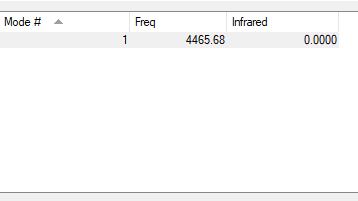
Table representing the different vibrational frequencies of the H2 molecule
.png)
Please find all the informations regarding the optimised H2 molecule here
Frequency analysis
Table showing the frequency analysis for the optimised H2 molecule
| WAVENUMBERS | 4465 |
| SYMMETRY | SGG |
| INTENSITY | 0 |
| IMAGE | .png)
|
Animating vibrations
We would expect the H2 molecule to have 1 vibrational mode because it is linear therefore 3N-5= 3x 2 -5= 1. We do not observe any degeneracy for this molecule as there only one vibrational mode. We can observe that this vibrational mode is a stretching frequency. No modes are highly symmetrical as there is only one vibrational frequency. We would as a consequence observe no bands in its spectrum as its only vibrational mode has an intensity of 0 .
Atomic charges
Image showing the distribution of the charges on each atom in the H2 molecule
We can observe that the two hydrogen atoms have no charge this is because they are the same atoms.
THE N2 MOLECULE
Bond distance
N-N bond distance= 1.09200 Å
Bond angle
N-N bond angle= 180 degrees
Tables of optimisation
Table representing the summary of the optimisation on N2
| Informations | Values |
|---|---|
| Molecule | N2 |
| Calculation method | RB3LYP |
| Basis set | 6-31G(d.p) |
| Final energy | -109.524128676 |
| RMS gradient | 0.00000060 |
| point | group D*H |
Table representing the values found when optimising the N2 molecule
Item Value Threshold Converged?
Maximum Force 0.000001 0.000450 YES
RMS Force 0.000001 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000000 0.001200 YES
Dynamic image of the optimised N2 molecule
test molecule |
Table representing the different vibrational frequencies of the N2 molecule
.png)
Please find all the informations regarding the optimised N2 molecule here
Frequency analysis
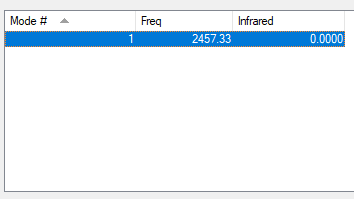
Table showing the frequency analysis for the optimised N2 molecule
| WAVENUMBERS | 2457 |
| SYMMETRY | SGG |
| INTENSITY | 0.000 |
| IMAGE | .png)
|
Animating vibrations
We would expect the N2 molecule to have 1 vibrational mode because it is linear therefore 3N-5= 3x 2 -5= 1. We do not observe any degeneracy for this molecule as there only one vibrational mode. We can observe that this vibrational mode is a stretching frequency. No modes are highly symmetrical as there is only one vibrational frequency. We would as a consequence observe no bands in its spectrum as its only vibrational mode has an intensity of 0.
Atomic charges
Image showing the distribution of the charges on each atom in the N2 molecule
We can observe that the two nitrogen atoms have no charge this is because they are the same atoms.
THE MONO-METALLIC TRANSITION METAL COMPLEX
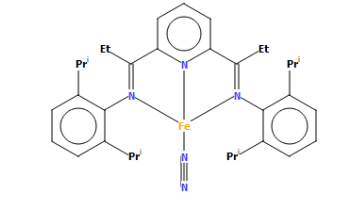
The chosen mono-metallic transition metal complex that coordinates N2 has the unique identifier BARTOF This molecule is also known as (dinitrogen)-(2,6-bis(1-(2,6-diisopropylphenylimino)propyl)pyridine)-iron.
If you wish to read more about this particular mono-metallic transition metal, you can read this:here
Image of the mono-metallic transition metal complex: the (dinitrogen)-(2,6-bis(1-(2,6-diisopropylphenylimino)propyl)pyridine)-iron molecule
.png)
The two bond lengths between the two N atoms are 1.112 Å and 1.09200 Å (our measured value). We can observe a difference between the two bond lengths. Indeed, the measured value is lower than the value of the transition metal complex, this due to electron density being pulled away from the triple bond of dinitrogen. The reason for a longer N-N triple bond in the transition metal is the strength of the bond. Since the nitrogen atom has a positive charge (N+) because it has 4 bonds (three to the nitrogen and one to the iron Fe), there is less electron density surrounding the atom. As a consequence, the triple bond between the two nitrogens has less electron density, and is weaker. Since the triple bond has less electron density, the two nitrogen atoms are held less tightly together by the electrons, therefore the bond is longer. However, for our N2 molecule, the bond length is shorter because it has three bonds. The electron density surrounding the two nitrogens is more important, therefore they are held together more tightly. The bond is shorter.
THE HABER-BOSCH REACTION
N2 + 3H2 -> 2NH3
E(NH3)= -56.5577687 u.a.
2*E(NH3)= 2 x -56.5577687 u.a = -113.1155374 u.a.
E(N2)= -109.5241286 u.a.
E(H2)= -1.1785394 u.a.
3*E(H2)= 3 x -1.1785394 u.a. = -3.5356182 u.a.
ΔE=2*E(NH3)-[E(N2)+3*E(H2)]= -113.1155374 -[- 109.5241286 -3.5356182] = -0.0557506 u.a.
ΔE= 2625.5 x - 0.0557506 = - 146.4 kJ.mol-1
Thus the energy of the Haber-Bosch reaction is - 146.4 kJ.mol-1. The energy is negative as the product is more stable because the reaction is exothermic. Indeed, from this reaction, we can conclude that the 2 NH3 (the product) is the most stable as it has the lowest energy (-113.12 u.a.) compared to the reactants.
THE STUDY OF THE CHOSEN MOLECULE
THE CO2 MOLECULE
Bond distance
The bond distance between C=O is 1.25840 Å
Bond angle
The bond angle of O=C=O is 180 degrees because it is linear.
Tables of optimisation
Table representing the summary of the optimisation on CO2
| Informations | Values |
|---|---|
| Molecule | CO2 |
| Calculation method | RB3LYP |
| Basis set | 6-31G(d.p) |
| Final energy | -188.58093945 |
| RMS gradient | 0.00001154 |
| point | group D*H |
Table representing the values found when optimising the CO2 molecule
Item Value Threshold Converged? Maximum Force 0.000024 0.000450 YES RMS Force 0.000017 0.000300 YES Maximum Displacement 0.000021 0.001800 YES RMS Displacement 0.000015 0.001200 YES Predicted change in Energy=-5.259645D-10
Dynamic image of the optimised CO2 molecule
test molecule |
Table representing the different vibrational frequencies of the CO2 molecule
.png)
Please find all the informations regarding the optimised CO2 molecule here
Frequency analysis
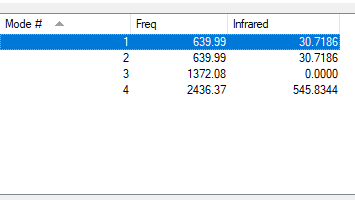
Table showing the frequency analysis for the optimised CO2 molecule
| WAVENUMBERS | 640 | 640 | 1372 | 2436 |
| SYMMETRY | PIU | PIU | SGG | SGU |
| INTENSITY | 31 | 31 | 0 | 546 |
| IMAGE | .png) |
.png) |
.png) |
.png)
|
Animating vibrations
We would expect the CO2 molecule to have 4 vibrational modes because it is linear therefore 3N-5= 3x 3 -5= 4. We observe degeneracy for this molecule as there are four vibrational modes, and some have the same frequency. Therefore we can see that there are two vibrational modes that have a frequency of 640cm-1: they are degenerate. Moreover, the vibrational mode at 1372 cm-1 has zero intensity. So it will not be observed. We can observe two bending (640 and 640 cm-1) and two stretching modes (1372 and 2436 cm-1). The vibrational mode that is highly symmetrical is the one at a frequency of 1372 cm-1. We would as a consequence only observe two bands in its spectrum.
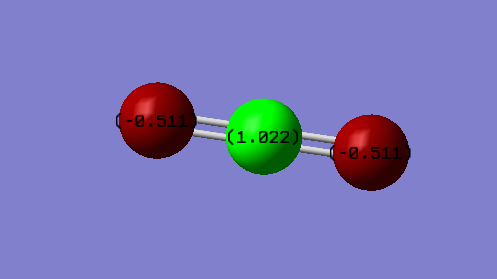
Atomic charges
Image showing the distribution of the charges on each atom in the CO2 molecule
.png)
The charge on carbon is 1.022 and the charge on the oxygen atoms are -0.511. We would expect the charge on the oxygen atoms to be negative as these atoms are more electronegative than carbon and therefore the carbon atom to be positively charged as it is more electropositive. Furthermore, the lone pairs of electrons on the O-atom create a partial negative charge. Since a CO2 molecule is neutral, the partial negative charges on the O-atoms must be balanced out by a positive charge of the C-atom, hence the carbon atom is positively charged.
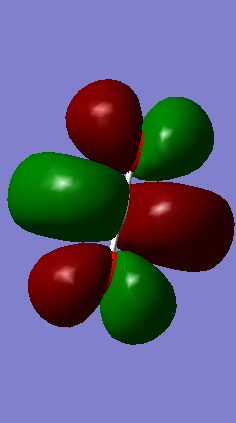
Molecular orbitals
Table showing the MO analysis for the optimised CO2 molecule
| Contribution of MO | 2p(x) of oxygen and 2p(x) of carbon | 2p(x) of oxygen | 2p(z) of carbon and 2p(z) of oxygen | 2s of oxygen | The 2s of carbon and 2p(z) of oxygen orbitals |
| Energy (cOmpared to the HOMO) | high in energy | HOMO | slightly deep in energy | deep in energy | deep in energy |
| Type of bonding | bonding | non-bonding | bonding | non-bonding | bonding |
| Occupied? | yes | yes | yes | yes | yes |
| Effect | pi bonding | lone pair | sigma bonding | lone pair | sigma bonding |
| IMAGE | .png) |
.png) |
.png) |
.png) |
.png)
|
Image of the LUMO of CO2
.png)
COMPARISION OF CO2 WITH SiO2
Bond distance of SiO2
The bond length of Si=O is 1.51970 Å.
Bond angle of SiO2
The bond angle of O=Si=O is 180 degrees.
Tables of optimisation of SiO2
Table representing the summary of the optimisation on SiO2
| Informations | Values |
|---|---|
| Molecule | SiO2 |
| Calculation method | RB3LYP |
| Basis set | 6-31G(d.p) |
| Final energy | -439.92811459 |
| RMS gradient | 0.00003590 |
| point | group D*H |
Dynamic image of the optimised SiO2 molecule
test molecule |
Please find all the informations regarding the optimised SiO2 molecule here
Comparision of the bond length between the CO2 molecule and the SiO2 molecule
We can observe that the bond length for the SiO2 (1.51970 Å) molecule is longer than the CO2 molecule (1.25840 Å). We can observe a difference between the two bond lengths. This due to electron density being pulled away from the double bond. The reason for a longer Si-O double bond is the strength of the bond. Indeed, the Si=O (638 kJ.mol-1) bond is lower in energy than the C=O (805 kJ.mol-1) this is because of the less favourable orbital overlap between the Si atom and the O atom than between the C atom and the O atom. For the Si=O, the 2p of the oxygen atom overlaps with the 3p of the Si atom (as it is on the 3rd row of the periodic table, ie a row below carbon and oxygen); whilst for the C=O, the 2p of the oxygen overlaps with the 2p of the carbon. Hence there is a better overlap of the orbitals and the C=O is shorter than Si=O. Furthermore, carbon is more electronegative than Si, therefore the the C=O will have more ionic character than the Si=O. This will result in a shorter bond length as the atoms are more tightly bounded to each other.
Marking
Note: All grades and comments are provisional and subjecct to change until your grades are officially returned via blackboard. Please do not contact anyone about anything to do with the marking of this lab until you have recieved your grade from blackboard.
Wiki structure and presentation 0.5/1
Is your wiki page clear and easy to follow, with consistent formatting?
YES
Do you effectively use tables, figures and subheadings to communicate your work?
YES - however, all your jmols are labelled as 'test molecule' which is not informative at all
NH3 0.5/1
Have you completed the calculation and given a link to the file?
YES
Have you included summary and item tables in your wiki?
YES
Have you included a 3d jmol file or an image of the finished structure?
YES
Have you included the bond lengths and angles asked for?
YES
Have you included the “display vibrations” table?
YES
Have you added a table to your wiki listing the wavenumber and intensity of each vibration?
YES
Did you do the optional extra of adding images of the vibrations?
YES
Have you included answers to the questions about vibrations and charges in the lab script?
YES, You correctly stated that there are two sets of degenerate modes - this explains a spectrum with 4 peaks. However there are only 2 peaks visible as peaks 4, 5 and 6 are of too low an intensity to be visible.
N2 and H2 0/0.5
Have you completed the calculations and included all relevant information? (summary, item table, structural information, jmol image, vibrations and charges)
YES - However, the stated lengths are the ones of your initial structure and not the ones of your optimised molecules! You have stated bond angles for diatomic molecule. To define a bond angle a minimum of 3 atoms is needed!
Crystal structure comparison 0.5/0.5
Have you included a link to a structure from the CCDC that includes a coordinated N2 or H2 molecule?
YES
Have you compared your optimised bond distance to the crystal structure bond distance?
YES
Haber-Bosch reaction energy calculation 1/1
Have you correctly calculated the energies asked for? ΔE=2*E(NH3)-[E(N2)+3*E(H2)]
YES
Have you reported your answers to the correct number of decimal places?
YES
Do your energies have the correct +/- sign?
YES
Have you answered the question, Identify which is more stable the gaseous reactants or the ammonia product?
YES
Your choice of small molecule 4/5
Have you completed the calculation and included all relevant information?
YES
Have you added information about MOs and charges on atoms?
You have done a good job of presenting this information, well done! You identified the contributing AOs correctly. you could have analysed the MOs in more depth.
Independence 1/1
If you have finished everything else and have spare time in the lab you could: Check one of your results against the literature, or Do an extra calculation on another small molecule, or
YES - well done!
Do some deeper analysis on your results so far