3rd Year Computational Chemistry: Module 1 (gc2109)

By Gen Cross

In recent years the usefulness and importance of computational chemistry has increased greatly, mostly in line with the exponential increase computing power available to carry out these calculations. It seems sure that in the next decade the predictions made by computational chemistry will be gain the ability to carry out calculations on more complex molecules and to a higher accuracy with ever greater advances in technology.

This wiki aims to illustrate the potential of these calculations to make reliable predictions for the major product of reactions and their conformation. Allinger's MM2 force field calculations which are based on molecular mechanics takes into account 5 interactions (diatomic bond stretches, triatomic bond bends, tetra-atomic bond torsions, Van der Waals repulsions and electrostatic attractions of bond dipoles) in a molecule and minimizes the sum of these to produce a total energy. This model only takes into a account steric interactions and is unable to break or create bonds as it does not account for semi-empirical molecular orbitals. As a result in situations where charges and lone pairs are significant for the stabilization of certain conformations of a molecule the MOPAC method may give a more accurate result since this is a semi-empirical molecular orbital method. There are advantages and disadvantages to both methods and often using both in combination provides the most comprehensive results.

Structure and Spectroscopy by Gen Cross

The Hydrogenation of Cyclopentadiene Dimer

Introduction

The dimerisation of cyclopentadiene proceeds in a concerted [4_πs +2_πs] fashion, and is a good example of a Diels-Alder reaction. It has been well documented in literature that this class of reactions produces the endo isomer as the major product at room temperature, to a high selectivity. In this example molecular mechanics will be used to show that the endo product is in fact a higher energy conformation than the exo product to confirm that the reaction is under kinetic control at room temperature.

Formation of Cyclopentadiene

It is possible for the two cyclopentadiene molecules to dimerise because they can act as both electrophiles and nucleophiles, i.e. it is possible for one molecule to behave as the electron rich diene, while the other acts as the dienophile. This is made possible by the molecular orbitals cyclopentadiene has: 3 p bonding orbitals delocalised over the 5 carbon atoms. The top 2 p bonding orbitals (ψ2 + ψ3) are degenerate and are the HOMO’s, used by the diene. The electrons are reacted with the degenerate LUMO’s (ψ4 + ψ5) of the dienophile cyclopentadiene. Low lying bonding orbital ψ1 is not involved in the reaction.

The dimerisation of the two cyclopentadiene rings to produce both the endo and exo isomers is shown below.

Figure 1 - Dimerisation of Cyclopentadiene

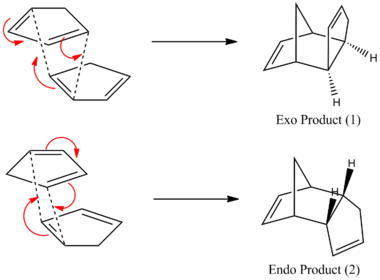
Having drawn out each of the isomers on ChemBio3D Ultra their geomteries were optimized using MM2 and the results of this can be seen in Table 1. It is clear from this analysis that the exo isomer is more stable since it's total energy is around 2 kcal mol^-1 lower in energy. This makes it clear that the reaction is under kinetic control at room temperature; if the temperature was increased sufficiently the activation energy barrier for the exo product would be over come and an equilibrium would exist in which the lower energy exo product would dominate. It is not possible to show this using Molecular Mechanics since it can not analyse the energy of transition states but this has been well documented in literature: Woodward and Hoffman showed that the endo transition state benefits from stabilising p orbital interactions between the 2 Cp rings which grealty over rides steric clashing caused by the proximity of the 2 Cp rings.

Table 1 - MM2 energy values of the different interactions for both isomers

Type of Interaction (kcal mol-1)	exo- Isomer (1)	endo- Isomer(2)	Difference (exo-endo)
Stretch	1.29	1.25	0.04
Bend	20.58	20.84	- 0.26
Stretch-Bend	- 0.84	- 0.84	0.00
Torsion	7.66	9.51	- 1.85
Non-1,4 VDW	- 1.42	- 1.54	0.12
1,4 VDW	4.23	4.32	- 0.09
Dipole/Dipole	0.38	0.45	- 0.07
Total Energy	31.88	34.00	- 2.12

A closer look at the breakdown of the energy differences reveals that the main contribution to this difference is torsion. This difference in torsional strain comes from the difference in the amount of steric clashing between Hydrogen atoms in each of the isomers. In the Endo-isomer the Hydrogen atoms on the newly formed C-C bond are forced closer together than the Exo-isomer which has a far more favourable staggered conformation. It can be seen in the 3D (Jmol) views and in Figure 1 that the Endo-isomer also suffers from steric clashing between the bridge-end Hydrogens and the 2 Hydrogens on the C-C bond of what was the dienophile cylcopentadiene. Both of these steric clashes cause the torsional strain to be higher in the Endo-isomer.

Hydrogenation of the Endo Product

The kinetic product of the reaction above can be hydrogenated at either of the alkenes in the pentene ring to forming Product (3) or at the hexene ring forming Product (4).

Figure 2 - Hydrogenation of Endo Product

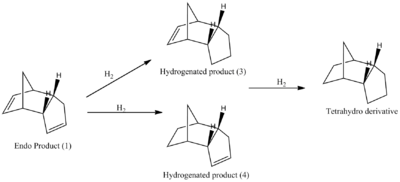
MM2 calculations were run over both the hydrogenated product structures to show which is the most thermodynamically stable product.

Table 2 - MM2 energy values of the - Hydrogenated Product (3) and Hydrogenated Product (4)

Type of Interaction (kcal mol-1)	Hydrogenated Product (3)	Hydrogenated Product (4)	Difference (Product (3) - Product (4))
Stretch	1.28	1.10	0.18
Bend	19.87	14.52	5.35
Stretch-Bend	-0.83	-0.55	-0.28
Torsion	10.81	12.50	-1.69
Non-1,4 VDW	-1.23	-1.07	-0.16
1,4 VDW	5.63	4.51	1.12
Dipole/Dipole	0.16	0.14	0.02
Total MM2 Energy	35.67	31.15	4.52

It is clear from the above that Hydrogenated Product (4) is the more stable, thermodynamic product since it is 4.52kcal mol^-1 lower in energy than Product (3) . The bending interaction is the major contributor to this difference in energy, along with 1,4 Van der Waals interactions which provide a smaller difference in stability. But it can also be seen from the Table 3 that torsional strain is higher in Product (4). With the aid of the Jmols of each of the products and the figures below it is clear to see where the difference in the Bend energies comes from. The ideal geometry for an sp2 hybridised centre is 120^°, deviations from this ideal angle will cause an increase in the Bend energies seen in the MM2 calculations. Product (3) has angles of 107.8 and 107.8^° compared to 112.4^° and 113^° in Product (4), although both structures have considerable strain the former has a more compressed bond angle and so has a higher bend energy (4.52kcal mol^-1). It is also important to note that more important than the nominal values for the Bend energies for each of the Products is their energies relative to the original Endo isomer with 2 alkene moieties which has an original Bend energy of 20.85kcal mol^-1. Clearly a reduction in Bend energy to 19.87kcal mol^-1 (for Hydrogenated Product (3)) is very small, which suggests strongly that most of the strain in structure is located in the alkene next to the bridge-end carbon. It can be concluded it is for this reason that the hydrogenation of the Endo isomer shows regioselectivity for the alkene closer to the carbon bridge, and so selectively produces Hydrogenated Product (4) before reacting again to form the tetrahydroderivative.

Figure 3 - Alkene bond angle for Hydrogenated Product (3)

Figure 4 - Alkene bond angle for Hydrogenated Product (4)

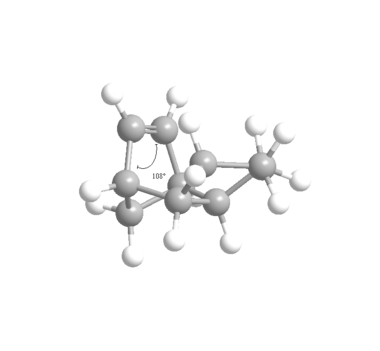
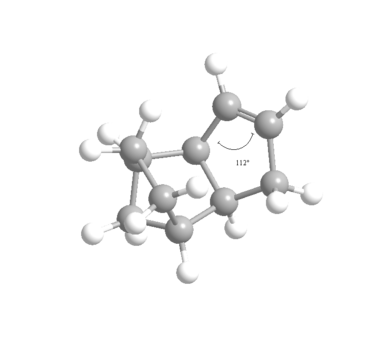
It can be seen from the Jmol diagrams that in Product (3) the orange Hydrogen atoms suffer from steric clashing with eachother because the alkene double bond forces the hydrogen into an unfavourable positon. In Product (4) this is avoided since the hydrogenation has taken place at the alternative alkene and so the sp3 hybridised carbon atoms holds the Hydrogen atoms in a lower energy conformation. This reveals the reason for the higher 1,4 Van der Waals energy seen in Product (3) in the MM2 calculations.

Stereochemistry and Reactivity of an Intermediate in the Synthesis of Taxol

Introduction

Taxol is one of the biggest selling anticancer drugs in history, its action is known to be anti-mitotic due to its ability to promote the assembly of tubulin. It is mainly used to treat ovarian and breast cancers.

Figure 5 - Two possible atropisomeric intermediates in the synthesis of Taxol

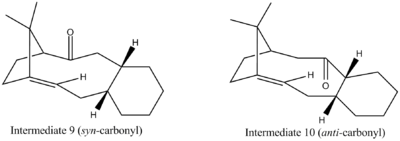
Above are the 2 possible intermediates in the synthesis of Taxol. This is an example of atropisomerism , which describes a situation in which there are 2 long lived isomers which have a high barrier to interconversion most commonly due to restricted rotation about a single bond due to a large sterically hindered group or a ring structure that leads to a conformational lock. Molecular mechanics will be used to determine which of these isomers is more thermodynamically more stable and therefore the isomer that is predominantly involved in the synthesis of Taxol. When left at room temperature a racemic mixture of the 2 isomers will eventually produce only 1 of the geometries exclusively, either carbonyl up (syn)(intermediate 9) or carbonyl down (anti)(intermediate 10).

Results and Discussion

Each Taxol intermediate can exist in 2 different geometries, one with a chair conformation for the cyclohexane ring and another with a twist boat. The chair conformation has lower energy for both intermediates. Each of the structures were again drawn in ChemBio 3D and their energies minimized using MM2 calculations. On minimizing the energies of both intermediate structures, false minima were found, corresponding the aforementioned alternative twist boat conformers. The cyclohexane rings were therefore ‘pulled’ into exaggerated chair conformations to find the true energy minima for both intermediates. The twist boat energy parameters have been included below for fullness, however due to their energies being around 5kcal mol^-1 higher in energy it is believed that in reality these conformers would be very short lived. Both MM2 and MMFF94 calculations were run over syn and anti isomers. It can be seen from the data below that by enlarge both methods show similar results. However the MMFF94 calculations are more complex and advanced than the MM2 calculations because it takes into consideration electrostatic interactions such as intermolecular and intramolecular interactions whereas the MM2 force field treats everything as a classical two-body spring potential. The MMFF94 is the first in the family of (Merck Molecular Force Field) MMFF which were developed by Merck Research Labs. They are not tailored for use with any particular type of molecule but perform well with a wide range of organic molecules.

Table 3 - MM2 and MMFF94 energy values of the - Intermediate 9 (chair), Intermediate 9 (twist-boat), Intermediate 10 (chair) and Intermediate 10 (twist-boat)

Type of Interaction (kcal mol-1)	Intermediate
	9 (syn-Carbonyl, chiar)	9 (syn-Carbonyl, twist-boat)	10 (anti-Carbonyl, chiar)	10' (anti-Carbonyl, twist-boat)	Difference (9 chair - 10 chiar)
Stretch	2.78	2.88	2.62	2.71	0.07
Bend	16.54	17.28	11.34	11.83	5.20
Stretch-Bend	0.43	0.47	0.34	0.39	0.09
Torsion	18.26	20.6	19.67	22.89	-1.41
Non-1,4 VDW	-1.56	-0.89	-2.16	-1.99	0.60
1,4 VDW	13.11	14.37	12.87	14.33	0.24
Dipole/Dipole	-1.72	-1.71	-2.00	-2.00	0.28
Total MM2 Energy	47.84	53.01	42.68	48.16	5.07
Total MMFF94 Energy	76.19	84.26	66.13	72.05	10.06

Despite the differences in the 2 methods the structures produced by running each of the force fields were largely the same. It can also be seen from the above data that they are in agreement: the anti-intermediate (10) is the thermodynamically more stable product. In conclusion although the MM2calculations are simple they are in this case sufficiently accurate since there are no formal charges in the structure. The result that the anti isomer is lower in energy is to be expected since it does not suffer from the unfavourable steric crowding and Van der Waals interactions between the carbonyl oxygen and the bridge-end carbon and hydrogens that the syn isomer does. A closer look at the breakdown of energies in the MM2 calculations revelas the biggest difference in energy is due to a bending interaction. It can be seen from the Jmol diagrams that the syn isomer has an angle of 125^° for the sp2 hybridised carbon, whereas the anti-isomer has angle far closer to the ideal 120^°, at 119.7^°.

Hyperstable Alkenes

It has been noted in literature that the functionalisation of the alkene in the Taxol intermediate is extremely slow. In this section computational methods will be used to find why this is the case.

Table 4 - MM2 and MMFF94 energy values of Intermediate 10 (chair) and Hydrogenated Intermediate 10 (chiar)

Type of Interaction (kcal mol-1)	Intermediate
	10 (with alkene)	10' (alkene hydrogenated)	Difference (10 chair - 10 hydrogenated alkene)
Stretch	2.62	2.85	-0.23
Bend	11.34	14.23	-2.89
Stretch-Bend	0.34	0.67	-0.33
Torsion	19.67	22.12	-2.45
Non-1,4 VDW	-2.16	-2.67	0.51
1,4 VDW	12.87	15.89	-3.02
Dipole/Dipole	-2.00	-1.73	-0.27
Total MM2 Energy	42.68	51.36	-8.68
Total MMFF94 Energy	66.13	72.30	-6.17

It can be seen from both the MM2 and MMFF94 calculations above that the hydrogenation of the Taxol intermediate alkene is thermodynamically unfavourable since the product has an energy around 6kcal mol^-1 higher than the reactant. The main contributions to this energy difference are Bend energy, Torsion and 1,4 Van der Waals interactions. It can be seen from the Jmol diagrams above that the effect of hydrogenating the alkene bond is to change the hybridisation of the carbons from sp2 to sp3, this would be fine but the original sp2 carbons are quite close to the ideal geometry of 120^°, where as the newly formed sp3 carbons are very strained since they are forced and conformationally locked into an angle of 117.8^° by the pentane ring, this angle is far wider than the ideal 109^° for an sp3 hybridised centre. This results in the hydrogenated product being high energy and therefore its formation being slow.

The torsional components of the hydrogenated and non-hydrogenated molecules can be evaluated using the The Olefin Stabilisation energy formula. Olefin stabilisation energy = 19.67 - 22.12 = -2.45kcal mol^-1. This negative value highlights the stability of the alkene.

Regioselective Addition of Dichlorocarbene

Introduction

In this section the orbital control of reactivity of 2 alkene groups in dichlorocarbene is investigated using semiempirical calculations i.e. MOPACwhich moves away from a purely classical treatment and towards a quantum mechanical description. The resulting Molecular Orbital predictions will be used to show why the reaction below shows regioselectivity for the syn alkene (under the chlorine atom) rather than the antialkene.

Figure 6 - Mechanism for Carbenylation

Figure 7 - Symmetry Elements of Dichlorocarbene = E and σ_h

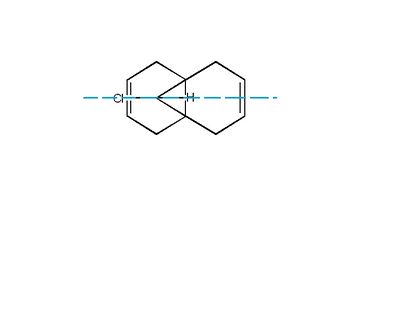
The symmetry elements give the Dichlorocarbene molecule the Point Group= C_s. The σ_h symmetry plane should mean the molecular orbitals for the molecule also have symmetry along this plane.

Part 1 - Orbital control of Reactivity

Initially the energy of structures were minimized using MM2 and then minimized again using MOPAC/ PM6, to produce molecular orbitals for the Dichlorocarbene. However it was found when using the PM6 calculations that the molecular orbitals produced were not very symmetrical and it is believed that there is a bug in ChemBio 3D which causes the PM6 minimization to produce a structure for dichlorocarbene which is not symmetrical which means the orbitals are not symmetrical as a result.

As an alternative the AM1 method was used and this produced far more satisfactory results and agreed well with the orbitals produced by purely quantum mechanical calculations in GaussView 5.0. These can be seen below.

Table 5 - Molecular Orbitals for Dichlorocarbene

Molecular Orbital	Method
	MOPAC / AM1	GaussVeiw 5.0
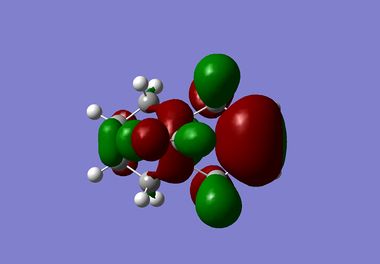
HOMO-1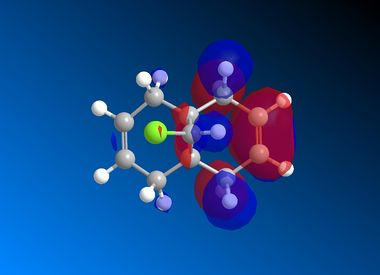
HOMO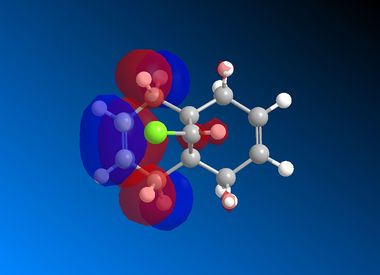
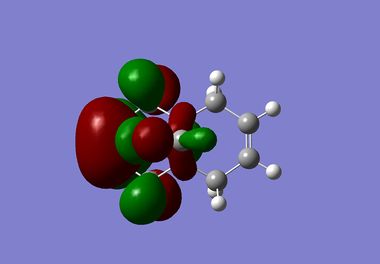LUMO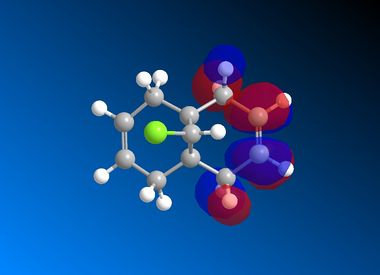
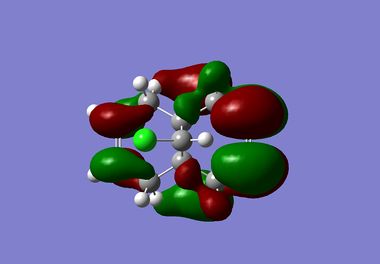LUMO+1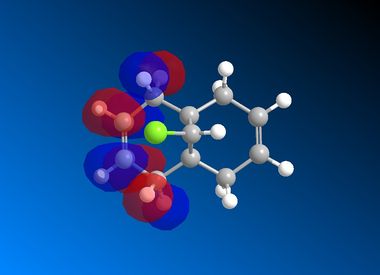
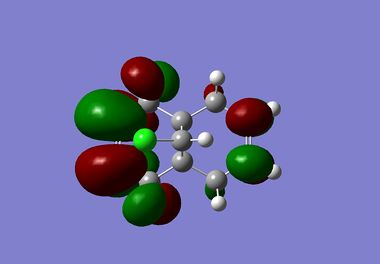LUMO+2		Side on view

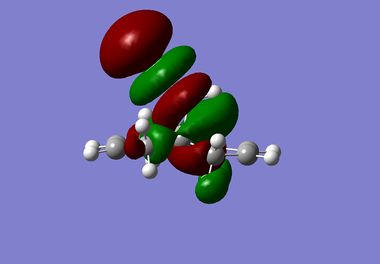It is clear from the results above that both AM1 and GaussView suggest the HOMO for dichlorocarbene is located on the syn alkene. It is this orbital which is most important for the reaction of dichlorocarbene with an incoming electrophile because it is where the electrons of the highest energy are located (i.e. most nucleophilic). This explains the selectivity for the carbenylation of dichlorocarbene for the syn alkene over the anti alkene. There is also an obvious and expected trend in that as you go down the table from HOMO-1 to LUMO+2 the number and size of bonding interactions between orbitals decreases. One very striking molecular orbital is the LUMO+2, it strongly resembles the structure of a σ^* orbital, and it is very likely to be the C-Cl σ^* antibonding orbital. This orbital is a particularly good electron acceptor due to the electronegativity of chlorine making the carbon electron deficient. As a result of this a stabilising interaction is likely to form via donation of electrons from occupied π orbital of the anti alkene into this σ^* orbital. This prediction can be confirmed by use of computational methods, by producing IR spectra for the dichlorocarbene and the monohydrogenated molecule to see the effect on the C-Cl vibrational frequency.

Part 2 - Influence of the Cl-C bond on vibrational frequencies

To analyse the effects of the presence or absence of the anti alkene we must use the Simple Harmonic Oscillator equation: ν = (1/2π)*(k/μ)^0.5 . This shows that as the strength of the bond increases (force contant k), the frequency of its vibration also increases. The IR Spectra below were generated by optimizing the geometries of the molecules by first using MM2, MOPAC, then using the Gaussian geometry optimization. Having found the optimized geometry the molecule was to SCAN to generate a vibrational spectrum on GaussView 5.0.

From the above analyses of the Molecular Orbitals and their locations it is expected that when the anti alkene is hydrogenated, thus removing the stabilising π (C=C) to σ^* (C-Cl) interaction the strength of the C-Cl bond will increase: donation is being made into an antibonding orbital causing the strength and therefore force constant for the C-Cl bond to be reduced, when donation is removed the strength of the bond and so the frequency of vibrational absorption increase. This is indeed found to be the case and is illustrated in the IR spectra shown below.

Figure 8 - Vibrational Spectrum of Dichlorocarbene

Figure 9 - Vibrational Spectrum of Monohydrogenated Dichlorocarbene

Table 6 - Summary of Important Data from the Vibrational Spectra for Dichlorocarbene and Monohydrogenated Dichlorocarbene

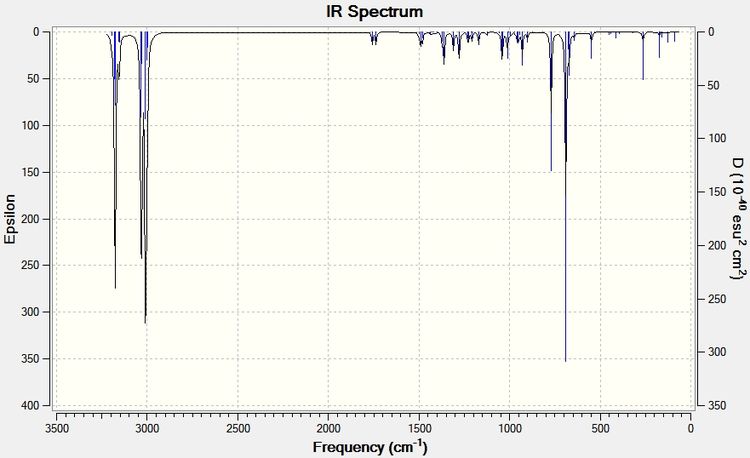
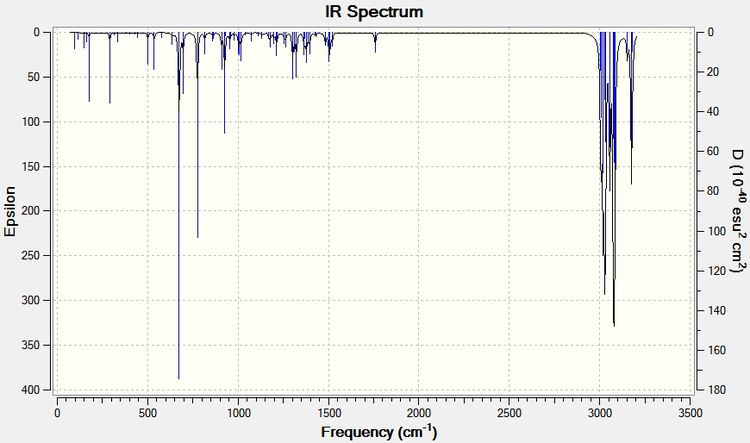
Type of Bond Vibration (cm-1)	Molecule
	Dichlorocarbene	Monohydrogenated Dichlorocarbene
C-Cl	770.85	774.96
C=C (syn)	1757.45	1758.06
C=C (anti)	1737.05	n/a

A difference in the frequency of absorption for the C-Cl bond of around 4cm^-1 is significant and strongly supports the theory that there is an interaction between the anti alkene and C-Cl anti bonding orbital. To further back this analysis of absorption of the same C-Cl bond is carried out with a variety of functional groups which are electron donating and withdrawing below.

Part 3 - Influence of funtionalisation of the Anti double bond

Using the same rationale as above, it is a simple further step to suggest that adding an electron withdrawing group to the anti alkene will also cause the C-Cl bond strength to increase, since some of the electrons in the π (C=C) bond can no longer be donated into to σ^* due to demands of this new group. The opposite will happen when an electron donating group is added.

Table 7 - Summary of Important Data from the Vibrational Spectra for Dichlorocarbene and Monohydrogenated Dichlorocarbene

Type of Bond Vibration (cm-1)	Substituents on Anti alkene
	1 CN Show IR|[9]	2 CN Show IR|[10]	1 NO2 Show IR|[11]	1 OMe Show IR|[12]	2 OMe Show IR|[13]	2 SiH3Show IR|[14]
C-Cl	765.76	772.61	771.52	767.23	772.9	767.94
C=C (syn)	1756.54	1757.14	1758.05	1757.14	1755.75	1754.91
C=C (anti)	1706.5	1760.51	1738.87	1670.51	1751.63	1653.84

The results shown above show a mixed agreement with the prediction made using the molecular orbitals seen previously.

Initially the effects of electron withdrawing group CN were investigated. It was surprising to see that the addition of this group to the anti alkene actually had the opposite effect to what was expected and caused the C-Cl bond to become weaker. More surpring still was that the addition of another CN group did have the expected effect and caused the C-Cl bond to become stronger. For this reason the effect of a different electron withdrawing group (NO₂) was used to check if this result was anomalous. The addition of (NO₂) had the expected effect.

The addition of an electron donating group (OMe) caused the C-Cl bond to be weakened as was expected. However when 2 OMe groups were added to the anti alkene the C-Cl bond absorption frequency actually increased. A simple explanation for this is that is likely that resonance would exist between the 2 oxygen atoms causing the electron density on the C-C bond to become reduced, and therefore donation into the C-Cl anti-bonding orbital to become reduced. If this was the case you would expect that the C-O bond would display more double bond character in the disubstituted molecule compared to the monosubstituted molecule. This is indeed found to be the case: C-O (monosubstituted) = 1253.43cm^-1, C-O (disubstituted)= 1254.1cm^-1 and 1264.4cm^-1.

Another electron donating group which does not resonate (SiH₃) was used to further back the theory that it is resonance in the OMe example which causes the anomalous result.

Monosaccharide chemistry: Glycosidation

Introduction

In typical cyclohexane rings bearing no heteroatom, it is well known that a large group such as an OH will take up an equatorial position on the ring to avoid unfavourable 1,3 diaxial interactions. This result is reversed when a heteroatom (such as oxygen) is introduced into the ring due to the anomeric effect. This is because it is possible for a lone pair from the heteroatom to be donated into the sigma * orbital of the C-O bond. This provides a large amount of stabilization which is not possible to when the acetyl group is equatorial because there is no anti periplanar relationship between the lone pair and sigma * orbital, and over rides the diaxial interactions.

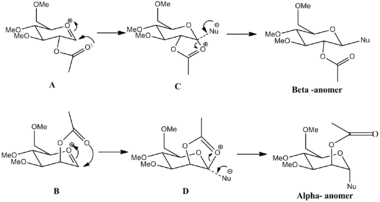
By invoking a neighbouring group effect, with a group such as acetyl is bonded adjacent to the heteroatom, it is possible to selectively produce the Beta-anomer. This is because the acetyl group can quench the oxonium ion by donating a lone pair into the adjacent carbon and eventually forming a bond with it. This new structure blocks the bottom face of the pyranose ring forcing the incoming nucleophile to attack from the top. This produces the Beta anomer. This can be seen in Figure 10 below.

Figure 10 - Dimerisation of Cyclopentadiene

Results and Discussion

Each of the structures above and their ring flipped conformers (A', B', C' and D') had their geometries optimized using MM2 and MOPAC/PM6 calculations and the results are shown below. Although the MM2 calculations were carried it is likely that the structures generated using this method will not be as reliable as the MOPAC/PM6 method because Allinger's MM2 fails to recognise non-classical cations such as the oxonium, and so will not recognise the stabilising interaction between this cation and the lone pairs on the acetyl oxygen. This flaw in the MM2 calculations is a major one in this example. The MOPAC/PM6 calculations on the other hand do take account of these important electrostatic interactions and the effects of this are born out in the geometries and energies produced by each of the methods.

It should also be noted that the choice of R group to be a Methyl was important. Although in a ideal scenario the R group would have been a Hydrogen atom since this is smaller and therefore has the lowest steric demand. The reason a Hydrogen was not used was because this would have created hydroxyl groups on the ring which would have had a larger impact on the energy of the molecule through the formation of new Hydrogen bonds. A methyl group was therefore the next smallest functional group which does not produce these type of interactions.

Table 8 - MM2 energy values of - A, A', B, B', C, C', D and D'

Type of Interaction (kcal mol-1)	Molecule
	A	A'	B	B'	C	C'	D	D'
Stretch	2.34	2.36	2.66	2.41	2.07	2.60	1.99	1.86
Bend	9.82	9.36	10.51	13.48	13.82	16.82	15.24	20.17
Stretch-Bend	0.81	0.88	0.83	0.96	0.73	0.71	0.85	0.73
Torsion	0.97	1.779	0.61	1.78	7.09	6.82	8.86	6.50
Non-1,4 VDW	-1.62	-2.46	0.93	-1.43	-2.50	-2.89	-2.23	-3.22
1,4 VDW	18.97	19.00	18.78	19.00	17.53	19.23	17.93	17.01
Charge/ Dipole	-10.50	-3.31	-24.10	-12.71	-10.2	1.85	-10.98	-5.65
Dipole/Dipole	4.01	4.57	6.79	5.65	8.52	-0.49	-0.85	-2.39
Total MM2 Energy	24.85	32.18	17.03	32.02	28.09	44.29	32.08	35.00

Table 9 - MOPAC (PM6) heat of formation values of - A, A', B, B', C, C', D and D'

Type of Interaction (kcal mol-1)	Molecule
	A	A'	B	B'	C	C'	D	D'
Heat of Formation	-91.65	-67.70	-84.07	-68.23	-91.66	-66.72	-84.07	-66.70

It can be seen from the calculations above that the MM2 and MOPAC/PM6 methods do agree to some extent: in both methods all the ring flipped conformers are less stable than the original conformers. Where they disagree though is the relative stabilities of A and B. In the MM2 method B has a lower energy, whereas using MOPAC A has the lower energy. This difference is due to different parameters used by the MM2and MOPAC methods described above.

It is not surprising that the ring flipped conformers have a higher energy than their parent conformers because the flipping of the ring forces many of the substituents from equatorial to axial, producing unfavourable 1-3 di-axial repulsions. However a closer look at the breakdown of energies given by the MM2 calculations suggest the biggest difference is caused by charge/dipole interactions. The MM2 calculation treats the oxonium ion as a simple oxygen cation with point charge. The charge dipole interaction therefore depends on the distance between the oxygen lone pair on the acetyl and the oxygen cation. These distances can be seen in each of the Jmols: A = 0.418nm, A’=0.422nm, B=0.3nm and B’=0.575nm, there is a good correlation between these distances and the size of the charge dipole interactions.

It can clearly be seen from the MOPAC/ PM6 calculations that the heat of formation for A=C (an -91.6kcal/mol) and B=D (at -84.1 kcal/mol), these values match almost exactly and this clearly illustrates the ability of MOPAC to handle a non classical cation (such as an oxonium) and effectively create new bonds by holding the atoms at the perfect bond distance. This means although the bond is not drawn in for the Aand B molecules the energies produced are the same as C and D respectively. This is very clear when looking at the distances between the oxygen on the acetyl and the carbon next to the cationic oxygen: A= 0.16nm, C=0.16nm, B=0.158nm, D=0.158nm. These short distances in A and B are indicative of a bonding interaction since they are shorter than the typical 0.2nm. These distance in A’ and B’ are 0.341nm and 0.434nm respectively, which is outside the range for a bonding interation and this is the main reason the ring flipped conformers are less stable in the PM6 method.

An alternative way of looking at the above analysis is to use the Jmol diagrams to show the angle of attack of the oxygen lone pair into the carbon. Deviations away from the ideal Burgi-Dunitz trajectory of 107^° for an Sp2 hybridised atom will lead to a higher energy of formation. This is indeed found to be the case: A= 104.7^°, B= 106.1^°, A’= 152.4^°, B’=165.2^°.

The only unexpected result from these calculations is that despite having a shorter O to C distance and more ideal angle of attack isomer B has a higher heat of formations than A, this is most likely due to the acetyl group being on the same face as the largest side chain in the case of B, causing steric repulsions.

Finally, by comparison of the energies of intermediate C/C’ and D/D’ it is clear that the reaction will show strong diastereoselectivty for both of the non ring flipped structures since they are of a far lower energy, especially by MOPAC calculation. These means the reactions pathways shown in the original reaction scheme will be followed exclusively with no ring flipped products.

Mini Project - Regioselective Synthesis of Flavone

Introduction

Flavone is a member of an important class of molecules called γ-benzopyranones which are known to have many biological activities such anti-inflammatory, anti-tumeric and cytotoxic. Below is a highly regioselective synthesis of Flavone proposed by Yoshida, Fujino and Doi in 2011

Figure 11 - ¹³C NMR of Aurone

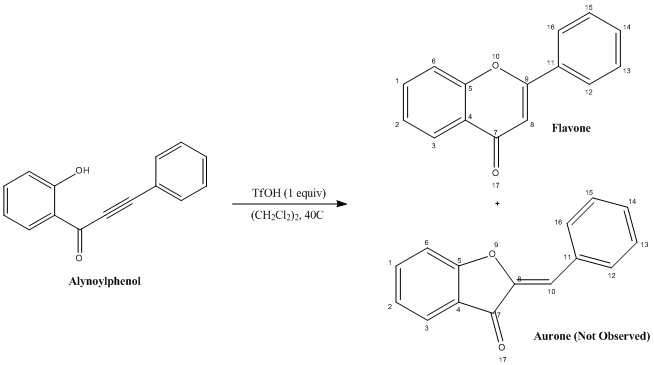
An oxygen lone pair on the hydroxyl group can attack at either side of the alkyne functionality. An 6 endo-digonal cyclization will produce the desired Flavone product, whereas a 5 exo-digonal cyclization will produce the Aurone side product. It is known from Baldwin's rules for ring closure that both of these processes are in fact formally 'favoured'. In this Mini-project computational methods will be used to first explain the selectivity of this reaction and second predict spectra for each of the products to make a comparison with literature in order to test whether computational techniques are accurate enough to support or rule out structures of molecules when the product of a reaction is unknown.

Analysis of Energies

Each of the 3 molecules had their geometries optimized using MM2 and MOPAC/PM6 calculations. The MOPAC/RM1 calculation is also included because it produced a markedly different structure for Aurone, when compared to PM6, with most twisting about the C-C bond attached to the phenyl ring. The MM2 calculations produced flat structures for each of molecules. This can be seen in the Jmol diagrams below.

Table 10 - MM2, MOPAC/PM6 and MOPAC/ RM1 values of Reactant and Products

Type of Interaction (kcal mol-1)	Molecule
	Alkynoylphenol	Aurone	Flavone
Stretch	0.73	1.05	1.37
Bend	2.61	14.21	4.53
Stretch-Bend	0.02	0.04	0.01
Torsion	-9.50	-12.41	-13.61
Non-1,4 VDW	-0.36	-0.06	1.30
1,4 VDW	12.51	14.54	19.42
Dipole/Dipole	-0.71	4.24	1.29
Total MM2 Energy	5.30	21.60	14.30
Total PM6 Heat of Formation	29.58	4.63	-8.96
Total RM1 Heat of Formation	18.31	0.72	-10.85

It can be seen from the calculations above that when using the MM2 parameters the reactant is the most stable molecule and Flavone is the thermodyanamic product. Things change quite dramatically when the MOPAC methods are used (both of which are in general agreement with each other), using semi-empirical calucaltions the Reactant (Alkynoylphenol) is now the least thermodynamically stable molecule. However one thing always remains the same – Flavone is the always the thermodynamic product. Therefore an increase in temperture is likely to cause an incrase in selectivity for Flavone. Within the MM2 breakdown of energies the biggest difference between the 2 products is seen in their bend energies, this is most likely due to the Aurone having slightly more strain since it has a 5 membered ring instead of a 6.

The ideal angle of attack for the hydroxyl oxygen into a sp hybridized centre (i.e. either side of the alkyne functionality) is 120^°. This geometry leads to the optimum overlap between the lone pair orbital and the sigma* sp orbital. It can be seen from the Jmol diagram for Alkynoylphenol (RM1) that the angle of attack to produce Flavone is 104.1^°, compared with 55.3^° for Aurone. This is an extremely large difference and explains why the reaction is so highly selective for Flavone. Similar results are seen in the MM2 and PM6 Jmols but to a lesser extent. As a result it was decided that future optimizations for prediction of spectra would be run in RM1, before being DFT geometry optimized again by SCAN.

¹³C NMR Spectroscopy

The structures for Aurone and Flavone were drawn out in ChemBio 3D and minimized suing MM2 and then MOPAC/RM1, their geometries were then DFT optimised using SCAN. The resulting Formatted Checkpoint File was then resent to SCAN to calculate the NMR spectrum.

Figure 12 - ¹³C NMR of Flavone

Figure 13 - ¹³C NMR of Aurone

Table 11 - ¹³C NMR, Reference = TMS mPW1PW91/6-31G(d,p) CDCl3 GIAO

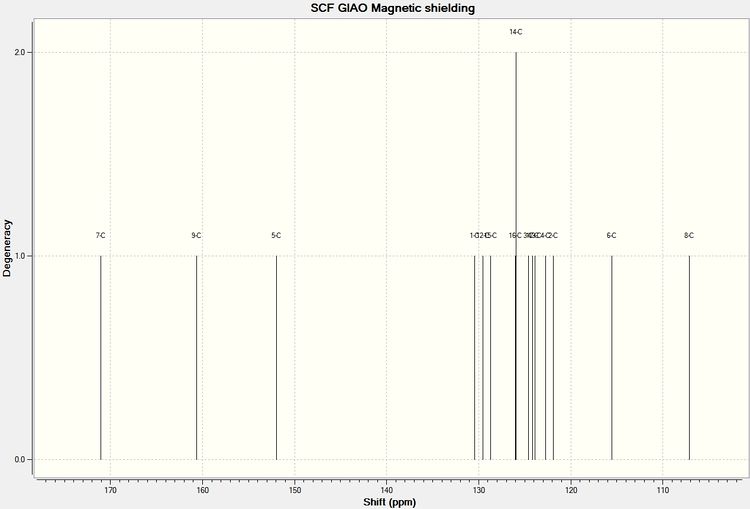
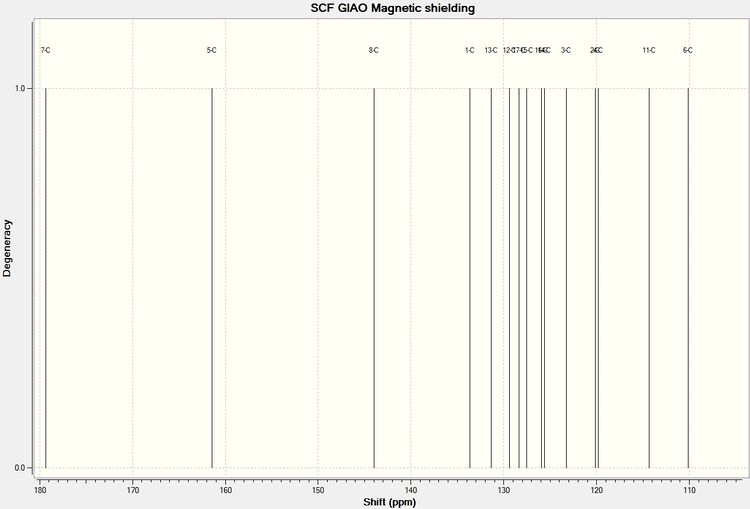
Environment	Aurone			Environment	Flavone
	13C Peak Shift (δ,ppm)				13C Peak Shift (δ,ppm)
	Computationally Predicted	Literature value	Difference		Computationally Predicted	Literature value	Difference
7	179.3	184.7	-5.4	7	171.0	177.9	-6.9
5	161.5	166.0	-4.5	9	160.7	162.9	-2.2
8	144.0	146.8	-2.8	5	152.0	153.8	-1.8
1	133.7	136.8	-3.1	1	130.4	133.4	-3.0
13	131.4	132.2	-0.8	12	129.6	131.3	-1.7
12	129.4	131.5	-2.1	15	128.7	128.7	0.0
17	128.3	129.8	-1.5	16 and 14	126.0	125.9	0.1
15	127.5	128.8	-1.3	3 and 17	124.3	125.2	-0.9
16 and 14	125.7	124.6	1.1	13	123.9	124.8	-0.9
3	123.3	123.4	-0.1	2 and 4	122.3	123.6	-1.3
2 and 4	119.9	121.6	-1.7	6	115.5	117.8	-2.3
11	114.3	113.0	1.3	8	107.1	107.1	0.0
6	110.1	112.9	-2.8	-	-	-	-

It can be seen from the difference column for each of the products that with the exception of shift at the highest ppm for each of the molecules the computational prediction agrees well the literature values, with most values within 2ppm of the literature. The reason for the high discrepancy at low field is unknown.

The carbon environment which shows the biggest difference between each of the product isomers is environment 8 (please refer to reaction scheme to see this carbon in each molecule) for this reason this carbon can be used to characterise which product has been produced in this reaction. In Flavone C8 = 107.1ppm (lit) 107.1ppm (by computational) In Aurone C8 = 146.8ppm (lit) 144.0ppm (by computational)

It can be seen that computational methods predicted these peaks to a satisfactory accuracy and it would be very easy to characterise the molecules since the difference in ppm is 36.9ppm. Since there is no shift in Flavone spectrum expected between 130.4ppm and 152.0ppm (computationally) if a peak was observed in the experimental spectrum for an unknown product of this reaction at around 144-146ppm it would a strong indication that some Aurone is present in the product. Absence of this peak and presence of a shift at around 107ppm would strongly indicate only Flavone has been produced selectively.

IR Spectroscopy

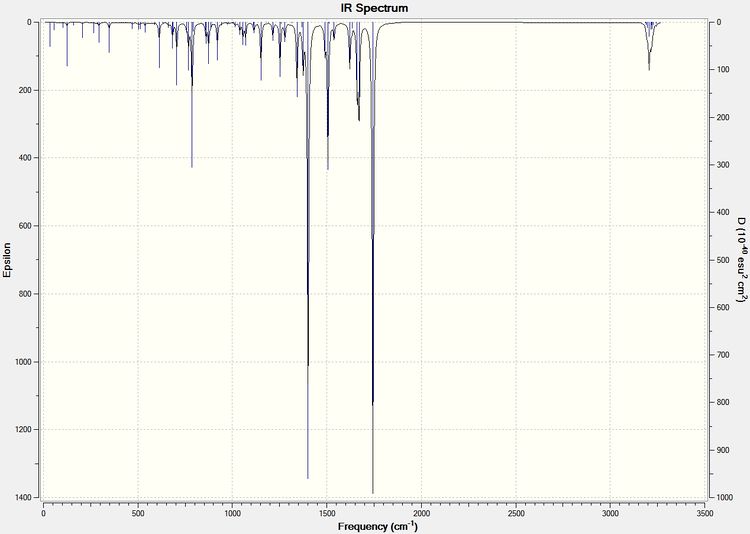
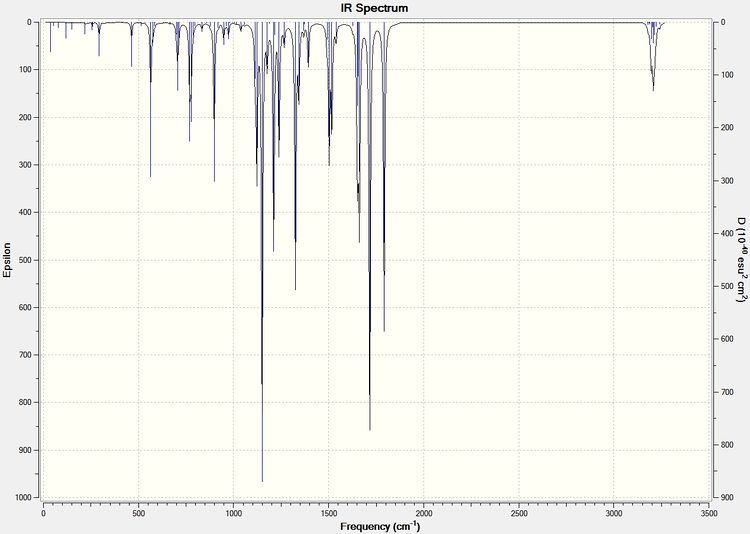
The same procedure to find the NMR spectra were used to calculate the IR spectra.

Figure 14 - IR Spectrum of Flavone

Figure 15 - IR Spectrum of Aurone

Table 12 - Summary of Important Data from the Vibrational Spectra for Aurone and Flavone

Type of Bond Vibration (cm-1)	Molecule
	Aurone	Flavone	Literature Value Aurone	Literature Value Flavone
C=O	1792.10	1743.69	1709	1670
C=C (C8-C10) Aurone and (C9-C8) for Flavone	1716.35	1670.46	1654	1604

It can be seen from the IR spectral data above the C=O bond is stronger (higher frequency) in Aurone, and the C=C bond is also stronger in Aurone.

The reason the C=O bond is weaker in Flavone is because it has an s-trans relationship, this allows the carbonyl moiety to conjugate and form resonance structures with the C=C bond. This is made possible because the orbitals have an anti-periplanar relationship. This type of conjugation is not possible in Aurone because it has an s-cis structure. This means that the electrons are more localized at both C=O and C=C bonds making them stronger and absorb at higher frequency.

With large differences between the absorptions should make the molecules easy to characterise by IR spectroscopy. However it can be seen by comparison to the literature values that the results produced by the computational calculations are not all that accurate, with all absorptions 60-90cm^-1 lower than the literature. They do however show the correct trend with all Flavone absorptions weaker than the Aurone ones.

UV Spectroscopy

The same procedure to find the NMR spectra were used to calculate the UV spectra.

Figure 16 - UV Spectrum of Flavone

Figure 17 - UV Spectrum of Aurone

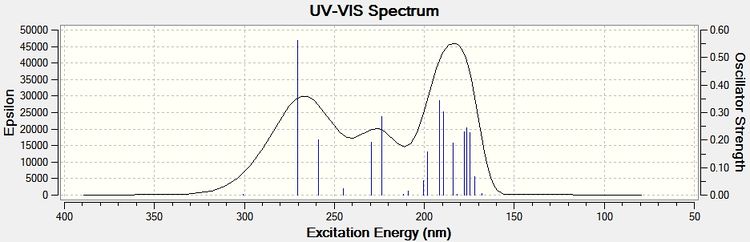
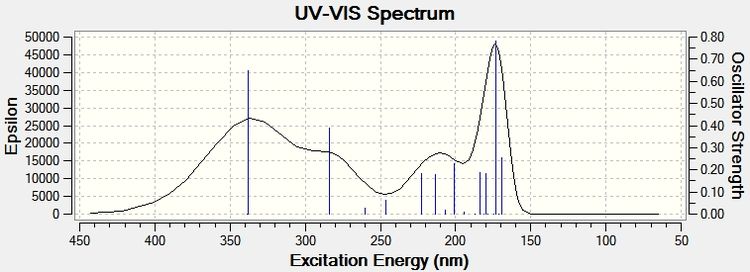
It can be seen from the above UV spectra for each product isomer that their absorptions are quite similar and therefore it would be difficult to characterise isomers from each other using this technique. Agreement with literature is good, literature values could not be found using chloroform solvent, however since benzene is fairly similar solvent (with close dielectric constant) a decent comparison can be made from it. An absorption of 291.002nm (lit) for Flavone shows good agreement with the computational result.

For Aurone the only literature that was found was taken from ethanol (a very different solvent) and only a very general result was given, absorptions were seen from 220-420nm (lit)

A note on Circular Dichromism

Although the CD Spectra for each of the molecules did produce some activity they were not included in the report since the molecules are not chiral the result should have been a flat line with no activity. The reason the computational SCAN suggests that the molecules are chiral is because during its optimization some transient chiral conformations of the product may be formed through rotations, a CD spectrum carried out in the lab would not give these results.

Overall Conclusion

In conclusion it is clear from the results gained in this wiki that Computational calculations are already accurate enough to be useful in the prediction of energies of molecules and therefore their reactivities. It is also evident that as these computational techniques become more sophisticated (from MM2 to MOPAC to Gaussian) there tends to be a higher accuracy in the calculations and more scope for complex analysis. Clearly in a future with more computational power these techniques will become an imperative in every organic report concerned with selectivity of a reaction, hopefully the Mini project has gone some way in illustrating this.