2OC

Introduction

The aptitude and analytical capacity of various computational methods were considered within this study. Each molecule constructed was subjected to both molecular mechnical [MM2] and quantum mechanical [MOPAC] procedures. Whilst the MM2 force field considered only force constants between bonds, MOPAC provided a more advanced quantum mechanical approach that allowed the making or breaking of bonds. Both of these procedures were invoked in order to rationalise the molecular reactivity and stereoselectivity observed within the molecules in question. In the latter half of the investigation, the spectroscopic data of two isomers found within literature were simulated using computational methods. Further analysis of these simulations with respect to literature data, provided a valuable insight into the extensibility of computational chemistry.

Cyclopentadiene dimer

Cyclopentadiene is susceptible to dimerisation, undergoing a Diels-Alder 4πs+2πs cycloaddition, to produce either an endo or exo form. The exergonic ΔG^o component associated with this reaction, reflects the favourable nature of dimerisation. The two π-bonds within one cylopentadiene ring [fixed in the s-cis conformation] react with one π-bond in the second cyclopentadiene ring to a partiallly hydrogenated dimer structure.

Dimerisation of cyclopentadiene

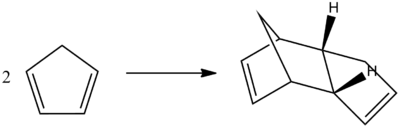
The stereochemistry observed is dictated by the orientation at which a diene and dienophile approach one other. The exo approach defines the substituent on the dienophile directed away from the diene, whereas conversely the substituients on the dienophile are directed towards the endo isomer. In the case of cyclopentadiene the endo is specifically formed.

By considering both the cyclodimerisation process as well as the hydrogentation of cyclopentadiene [to produce a dihydrodervative] one can determine whether such processes are under thermodynamic or kinetic control. Reactions that are under thermodynamic control are reversible, performed at high temperature to yield the most stable product. Under kinetic conditions, reactions are irreversible, favouring the product that has the lowest energy barrier to formation.

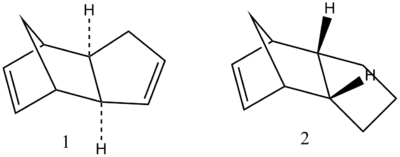
By direct comparison of the exo- [Molecule 1] and endo- [Molecule 2] isomer energies one can determine whether the reaction is under thermodynamic or kinetic control. Using ChemBio3D, the two isomers were constructed and their geometry optimised through the implementation of the MM2 force field.

Exo dimer (above,left); Endo dimer (above,right)

Cyclopentadiene isomers
Energy component
Stretch	1.2859	1.2507
Bend	20.5800	20.8476
Stretch-Bend	-0.8383	-0.8357
Torsion	7.6547	9.5107
Non-1,4 VDW	-1.4157	-1.5428
1,4 VDW	4.2324	4.3194
Dipole/Dipole	0.3775	0.4476
Total Energy [kcal/mol]	31.8765	33.9975

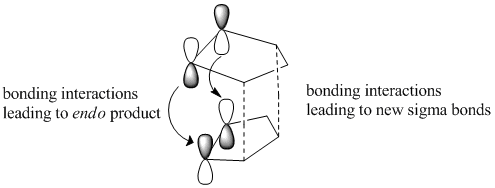
As shown in the table above, the exo- form of the cyclopentadiene dimer has a lower energy [ΔE = 2.121 kcal/mol] than the endo-form and hence is the more stable isomer. Given the predominance of the endo isomer it can be deduced that the reaction is under kinetic control and not thermodynamic control as the more unstable product is formed [endo]. The preferential formation of the endo-product within most kinetic Diels-Alder reactions, or in this case exclusive endo- formation can be rationalised in accordance with Woodward and Hoffman orbital interactions. Woodward and Hoffman emphasized the favorable orbital interactions between the occupied [HOMO] and unoccupied [LUMO] relative to the equivalent interaction observed in the exo-form.

Diagram showing the HOMO-LUMO interactions within the endo-cyclopentadiene dimer

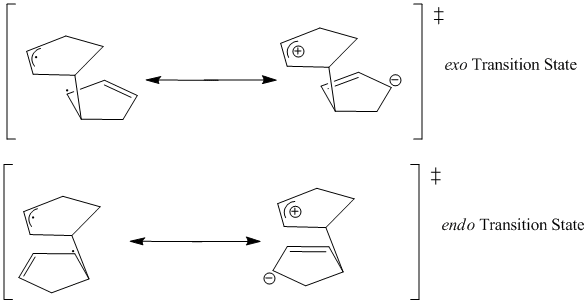
Another hypothesis to explain the selectivity observed, relates to the Diels-Alder transition states . Given the asynchronous nature of the mechanism, the transition state can be depicted using multiple resonance structures. In the case of a zwitterion ion resonance, the proximity of the two charges within the endo form has a stabilising effect.

Exo and Endo transition states within Diels-Alder reaction of two cyclopentadienes

Hydrogenation of cyclopentadiene dimer

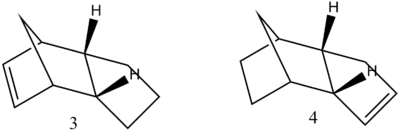
As deduced previously, the endo-isomer is the major product of dimerisation. The partial hydrogenation of this isomer can yield either the dihydro derivative 3 or 4 [shown below]. By comparing the relative energy contributions present within each molecule one can make a thermodynamic prediction regarding the ease of hydrogenation of each double bond in 2 [endo].

Partially hydrogenated dihydro derivatives, 3 (below,left) 4 (below,right)

Cyclopentadiene dihydro derivatives
Energy contribution
Stretch	1.2853	1.1303
Bend	20.5803	13.0161
Stretch-Bend	-0.8380	-0.5650
Torsion	7.6547	12.4119
Non-1,4 VDW	-1.4157	-1.3264
1,4 VDW	4.2323	4.4396
Dipole/Dipole	0.3775	0.1410
Total Energy [kcal/mol]	31.8765	29.2475

As shown above, the derivative 3 has a higher energy than that computed for derivative 4 [ΔE=2.629 kcal/mol]. This observation can be explained with regard to the nature of the double bond present in each molecule. The double bond in derivative 3 is constrained within the cyclopentene ring, adjacent to the bridged carbon. The strain enforced on this double bond is exhibited in the higher torsion observed [20.5803 kcal/mol] relative to the torsion within derivative 3 [13.0161 kcal/mol]. The increased strain of derivative 3 is in accordance with the bond angle observed, 107.6^o, compared to the 112.8^o observed in derivative 4 which is closer to the optimal sp² angle of 120^o. Thus, the hydrogenation of the constrained double bond results in a significantly lowering of the energy in derivative 4 [29.2475 kcal/mol].

Taxol synthetic intermediate

Studies of carbinol chemistry, have led to the observation that specific carbinol substrates have a capacity to undergo atropselective anionic oxy-Cope rearrangements.

oxy-Cope rearrangement to form either atropisomer 9 or 10

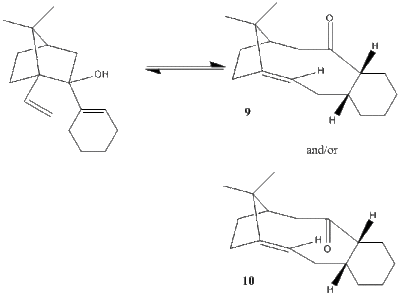
A prominent intermediate in the synthesis of Taxol [shown in the diagram above], can be formed with the carbonyl group either up or down within the ring. This is a form of atropisomer, which can be defined as stereoisomers whereby restricted rotation about a single bond is present and the high steric barrier to rotation allows the isolation of the two conformers. Thus, consideration to the energies of the two atropisomers will provide evidence of their relative stabilities.

Energies of atropisomers using MM2
Energy component
Stretch	2.6356	2.4679
Bend	13.9695	12.3844
Stretch-Bend	0.3507	0.2138
Torsion	20.9810	16.2282
Non-1,4 VDW	-1.5678	-2.0100
1,4 VDW	13.9385	12.4488
Dipole/Dipole	-1.5837	-1.5848
Total Energy [kcal/mol]	48.723	40.1481

Energies of atropisomers using MMFF94
Energy component
Total Energy [kcal/mol]	66.6169	60.0472

As shown above, the MM2 force-field optimisation differentiates the two isomers, showing the larger energy of molecule 9 [with carbonyl facing up], 48.7238 kcal/mol, compared to 40.1481 kcal/mol for molecule 10.

The optimisation calculation was then repeated using a different force-field, in the form of MMFF94. The computed energies are shown in the table below those of the MM2 optimisation. A larger energy, 66.6169 kcal/mol, is again observed for molecule 9 compared to molecule 10,60.0472 kcal/mol.

Furthermore, the stretch and bend energies are lower in isomer 10 than in isomer 9, suggesting greater stability of isomer 10.

Thus, through both optimisation procedures it can be rationalised that molecule 10 [carbonyl group facing down] is the more stable isomer.

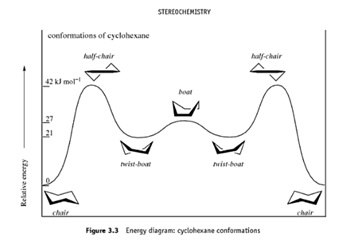
Both optimised forms of isomer 9 and 10 exhibit a chair conformation within the cyclohexane ring; this is the lowest energy conformational form of cyclohexane [see diagram below].

Energy diagram of cyclohexane conformations

A notable feature common to both isomer 9 and 10, is their distinct lack of reactivity. Bredt's rule describes the tendency of alkenes to avoid ring junctions. Yet in the case of isomer 9 and 10 a highly strained bridgehead alkene is present. One might expect such an molecule to be highly reactive, i.e possessing a strong desire to remove this strain, however this is not the case. Olefinic strain (OS) correlates to the stability of a bridgehead olefin, defined as the strained energy experienced by the olefin compared to that of its parent hydrocarbon. Within bridgehead olefins this strain is largely attributed to the twisting around the double bond resulting in a decreased HOMO-LUMO gap, thus they exhibit a highly diradicaloid character. As expected most alkenes exhibit a positive olefinic strain, yet there exists a class of "hyperstable olefins", with negative OS values and as a consequence are less strained than their parent hydrocarbons. This is a fundamental explanation underlying isomer 9 and 10's lack of reactivity. This unreactivity can not be rationalised by steric hindrance or increased π bond strength but due to the intrisnic stability of the caged alkene structure and the notable strain of the parent polycycloalkane.

Regioselective Addition of Dichlorocarbene to a diene

The reaction of dichlorocarbene and 9-chloromethanonapthelene has been reported within literature to exhibit a high level of π-selectivity upon addition of the dichlorocarbene to the unsymmetrical 9-chloromethanonapthelene molecule. The electrophilic addition occurs regiospecifically on the double bond endo to the bridged chlorine atom, this is shown in the diagram below.

Regioselective addition of dichlorocarbene to 9-chloromethanonapthelene (endo-isomer formed)

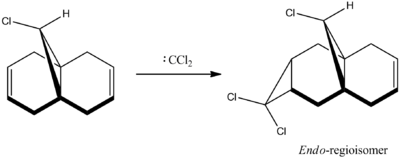
The optimised geometry of 9-chloromethanonapthelene was computed using both the MM2 and MOPAC processes. The output energies for both procedures are shown below.

Energy component	Energy
Dipole/Dipole	0.1123
Total Energy [kcal/mol]	17.8945

Energy component	Energy
Heat of formation [Kcal/Mol]	22.82787

To ensure any discrepancies between the MM2 and MOPAC procedure were accounted for, the two optimised structures were superimposied upon each other, tethered by three pairs of atoms.

Superimposed MM2 and MOPAC optimised structures
Bond pair	Bond distance [Å]
C(1)-C(26)	0.2184
C(2)-C(27)	0.1553
C(1)-C(26)	0.0513

A significant difference is apparent between the two superimposed MM2 and MOPAC structures. Whilst the MM2 method only considers force constants within the optimisation, the quantum mechanical MOPAC method considers through space interactions [i.e electronic distribution] within the molecule. As seen from the superimposed structure there is a strong repulsion between the endo double bond and chlorine atom on the MOPAC structure [the bottom structure as shown]. This repulsion is not observed on the MM2 structure, whilst both structure show good overlap on the exo double bond unaffected by electronic repulsions with the chlorine atom.

The molecular orbitals within 9-chloromethanonapthelene were calculated using Guassian interface and subsequently visualised within ChemBio 3D. The realized molecular orbitals and their respective energies are shown within the table below.

Molecular orbitals
Energy Level	HOMO-1	HOMO	LUMO	LUMO+1	LUMO+2
Molecular orbital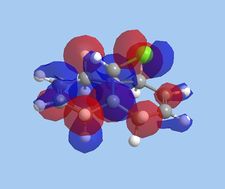
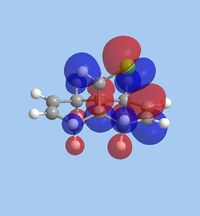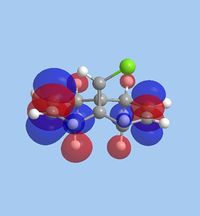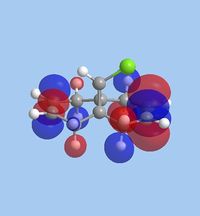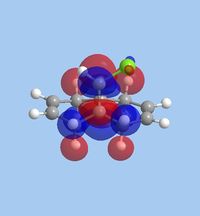
Energy [eV]	-10.9	-10.407	0.966	1.401	15.113

The reactivity observed within this reaction can be attributed to the specific interactions occurring within the HOMO-LUMO region. The most pertinent interaction is that of the HOMO-1 [exo-,electrophilic π bond] and LUMO+2 [C-Cl σ*]. An optimal orbital anti-periplanar alignment is present between these two orbitals,allowing an impulse of electron density into the C-Cl σ* bond increasing the "bonding" nature of the C-Cl σ* bond. . Conversely, this overlap results in an increase in electron density on the exo-π bond, which is pushed into the anti-bonding π* orbitals of the alkene. The endo-π bond more is rendered more nucleophilic with regard to both frontier orbital and electrostatic analysis. The electrostatic potential of 9-chloromethanonapthelene displays a distinct perturbation of electron density, with a greater proportion of density surrounding the nucleophilic endo-π bond compared tor the exo-π bond. This is shown below:

Electrostatic potential observed within 9-chloromethanonapthelene

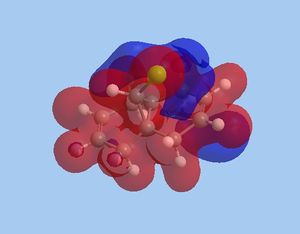
As a consequence of the exo-π/σ*C-Cl interaction , the alkene character of the π bond is reduced [due to electron density within the π* orbitals] and the п bond is weakened. This is in accordance with the frequencies computed, whereby the exo π bond has a lower wavenumber [1737.04cm^-1] compared to the nucleophilic endo π bond [1757.35cm^-1]. With regard to bond distances, the exo alkene bond has a longer bond distance, 1.336Å compared to the endo alkene bond, 1.332Å. This substantiates the more anti-bonding nature of the exo alkene, which increase the C-C bond distance.

Bond distances
C-C exo- bond distance [Å]	1.336
C-C endo- bond distance [Å]	1.332
C-Cl σ* bond distance [Å]	1.789

Frequencies
C-C exo- [cm-1]	1737.04
C-C endo- [cm-1]	1757.35
C-Cl σ* [cm-1]	770.86

Monosaccharide chemistry- Glycosidation mechanism

Glyocisdation is a highly stereospecific reaction where by an X group on a pyran ring is displaced by a nucleophile, Nu. The stereochemistry exhibited by the C-OAc group governs the stereochemical outcome of the attacking nucleophile. The formation of a glycosidic bond and the stereochemical discrepancies are shown in the diagram below [where R=Me].

Schematic showing the stereochemical ambiguity/permutations associated with glcyosidation

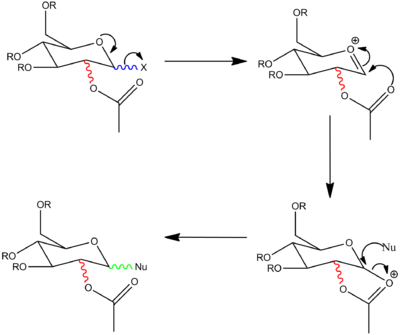
The high degree of stereoselectivity observed is as a direct consequence of neighbouring-group participation, whereby the adjacent acetal group forms an oxonium cation intermediate, which can be displaced by either a nucleophile attacking from the top or bottom face. The top and bottom face correspond to the formation of a β-anomer or α-anomer..

The two possible pyranose conformations each with two associated -OAc orientations within the oxonium cation pyranose molecule were determined and depicted within Chembio3D. The intermediates associated with each of these four conformations were also constructed. The various glycosidation mechanisms observed with each distinct conformation are depicted in the diagram below.

Possible mechanistic routes of glycosidation yielding either alpha/beta 1,2cis/trans products

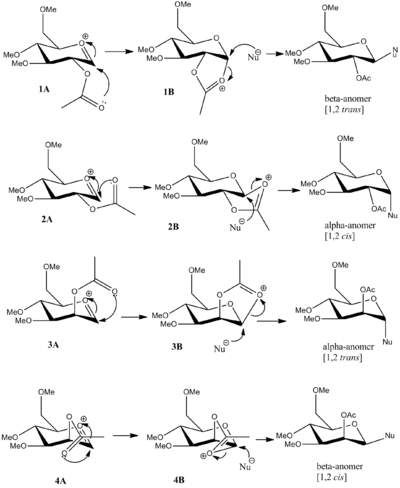
An MM2 force field procedure was undertaken on each molecule to obtain an optimisation energy. The results are shown in the table below.

Comparison of MM2 α-β anomer energies
Component	MM2	MM2	MM2	MM2	MM2	MM2	MM2	MM2
Stretch	2.4185	2.7517	2.4744	2.9170	2.4239	1.9328	2.3649	2.5018
Bend	8.6612	18.9357	8.4630	19.4629	10.0321	17.7750	9.0494	20.1230
Stretch-Bend	0.8247	0.7625	0.8605	0.7470	0.9712	0.6149	0.9105	0.7955
Torsion	3.1363	7.4455	1.7205	5.1269	2.4126	5.6825	2.0298	4.8768
Non-1,4 VDW	-1.1547	-4.1238	-3.2385	-3.1302	-0.2448	-3.7766	-4.1883	-3.3182
1,4 VDW	19.9218	18.8946	19.0296	18.6987	18.8590	17.3395	18.8854	18.2176
Charge/Dipole	-19.0094	2.7319	3.4999	1.8806	-20.6927	3.2619	6.6214	0.4184
Dipole/Dipole	6.1274	-1.7523	3.6726	-0.1004	7.5593	-0.4255	3.6863	0.5952
Total Energy [kcal/mol]	20.9258	42.4044	36.4821	45.6458	21.3206	44.2100	39.3594	45.60254

In the case when the 2 position of the 2-acetylpyranose is occupied by an acetyl group, either below or above the plane of the ring [1A-4A], an intermediate acetoxonium cation can be formed due to neighbouring group participation [1B-4B], stabilised by resonance within the heterocycle ring [1B-4B]. The formation of the acetoxonium intermediate [1B-4B] hinders the nucleophiles access to and overlap with the C-O σ* bond on the intermediate. In the specific case of the cis forming α- and β- anomers [2B and 4B] this inaccessibility within the acetoxonium intermediate [2B and 4B] is very prominent, hence the trans isomers are the principal route observed compared to the cis products.

It is apparent from the table above, that the initial oxonium cations formed [1A-4A] are of a lower energy than the acetoxonium cation intermediates formed within the reaction [1B-4B] following neighbouring group participation [~15 kcal/mol]. This can be rationalised by the conformationally strained nature of the 1B-4B intermediates compared to the 1A-4A intermediates. The calculations above were based on a MM2 force field, which considers only force constants and thus can't form bonds which were not initially inputed. A more advanced MOPAC procedure can be enforced which can consider through space interactions [as well as make or break bonds], using a quantum mechanical approach underpinned by the Schrödinger equation. The results for the MOPAC energies computed are shown in the table below.

MOPAC/PM6 energies of α-β anomers
Energy component	1A	2A	3A	4A	1B	2B	3B	4B
Heat of formation	-89.24	-77.42	-84.07	-68.14	-85.75	-66.84	-67.00	-66.84

As shown in the table above, the MOPAC/PM6 energies computed for the secondary cis pathway [2A and 4A] are higher than the primary trans pathway [1A and 3A]. This is consistent with the energies observed using the MM2 method, whereby 1A and 3A are of lower energy. One can rationalise this energy disparity by considering the proximity of the anomeric carbon and the oxygen on the acetyl oxygen. The distances describing this interaction are shown in the table below.

Distance between anomeric carbon and acetyl oxygen after MM2 and MOPAC/PM6 optimisation
Molecule	1A	2A	3A	4A
MM2 C-O distance [Å]	2.58	2.93	2.56	4.08
MOPAC C-O distance [Å]	1.59	2.76	1.58	3.6683

The MOPAC distances for isomers 1A-4A were all shown to be lower than the respective MM2 distance measurements. The lower MOPAC distances can perhaps be attributed to MOPAC's quantum mechanical approach enabling the breaking and formation of bonds, this can cause cause a greater disruption to the 2-acetylpyranose structure. Hence, placing the acetyl oxygen in close proximity to the anomeric carbon increases the neighbouring group interaction and further reducing the energy of the structure.

The lower bond distances observed in 1A and 3A are consistent with the energies computed using the MM2 and MOPAC/PM6 methods. As shown previously, the energies of 1A and 3A are significantly lower than those observed in 2A and 4A. Given the close proximity of the anomeric carbon and acetyl oxygen in both 1A and 3A a more favourable interaction can occur, thus increasing the neighbouring group participation. Conversely, the larger anomeric cabon/acetyl oxygen separation in 2A and 4A reduces the effect of neighbouring group participation.

Given the SN1 nature of the glycosidsation, one can consider the angle at which the nucleophile attacks the anomeric centre. The Bürgi-Dunitz angle, 107^o, can be defined as the optimum angle of nucleophilic attack. By considering the MOPAC structures of 1A and 3A it can be seen that the angle of nucleophilic attack is 104.4^o and 105.9^o. These angles are close to the ideal Bürgi-Dunitz and thus validate the strong neighbouring group stabilization that is observed within 1A and 3A. Conversely, 2A and 4A have a nucleophilic attack angle of 160.7^o and 153.1^o which is far from the optimum Bürgi-Dunitz angle.

It is evident from the MM2 and MOPAC energies that the 1B and 3B acetoxonium cation intermediates are lower than the 2B and 4B isomers. This can be attributed to the conformationally stable planar 5-membered ring formed, allowing resonance throughout the acetoxonoium ring. In the case of 2B and 4B, a highly conformationally strained intermediate 5-membered ring is formed, reducing the resonance stability within the acetoxonoium ring. The primary pathway in the α and β anomeric formation is consequently the 1,2 trans mechanistic route not the 1,2 cis route, i.e through isomers 1B and 3B.

¹³C NMR Spectra of Taxol synthetic intermediate

As seen in earlier discussions, the energy of two atropisomeric Taxol intermediates were computed and analysed using various compuational methods. For the forthcoming section of the investigation, the lower energy conformer [shown below] was considered. Using computational methods, the ¹³C NMR of this Taxol synthetic intermediate was simulated and compared to that in literature.

Structure of Taxol synthetic intermediate

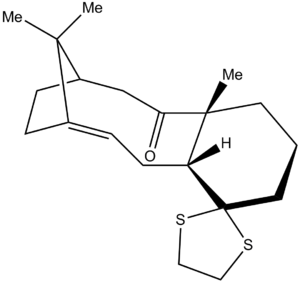
The molecule was initially optimised using the MM2 procedure before minimising using a DFT method [DFT=mpw1pw91], a basis set of 6-31G [with (d,p) polarization] and a CPCM solvation field of benzene . The ¹³C NMR was subsequently computed and analysed with reference to TMS [mPW1PW91/benzene]. The results [shown below] were then assessed in relation to those described in literature [75 MHz, C₆D₆].

Table showing the 13C chemical shift comparison

Bar chart depicting 13C chemical shift comparison between computed and literature

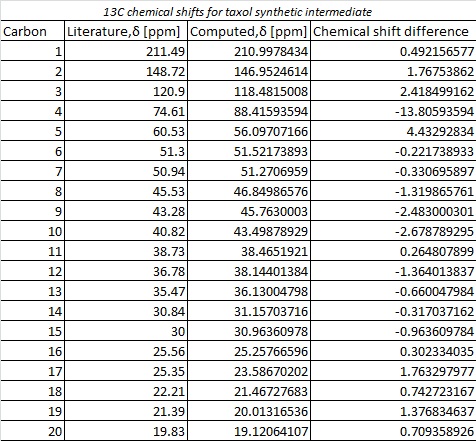
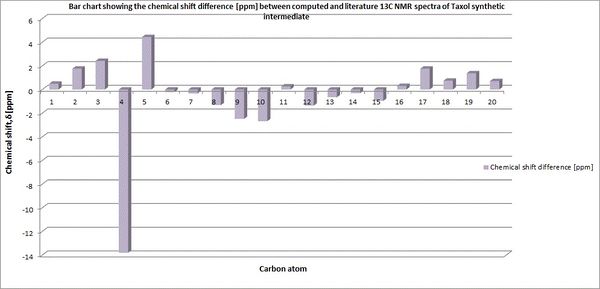
From comparison of the simulated and literature ¹³C, a reasonable correlation is observed between the two. Whilst there are some fluctuations, with the peak at 74.61 ppm within literature observed at 88.41 ppm in the simulation, this can be attributed to spin-orbit coupling as the carbon in question is bonded to heavier atoms i.e the dithiane group. The overall disparity is minimal with all other comparable carbon nuclei in a range of +/- 4ppm. This provides evidence of the power of computational methods in simulating analytical methods, such as ¹³C NMR,within organic molecules.

Regioselective synthesis of benzo[b]furans

A recent research study has established a convergent and regiocontrolled synthesis of 2- or 3-substituted benzo[b] furans using ortho-substituted phenols and α-bromoacetophenones. The 2-selective isomer can be obtained through a one step process using xylene [under reflux] and neutral alumina, whereas one can yield the 3-substituted regioisomer in two consecutive steps [heating with potassium carbonate and acetone, followed by the addition of alumina]. .

The reaction scheme shown below describes the synthetic routes to achieve both the 2 and 3-substituted benzo[b]furan [4,6-Dimethoxy-2-(3,4,5-trimethoxyphenyl)benzofuran and 4,6-Dimethoxy-3-(3,4,5-trimethoxyphenyl)benzofuran respectively].

Reaction scheme describing the one and two steps routes to achieve the 2 and 3-substituted isomers

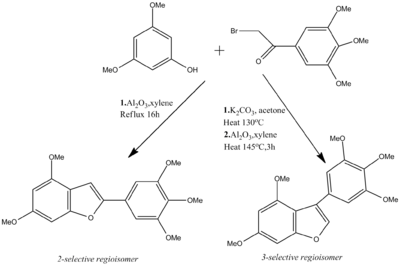
The electronic nature of each R group was seen to have a prominent effect on the reaction. The use of electron-releasing methoxy groups on the starting phenol was seen to have a positive effect on the reaction, whilst the aryl on the α-bromoacetophenone was tolerant to either electron-releasing or electron-withdrawing R groups. In the one step route, no 3-substituted isomer was detected, with a yield recorded of 75% . Derivatives of the 2-substituted product can be used in the synthesis of the natural product of Moracin M.

The 3-substituted isomer was obtained through heating with K₂CO₃ in acetone, initially forming a intermediate ether, which is subsequently dispersed in Al₂O₃. A yield for the 3-substituted isomer was recorded as 50%.

Optimisation of benzo[b]furan isomers

The 2-selective and 3-selective benzo[b]furan regioisomers were constructed using ChemBio3D and were subjected to an initial MM2 optimisation. The results are shown in the table below:

Comparison of MM2 energies
Component
Stretch	2.3222	2.7073
Bend	22.2411	26.3860
Stretch-Bend	0.0050	0.2429
Torsion	-10.0815	-12.5673
Non-1,4 VDW	-1.7156	2.0153
1,4 VDW	26.8910	26.0913
Dipole/Dipole	0.6369	0.7543
Total Energy [kcal/mol]	40.2992	45.6296

Published in D - Space - 2-selective isomer DOI:10042/23297 : 3-selective isomer DOI:10042/23298

These initial geometry optimisation calculations were then refined by using a moire expansive Gaussian optimisation, using a DFT=mpw1pw91 method and a 6-31G(d,p) basis set.

To consider the electrophilic and nucleophilic nature of the components one can examine the synthetic equivalents of both the α-bromoacetophenone and the phenol [shown below].

Schematic showing synthetic equivalents and the convergent synthesis of 2- and 3-substituted Benzo[b]furans

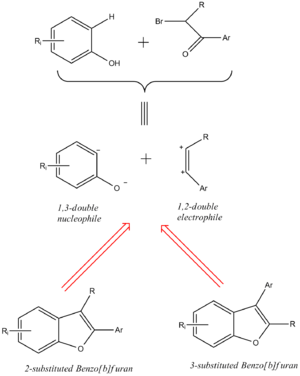
Through the use of computational methods the literature reported that in the absence of alumina, the 3-selective isomer was observed due to an SN2 process between the phenoxide anion [hardest nucleophilic center present] and the electrophilic methylene group adjacent to the bromine atom. The subsequent alkoxy ethers formed underwent cyclization in the presence of alumina to form the final 3-selective product. Conversely, in the initial presence of alumina, a tetrahedral Al₄O₆ cage structure is formed coordinating with the carbonyl oxygen. This increases the electrophilic nature of the carbon [C=O], hence nucleophilic attack occurs at this site, yielding the 2-selective benzo[b]furan.

The selectivity observed can be considered with regard to the behavior of the α-bromoacetophenone in the presence or absence of Al₂O₃. In the case of the 2-selective isomer, the inital reaction with alumina forms a tetrahedral Al₄O₆ cage. The structure is found .

The lower energy computed for the 2-selective isomer suggests that it is more favourable to proceed via this tetrahedral alumina cage, than for the 3-selective isomer. Hence, the exclusive 2-selectivity in the one step alumina reaction.

¹³C NMR analysis of benzo[b]furan regioisomers

Having subjected both isomers to optimisation procedures, the log file of each isomers was altered in order to predict ¹³C NMR using a GIAO approach. Using the same DFT method and basis the key words NMR scrf(cpcm,solvent=chloroform) were invoked. It should be noted that the ¹³C NMR recorded in literature was undertaken in CDCl₃ hence the use of chloroform as a solvent in the calculation.

The ¹³C NMR was subsequently computed and analysed with reference to TMS mPW1PW91/6-31G(d,p) CDCl₃ GIAO. The results [shown below] were then assessed in relation to those described in literature [126 MHz, CDCl₃]. The assigned carbons have been displayed on each isomer.

Published in D - Space - 2-selective isomer DOI:10042/23299 : 3-selective isomer DOI:10042/23300

Assignment of ¹³C environments within 2 and 3-selective isomers

Table showing the ¹³C chemical shift comparison between the 2 and 3-substituted benzo[b] furan regioisomers

Bar chart showing the ¹³C chemical shift comparison between the 2 and 3-substituted benzo[b] furan regioisomers

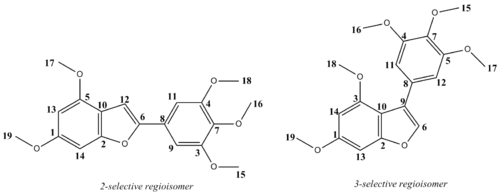
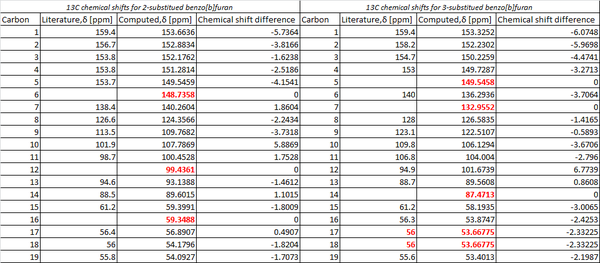
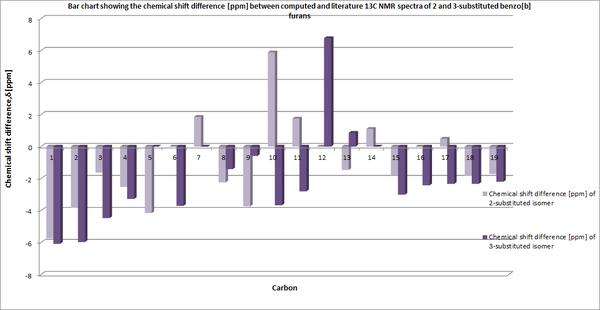
In analysing the computed values with those of reported in literature, significant discrepancies become apparent. Although a relatively small ppm range of +/-7 is observed, given the 19 carbon atoms within each regioisomer one would expect 19 carbon shifts to have been stated in literature. Yet, in the case of both regioisomers fewer carbon shifts are reported. In the 2-substituted isomer, 16 peaks were reported and within the 3-substituted isomer only 15 peaks were reported. This apparent absence of peaks within literature can perhaps be attributed to the carbon shifts being grouped together within literature [i.e one shift value corresponding to more than one carbon]. Furthermore, the diminished intensity of chemical shifts due to quaternary carbons may have resulted in unobserved or at least undistinguishable peaks within the experimental ¹³C NMR spectra.

The shift of aryl group between the 2 and 3- should in theory enable one to distinguish between the environment each carbon is exposed to. For the 3-substituted isomer, carbon 6 bonds to a hydrogen whilst carbon 9 is bonded to the aryl group. Both carbons show very similar chemical shifts to those found in literature [Lit/Comp:140/136:123/122]. One would expect this method could be used in the 2-substituted isomer, however the corresponding carbons [12 and 6] have no directly comparable literature value. Thus, it is not possible to compare the chemical shifts with literature values.

¹H NMR analysis of regioisomer

Having considered the ¹³C NMR the optimised log file of each isomers was altered in order to predict ¹H NMR using a GIAO approach.

The ¹H NMR was subsequently computed and analysed with reference to TMS mPW1PW91/6-31G(d,p) CDCl₃ GIAO. The results [shown below] were then assessed in relation to those described in literature [500 MHz, CDCl₃]. The assigned carbons have been displayed on each isomer.

Assignment of ¹H environments within 2 and 3-selective isomers

Table showing the ¹H chemical shift comparison between the 2 and 3-substituted benzo[b] furan regioisomers

Bar chart showing the ¹H chemical shift comparison between the 2 and 3-substituted benzo[b] furan regioisomers

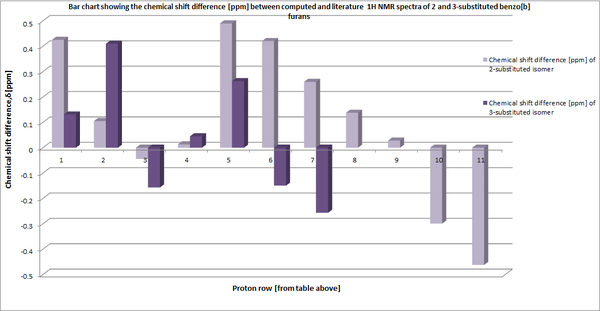
In contrast to the ¹³C chemical shifts,the computed 1H NMR shows a greater correlation with that of literature. It can be seen from the table above that all 20 hydrogens within the benzo[b]furan are accounted for in both the 2 and 3-selective regioisomers. However, there is a minor discrepancy between the number of chemical shift values and their respective integral which must be considered. In the case of the 2-substituted regioisomer, the literature shifts,3.95ppm,3.91ppm and 3.89ppm [highlighted in red above] have been assigned with an integral of 3H each. Whereas, the simulation assigns 6 distinct chemical shift values within a range of 4.44-3.4ppm (excluding the peak at 3.97ppm), with an assigned integral of 1H,2H,2H,1H,2H,1H. One can infer from this observation that within literature these 6 peaks have most likely been grouped together into 3 peaks with an integral of 3H each. The peak recorded in literature at 3.97 has an integral of 6H, which is comparable to the computed NMR peak at 3.67 with an identical integral. Using the simulated ¹H NMR values within GaussView, these peaks can be attributed to 6 protons within the three methoxy rings on the 2-selective isomer.

With consideration to the 3-selective isomer, a strong correlation is observed between the literature and simulated ¹H chemical shifts. Although the shifts at 3.87ppm and 3.84ppm [shown in red above] have an integral of 3H each as opposed to 4H [at 4.1 ppm] and 2H [at 3.6 ppm] within the simulated model; this can again be attributed to a grouping effect within the experimental NMR whereby the integrals are shown as 3H and 3H not 4H and 2H.

The chemical shift computed at 3.75ppm with an integral of 9H is in accordance with the literature peak at 3.9ppm [integral 9H]. Using the simulated 1H NMR values within Gaussview, these 9 protons can be assigned to protons present within the five methoxy groups, -OMe, within the 3-substituted isomer.

Whilst the ¹³C NMR comparison proved inconclusive, the ¹H NMR analysis has been rationalised with regard to both the 2 and 3-regioselctive isomer. The number of peaks and their respective integrals can be used to successfully distinguish between the two isomers. The 2-selective isomer has 11 peaks compared to the 7 observed within the 3-selective regioisomer. In addition, the 6H integrated peak is absent in the 3-regioisomer, instead a 9H integrated peak is present.

Vibrational analysis of benzo[b]furans

Having assessed both the ¹H and ¹³C spectra of the two isomers,vibrational analysis was then undertaken. Using a method of B3LYP and a basis set of 6-31G (d,p), the vibrational modes of both isomers were computed. By considering the vibrational output files for both molecules it is clear that there are no negative frequencies, this indicates that a fully optimised geometry was obtained and not a transition state.

Published in D - Space - 2-selective isomer DOI:10042/23301 : 3-selective isomer DOI:10042/23302

2-selective isomer frequencies:

Low frequencies ---   -7.0489   -1.9496    0.0003    0.0007    0.0009    1.1505
Low frequencies ---    9.9844   32.4624   44.0599

3-selective isomer frequencies:

Low frequencies ---   -9.4022   -3.9156   -0.0010   -0.0009   -0.0004    1.8995
 Low frequencies ---   23.7733   32.4480   34.6299

The vibrational output files also yield information regarding the free energy of the molecules [ΔG=ΔH-TΔS]. This is shown in the table below.

Comparison of free energies
Molecule	Free energy [Hartrees]	Free energy [kcal/mol]
2-selective isomer	-1187.066195	-744884.0373625
3-selective isomer	-1187.061630	-744881.172825

The lower free energy of the 2-selective isomer suggests a slightly more stable structure compared to that of the 3-selective isomer.

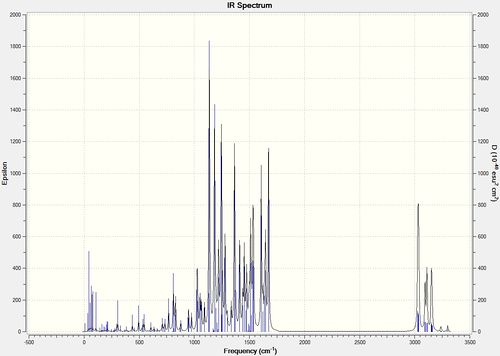
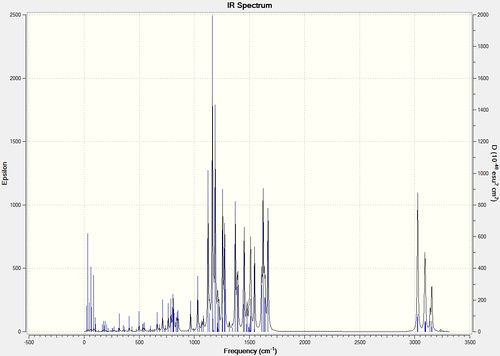
The IR spectrum of each molecule was simulated using the vibrational log file and compared to the IR frequencies recorded in literature.

Comparison of computed and literature frequencies
2-selective literature frequencies [cm-1]	2-selective computed frequencies [cm-1]	3-selective literature frequencies [cm-1]	3-selective computed frequencies [cm-1]
2960	3027.49	2934	3028.07
1619	1622.20	1580	1546.84
1497	1498.99	1414	1453
1227	1244.56	1215	1189
1203	1183.43	1150	1165
1134	1136.68	1120	1125.15

The vibrational frequencies computed are consistent with those reported in literature, with only minor deviations observed. It should be noted, that although 129 vibrations were computed for both isomers, only those of a significant intensity and comparable to those in literature were recorded [6 IR frequencies for each isomer]. Although the two IR spectra computed show strong similarities, the 2-selective isomers are at a slightly higher frequency compared to the 3-selective isomer. This discrepancy is also evident within the literature IR values, thus the isomers can be distinguished due to the higher IR frequencies of the 2-selective isomer.

The two IR spectra below display all the vibrational frequencies at their respective frequencies:

Infra-red spectrum of the 2-selective isomer

Infra-red spectrum of the 3-selective isomer

Conclusion

Computational methods can be invoked to accurately simulate spectroscopic data for a unique molecule. Within this investigation a literature report on the synthetics of two benzofuran regioisomers was considered with regard to computational methods. Using the same starting materials, a unique one step and two step synthetic method was reported to generate the 2 and 3-selective benzofuran respectively. The two isomers were initially optimised before being subjected subjected to ¹³C and ¹H spectroscopic analysis. The computed ¹³C yielded valuable information about the molecular environments present within the compound whilst revealing limitations within the reported literature ¹³C values. Despite the 19 carbon peaks computed within each isomer [C₁₉H₂₀O₆], fewer chemical shifts were reported within literature and thus attempts to differentiate between the two isomers proved inconclusive. The subsequent ¹H NMR analysis proved to be a more powerful tool in distinguishing between the isomers and a better correlation with literature values was realized. Further spectroscopic properties were investigated using vibrational analysis, producing simulated IR spectra. Differences in magnitude of the 2-selective and 3-selctive isomers enabled the distinction between the two isomers. This exercise has highlighted the technical prowess of synthetic chemistry in yielding [separately] a 2 and 3-selective isomer; as well as showing the analytical capacity of computational methods.