200251
IMM2 wiki report - Catherine E Johnson
NH3 molecule
- General Information
ammonia molecule |
Image above shows the structure of the NH3 molecule.
Molecule: NH3
Calculation method: RB3LYP
Basis set: 6-31G(d,p)
Final energy E(RB3LYP): -56.55664124 a.u.
RMS gradient: 0.05399560 a.u.
Point group: C3v
Optimised N-H bond distance: 1.30000
Optimised H-N-H bond angle: 109.471
Item Value Threshold Converged?
Maximum Force 0.000004 0.000450 YES
RMS Force 0.000004 0.000300 YES
Maximum Displacement 0.000072 0.001800 YES
RMS Displacement 0.000035 0.001200 YES
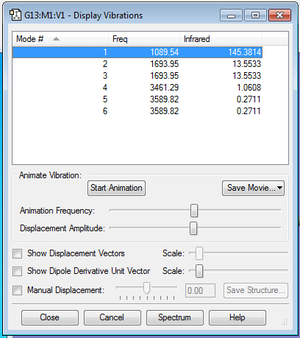
As the NH3 molecule is non-linear, the 3N-6 rule is used to determine the number of modes. The number of modes expected is 6 as N is the number of atoms, which is 4 in this case. As shown in the above image, modes 2 and 3 are degenerate, and so are modes 5 and 6. Modes 1, 2 and 3 are "bending" vibrations and modes 4, 5 and 6 are "bond stretch" vibrations. The most symmetric mode is mode 4. Mode 1 is the one known as the "umbrella" mode. 2 bands should be expected in an experimental spectrum of gaseous ammonia.
Charge on N atom: -1.125
Charge on H atom: 0.375
A negative charge should be expected for the nitrogen atom and positive charges for the hydrogen atoms due to the stronger electronegativity of the N atom.
- H2 molecule
Molecule: H2
Calculation method: RB3LYP
Basis set: 6-31G(d,p)
Final energy E(RB3LYP): -1.17853936 a.u.
RMS gradient: 0.09719500 a.u.
Point group: D∞h
Item Value Threshold Converged?
Maximum Force 0.000000 0.000450 YES
RMS Force 0.000000 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000001 0.001200 YES
The frequency for the vibration of the Hydrogen molecule is 4465.68 cm-1
- N2 molecule
Molecule: N2
Calculation method: RB3LYP
Basis set: 6-31G(d,p)
Final energy E(RB3LYP): -109.52359111 a.u.
RMS gradient: 0.02473091 a.u.
Point group: D∞h
Item Value Threshold Converged?
Maximum Force 0.000001 0.000450 YES
RMS Force 0.000001 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000000 0.001200 YES
The frequency for the vibration of the nitrogen molecule is 2457.33 cm-1
- Reaction Energies
E(NH3)= -56.55664124au
2*E(NH3)= -113.1132824au
E(N2)= -109.52359111au
E(H2)= -1.17853936au
3*E(H2)= -3.53561808au
ΔE=2*E(NH3)-[E(N2)+3*E(H2)]= -0.05407321au = -141.969212855 kJ/mol
Therefore, ammonia, which requires less energy to form, is more stable than hydrogen and nitrogen.
SiH4 molecule
- General Information
silane molecule |
Image above shows the structure of the SiH4 molecule.
Molecule: SiH4
Calculation method: RB3LYP
Basis set: 6-31G(d,p)
Final energy E(RB3LYP): -291.88802760 a.u.
RMS gradient: 0.00000002 a.u.
Point group: TD
Optimised Si-H bond distance: 1.48485
Optimised Si-N-Si bond angle: 109.471
Charge on Si atom: 0.629
Charge on H atom: -0.157
Item Value Threshold Converged?
Maximum Force 0.000000 0.000450 YES
RMS Force 0.000000 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000000 0.001200 YES
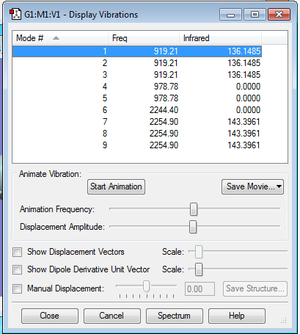
As the SiH4 molecule is non-linear, the 3N-6 rule is used to determine the number of modes. The number of modes expected is 3*5-6=9. As shown in the above image, modes 1, 2 and 3 are degenerate; modes 4 and 5 have the same frequencies; modes 6, 7, 8, and 9 are degenerate as well. Modes 1, 2 and 3 and 4 and 5 are "bending" vibrations and modes 6, 7, 8, and 9 are "bond stretch" vibrations. The most symmetric modes are modes 6, 7, 8, and 9. Modes 1, 2 and 3 are the ones known as the "umbrella" mode. 2 bands should be expected in an experimental spectrum of gaseous ammonia.
- Molecular Orbitals
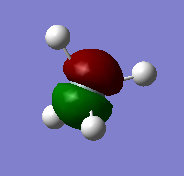
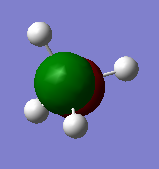
The images above show the 2p atomic orbitals in silicon. They do not contribute to the molecular orbitals in silane.

The image above shows the bonding MO which is contributed by the 1s atomic orbital in hydrogen and the 3s atomic orbital in silicon. It is occupied with 2 electrons and a sigma bond is formed.



The images above show the bonding MOs which are contributed by the 1s atomic orbitals in the hydrogen atoms and the 3p atomic orbitals in silicon. Each orbital is occupied with two electrons.



The images above show the antibonding MOs which are contributed by the 1s atomic orbitals in the hydrogen atoms and the 3p atomic orbitals in silicon. No electrons occupy the orbitals.
