01359003
Ammonia
Molecule Details
Molecule: NH3
Calculation Method: RB3LYP
Basis Set: 6-31G(d,p)
Final Energy (a.u): -56.55776873
RMS Gradient Norm (a.u): 0.00000485
Point Group: C3v
N-H Bond Length (Angstrom): 1.01798
H-N-H Bond Angle (degrees): 105.741
N-H-H Bond Angle (degrees): 37.129
Item Value Threshold Converged?
Maximum Force 0.000004 0.000450 YES
RMS Force 0.000004 0.000300 YES
Maximum Displacement 0.000072 0.001800 YES
RMS Displacement 0.000035 0.001200 YES
Predicted change in Energy=-5.986298D-10
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.018 -DE/DX = 0.0 !
! R2 R(1,3) 1.018 -DE/DX = 0.0 !
! R3 R(1,4) 1.018 -DE/DX = 0.0 !
! A1 A(2,1,3) 105.7412 -DE/DX = 0.0 !
! A2 A(2,1,4) 105.7412 -DE/DX = 0.0 !
! A3 A(3,1,4) 105.7412 -DE/DX = 0.0 !
! D1 D(2,1,4,3) -111.8571 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
Ammonia |
Summary of Vibrational Modes
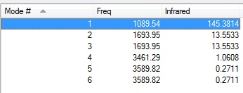
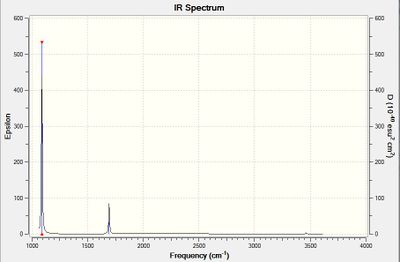
From the 3N-6 Rule, 6 Vibrational Modes are predicted.
From the table, it can be seen that Vibrations 2 and 3, and 5 and 6, are degenerate.
Vibrations 1, 2 and 3 are Bends, given that they have lower vibrational frequencies.
Vibrations 4, 5 and 6 are Stretches, with higher vibrational frequencies.
Vibration 4 is highly symmetric, with the stretching resulting in no change of dipole moment.
Vibration 1 is known as the 'Umbrella Mode' given its remarkable similarity to opening and closing an umbrella.
For a peak to appear in the IR Spectrum, a change in dipole moment caused by the vibration of the molecule is needed. The intensity of the absorption depends on the magnitude of dipole change. Therefore, 4 bands would be expected in an IR Spectrum of gaseous Ammonia, due to the presence of 4 non-degenerate vibrational modes. However, in reality, only two peaks are visible - Vibration 1 and the degenerate Vibrations 2 and 3. The other vibrations have intensities that are too small to be visible, as they do not induce a sufficiently large change in dipole moment to be visible on the spectrum. Vibration 1 is the most intense as it is the stretch which induces the largest change in dipole, hence why the area under the peak for this stretch is the largest.
Charges on Atoms
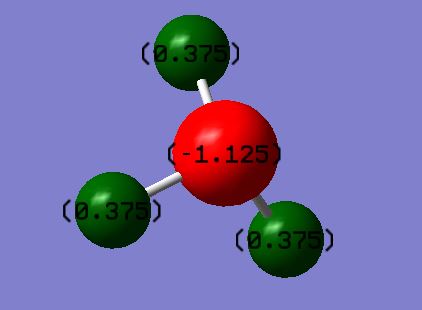
The charges of N and H respectively are -1.125 and 0.375. This fits with current theory as N is a more electronegative element, therefore would take a greater share of the electron cloud, making it negative and H positive.
N2
Molecule Details
Molecule: N2
Calculation Method: RB3LYP
Basis Set: 6-31G(d,p)
Final Energy (a.u): -109.52412868
RMS Gradient Norm (a.u): 0.00000060
Point Group: D*H
N-N Bond Length (Angstrom): 1.10550
N-N Bond Angle (degrees): 180
Item Value Threshold Converged?
Maximum Force 0.000001 0.000450 YES
RMS Force 0.000001 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000000 0.001200 YES
Predicted change in Energy=-3.400967D-13
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.1055 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
Diatomic Nitrogen |
Summary of Vibrational Modes
N2 is a linear molecule and therefore has 3N-5 Modes of Vibration, which works out to one; a symmetric stretch. This stretch is at high frequency due to the strength of the N-N triple bond and the relatively small molar mass of each Nitrogen. However, this vibration does not induce a change in dipole moment, given that both atoms are identical, hence there is no peak present on the IR spectrum.
Charges on Atoms

Given that N2 is a homonuclear diatomic molecule, the charge distribution is equal, there is no dipole moment and the molecule is neutral.
N2 Molecular Orbitals
Molecules appear in order of increasing energy, and are labelled according to the order in which they appear in Gaussview
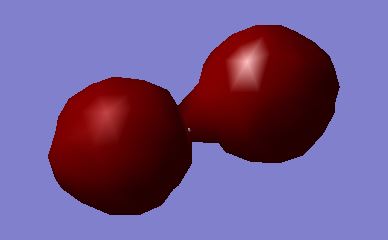
MO1: 1σg Orbital; too low in energy to contribute to the bonding, formed from constructive overlap of the 1s orbitals.
MO2: 1σ*u Orbital - made from out-of-phase overlap of of the 1s orbitals.

MO3: 2σg Orbital, made from constructive overlap of the 2s orbitals.

MO4: 2σ*u Orbital, constructed by out-of-phase combination of the 2s orbitals.

MO5 and MO6: 2πu Orbitals, both degenerate, made from constructive overlap of the 2pz and 2py atomic orbitals.
MO7: 3σg Orbital, made from constructive overlap of the two 2px orbitals.

MO8 and MO9: 2π*g, degenerate orbitals, made from destructive overlap of the 2pz and 2py atomic orbitals.

MO10: 3σ*u Orbital, made from destructive overlap of the 2px orbitals.
The HOMO is the 3σg Orbital, and the LUMO is one of the degenerate 2π*g Orbitals (2pz or 2py. Since the sum of molecular orbitals equals the sum of the atomic orbitals that went in to creating them , there is also an unfilled 3σ*u orbital, which is the highest in energy
H2
Molecule Details
Molecule: H2
Calculation Method: RB3LYP
Basis Set: 6-31G(d,p)
Final Energy (a.u): -1.17853936
RMS Gradient Norm (a.u): 0.00000017
Point Group: D*H
H-H Bond Length (Angstrom): 0.74279
H-H Bond Angle (degrees): 180
Item Value Threshold Converged?
Maximum Force 0.000000 0.000450 YES
RMS Force 0.000000 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000001 0.001200 YES
Predicted change in Energy=-1.164080D-13
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 0.7428 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
Diatomic Hydrogen |
Summary of Vibrational Modes
H2 is also a linear molecule and exhibits 1 vibrational mode - a stretch. It vibrates at very high frequencies due to the extremely low masses of both hydrogen atoms, however, given that it is a homonuclear diatomic, this stretch does not change the dipole moment, and therefore the molecule is IR inactive.

Again, H2 is a homonuclear covalent diatomic, so both atoms are uncharged.
The Haber Process
E(NH3) = -56.55776873 a.u
2E(NH3) = -113.1155375 a.u
E(N2) = -109.52412868 a.u
E(H2) = -1.17853936 a.u
3E(H2) = -3.53561808 a.u
2E(NH3)-[E(N2) + 3E(H2)] = -0.05579074 a.u
The change in energy is -146.48 kJMol-1
Given that this change is exothermic, energy is given out during the reaction, therefore the ammonia product is more stable than the gaseous reactants.
A literature value for the enthalpy of the Haber Process is -92kJMol-1[1]. One reason for this could be that the Haber Process is conducted under extremely high temperatures and pressures in order to achieve an optimal compromise between ammonia yield and reaction rate. The position of equilibrium in industry is shifted over towards the products. The computed value is more exothermic than the industry value, and this disparity signifies that in reality, less energy is released in the reaction than a computational approach would predict.
Cl2
Molecule Details
Molecule: Cl2
Calculation Method: RB3LYP
Basis Set: 6-31G(d,p)
Final Energy (a.u): -920.34987886
RMS Gradient Norm (a.u): 0.00002511
Point Group: D*h
Cl-Cl Bond Length (Angstrom): 2.04174
Cl-Cl Bond Angle (degrees): 180 (Molecule is Linear)
Demonstrating Optimisation
As can be seen in the 'Item' Table Below, the forces and displacements are converged, which means that when there is an infinitesimally small change in the position of the atoms, there is no energy change. It can therefore be concluded that the molecule has been optimised. The final file of the optimisation can be accessed by using the link below.
Media:JPOWELLCL2OPTFPOP.LOG
Item Value Threshold Converged?
Maximum Force 0.000043 0.000450 YES
RMS Force 0.000043 0.000300 YES
Maximum Displacement 0.000121 0.001800 YES
RMS Displacement 0.000172 0.001200 YES
Predicted change in Energy=-5.277376D-09
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 2.0417 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad
Interactive Molecule Diagram
Diatomic Chlorine |
Summary of Vibrational Modes
Cl2 is a linear molecule and therefore has 3N-5 modes of Vibration, which works out to just one: a symmetric stretch.
Vibrational Frequency is proportional to (k)1/2 and to (1/μ)1/2. Therefore, the stretch is at a low frequency due to the fact that each Cl atom is relatively large and the bonding between them is weak, just a single bond. This stretch is invisible on the IR spectrum given that it does not induce a change in dipole moment.
Charge Distribution
Cl2 is a homonuclear diatomic molecule, therefore both atoms are of the same charge given that they have the same electronegativity. The electron cloud is shared equally between the two nuclei.
Cl2 Molecular Orbitals
Molecular Orbitals appear in decreasing order of energy, and are labelled according to how they appear on Gaussview.

MO18: This Molecular Orbital is the LUMO and is made from the linear combination of 3p orbitals. It is a σ*u, and is in fact the only unoccupied antibonding orbital created in diatomic chlorine. It is relatively high in energy.

MO17 and MO16: This Molecular Orbital is the HOMO and is created from the linear combination of 3p orbitals in Chlorine. It is relatively high in energy, and is a π*g orbital. It would act as the lone pair in a nucleophilic attack initiated by the chlorine. There are two of these orbitals, identical to each other in every respect except spatial orientation.

MO15 and MO 14: The πu orbital - this is quite low in energy and contributes to the bonding. It is made from the linear combination of the 3p orbitals. There are two of these degenerate orbitals.

MO13: This σg orbital is made from the linear combination of the 3p orbitals.

MO12: Made from the linear combination of the 3s orbitals in Chlorine, this orbital is σ*u.
Bonding orbitals contribute to the strength of the bonding interactions, whilst antibonding orbitals are destabilising. N2 has a greater ratio of stabilising to destabilising interactions than Cl2, which contributes to the effect observed and corroborated by VSEPR theory of the presence of a triple bond in N2 and a single bond in Cl2.
Chlorine features no interaction between MOs which have the same parity labels, therefore there is no s-p mixing and thus the order of the energies of the Molecular Orbitals is as expected, unlike in N2, in which the πu orbital is lower in energy than the σg orbital. The gap between s and p orbital is larger in Cl2 than in N2, which explains the lack of this mixing.
The net result of less s-p mixing in Cl2 is an effect on the shape of the orbitals, which can be seen when they are compared to those of N2. Cl2 s orbitals have more s character, and all of the p orbitals in the diagrams above contain predominantly p character, which is evident due to their increased symmetrical nature.
Gaussview uses the basis set 6-31G(d,p), which gives all non-Hydrogen s-orbitals slight p character, yielding more flexibility for description of orbitals with greater nodality if needed. This explains the effect described above, and its impact on the shape of the molecular orbitals generated.
Bibilography and References
1. The Haber Process, https://www.chemguide.co.uk/physical/equilibria/haber.html, accessed 09/03/18
Software used for molecular optimisation and generation of MOs was Gaussview