01345038-WikiReport
NH3 Molecule
Running an optimization
NH3
Calculation method- RB3LYP
Basis set- 6-31G(d,p)
Final energy (au)- -56.55776873
RMS gradient- 0.00000485
Point group- C3V
N-H Bond length- 1.01798 angstroms
H-N-H bond angle- 105.741 degrees
Item Value Threshold Converged? Maximum Force 0.000004 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000072 0.001800 YES RMS Displacement 0.000035 0.001200 YES
Viewing an Optimization
NH3 Molecule |
The optimisation file is liked to here
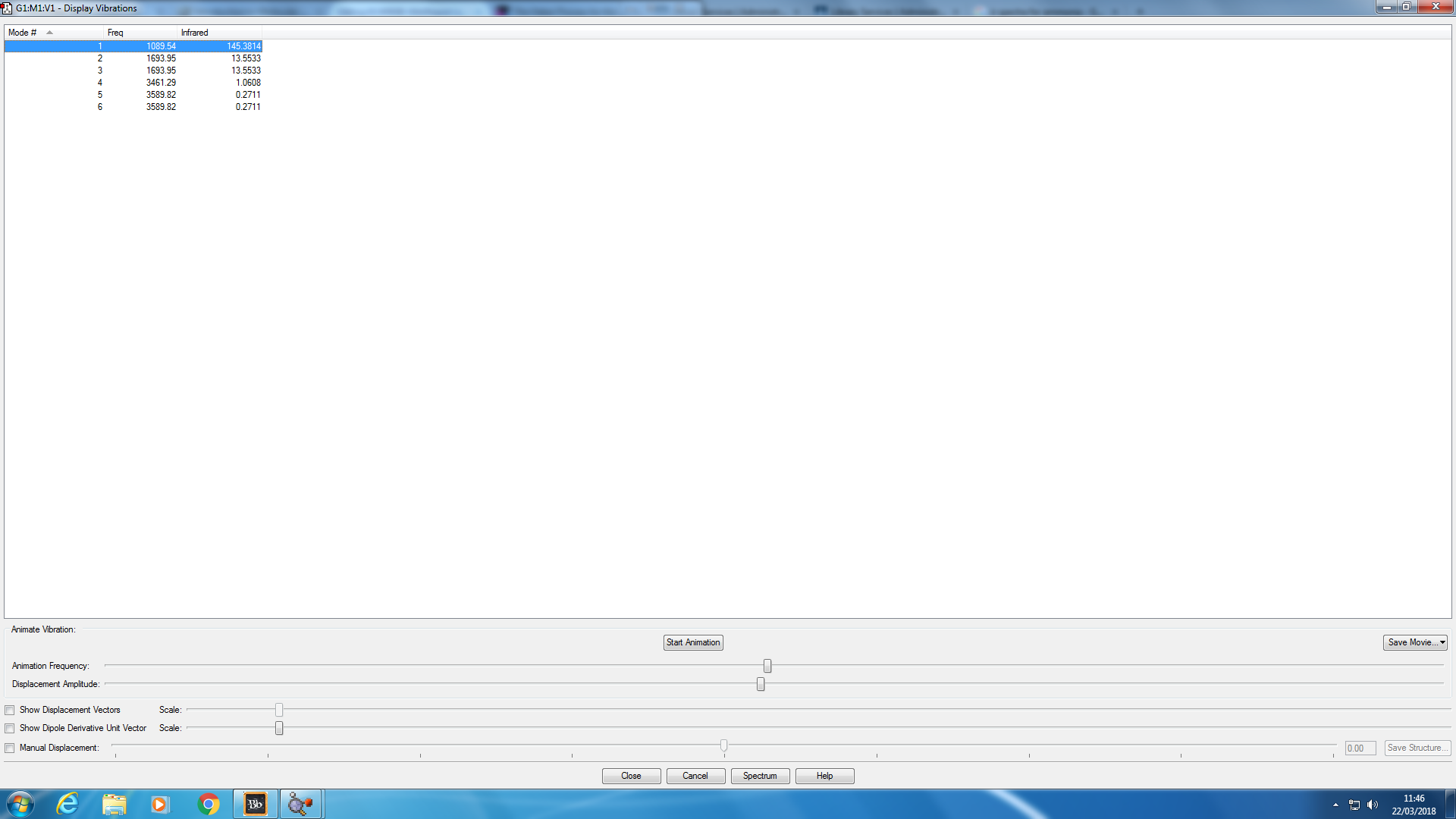
Animating Vibrations
I expected there to be 6 vibrational modes from the 3N-6 rule as N=4 and (3*4)-6=6. Modes 2&3 are degenerate and modes 5&6 are also degenerate. Modes 1,2&3 are all bending modes as they're lower in energy, whereas modes 4,5&6 are all stretching modes. Mode 4 is highly symmetric. The mode known as the umbrella mode is mode 1. In an experimental spectrum of gaseous ammonia I would expect to see 4 bands, as two states have degenerate stretches/bends, and all of the vibrational modes result in a change in dipole moment so they're all going to be infrared active. However, the two highest wavenumber bands would be almost invisible on a scaled spectra s their relative intensities are so small compared to the vibrations of a lower frequency.
Charge Analysis
By using Gaussian to calculate the charge on the Nitrogen and Hydrogen atoms, it showed that the charge on the central nitrogen atom was -1.125 and the hydrogen's surrounding all had a charge of +0.375. I expected the nitrogen to have a negative charge and the hydrogen to have a positive charge as nitrogen is more electronegative than hydrogen and so will withdraw electron density from hydrogen, leaving it being more negative while hydrogen is left to be more positive.
N2 Molecule
Running an optimization
Calculation method- RB3LYP
Basis set- 6-31G(d,p)
Final energy (au)- -109.52412868
RMS gradient- 0.0000006
Point group- DinfinH
N-N Bond length- 1.10550 angstroms
N-N bond angle- 180 degrees
Item Value Threshold Converged? Maximum Force 0.000001 0.000450 YES RMS Force 0.000001 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000000 0.001200 YES
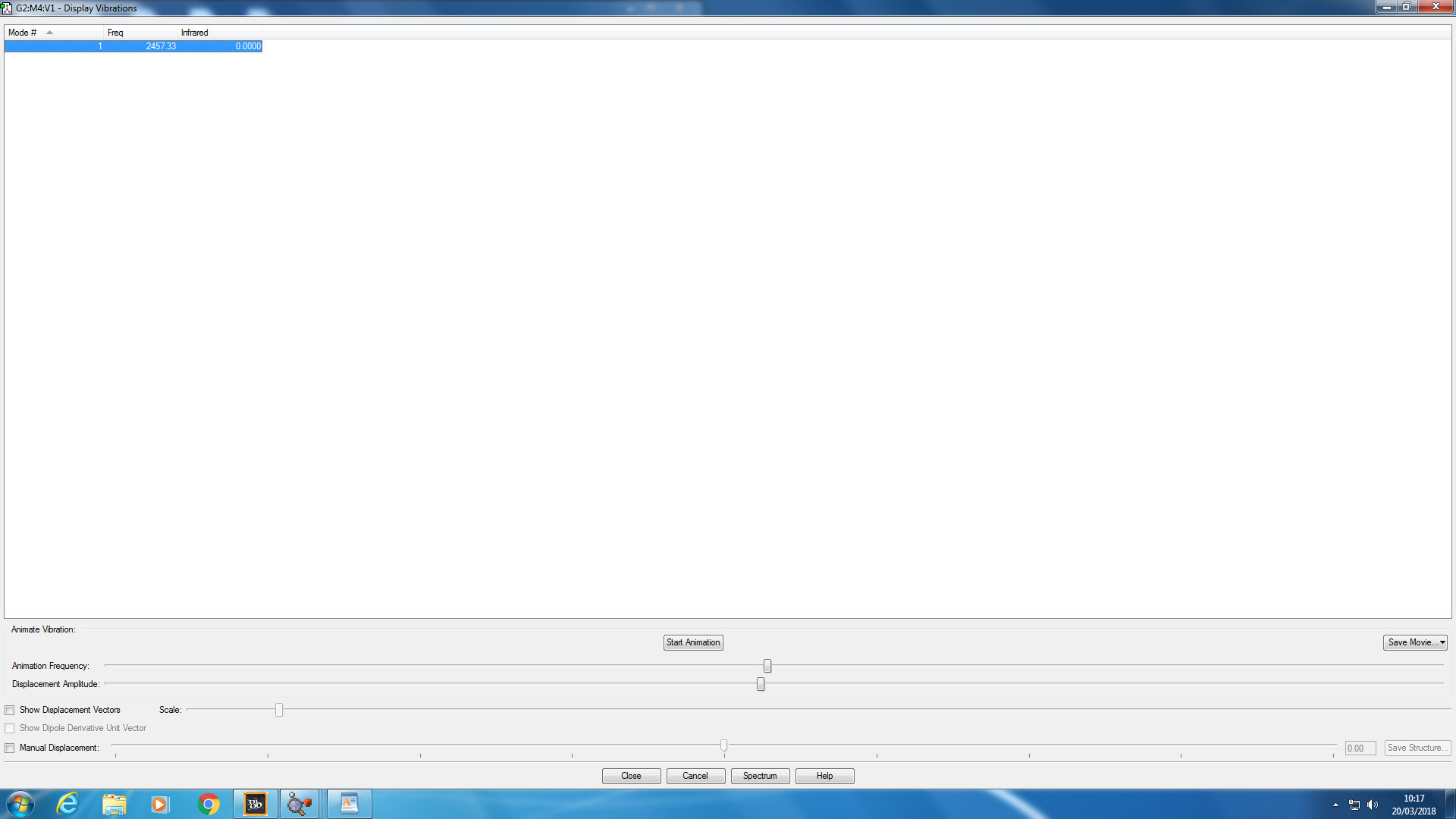
Animating Vibrations
The list of only one positive vibration frequency shown in the screenshot below confirms that there are no negative frequencies for this N2 molecule as expected.
H2 Molecule
Running an optimization
Basis set- 6-31G(d,p)
Final energy (au)- -1.17853936
RMS gradient- 0.00000017
Point group- DinfinH
H-H Bond length- 0.74279 angstroms
H-H bond angle- 180 degrees
Item Value Threshold Converged? Maximum Force 0.000000 0.000450 YES RMS Force 0.000000 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000001 0.001200 YES
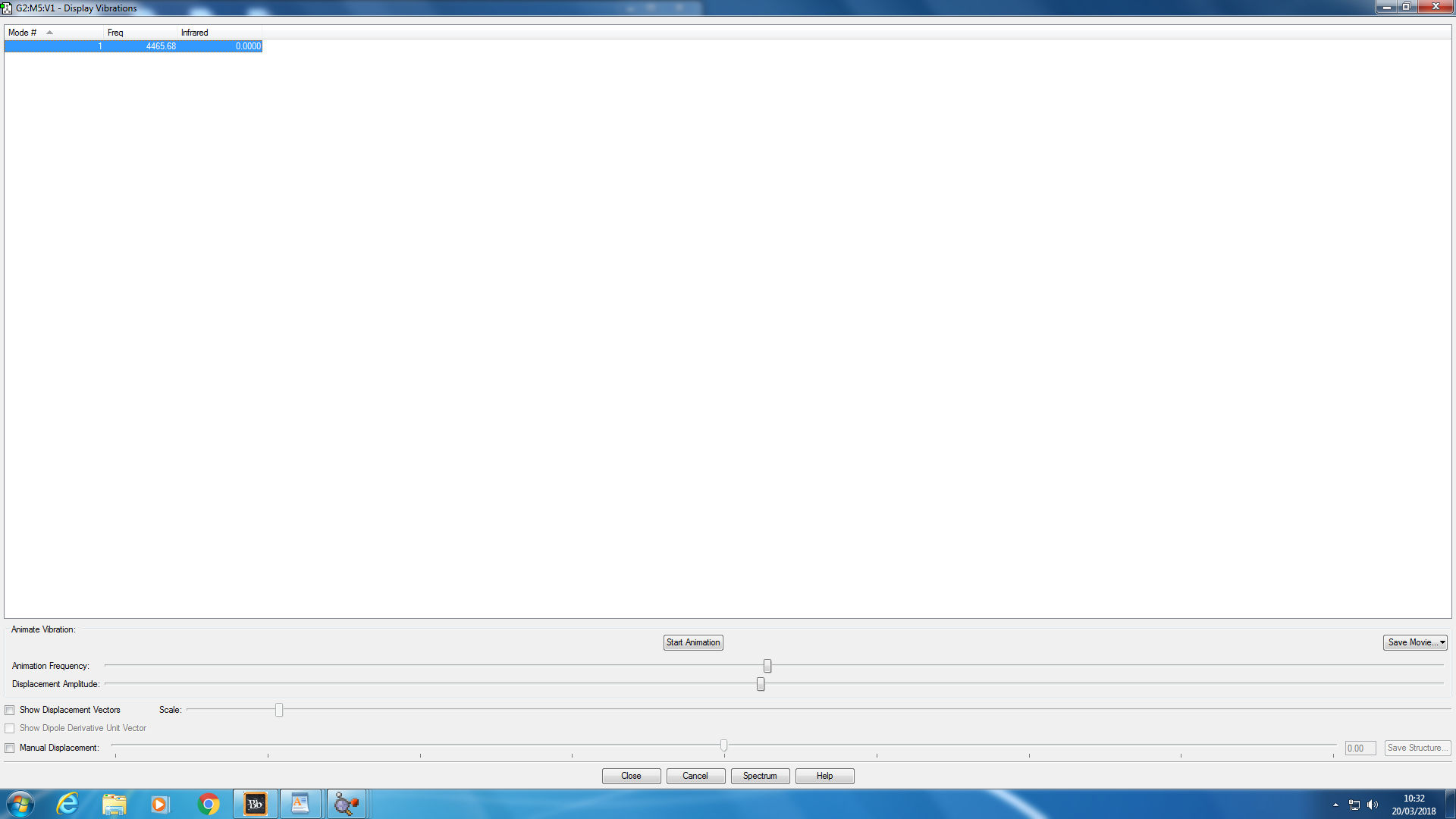
Animating Vibrations
The screenshot of the vibration frequency below shows one vibrating mode for the H2 molecule and it is positive as expected.
Haber reaction energy calculation
The Equation: N2 + 3H2 -> 2NH3
E(NH3)= -56.55776873au
2*E(NH3)= -113.1155375au
E(N2)= -109.52412868au
E(H2)= -1.17853936au
3*E(H2)= -3.53561808au
ΔE=2*E(NH3)-[E(N2)+3*E(H2)]= -0.0557904au = -146.4785879kJ/Mol
The ammonia gaseous product is more stable than the gaseous products as the sign for the energy change of the reaction is negative and so exothermic. In turn this means the reaction is favorable according to thermodynamics and in turn the product must be more stable than the reactants. The literature value for the energy of the reactions is -92kJ/Mol(1). This suggests that my reaction is actually more exothermic and thus more favourable than the real reaction. This can be explained as i used completely optimised structures to determine the energies. However, in real life the molecules would not be in their lowest energy states (most optimised states) when reaction, and high temperatures would distort this even more, so the reaction would be less favourable as collisions would not be successful as often.
Project Molecule- Phosphorane PH5
Running an optimization
Basis set- 6-31G(d,p)
Final energy (au)- -344.25491049
RMS gradient- 0.00000471
Point group- D3H
H-P Bond length- 1.48687/1.43316 angstroms (axial/equatorial)
H-P-H bond angle - 90/120 degrees (axial/equatorial)
Item Value Threshold Converged? Maximum Force 0.000009 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000055 0.001800 YES RMS Displacement 0.000022 0.001200 YES
Charge Analysis
The central phosphorus atom is more electropositive than the surrounding hydrogen atoms. Its formal charge in this case is +0.412. There are different hydrogen atoms in different environments around the phosphorus and so they don't all take the same formal charge value. Three of the hydrogens take a formal charge value of -0.015 and the remaining two take a value of -0.183. The hydrogens with the more negative charge are in the axial positions, as they're less affected by the partial positive charge created by the more electrospositve phosphorus.
Vibration frequency analysis
The figure below shows the 12 frequencies of vibration PH5 exhibits. These frequencies are analysed below the image. [[File:ph5vib.png] This is a non linear molecule so the number of vibrational modes expected is 3N-6 which is equal to 10 in this case as N=6. This is reflected by the above figure which shows the twelve vibrational modes. There are four sets of degenerate vibrations in the molecule. Modes 1&2, 4&5, 6&7 and 11&12 are degenerate pairs, meaning they have the same frequency of vibration. Vibrational modes 1-7 inclusive are bending modes, and 8-12 are stretches. Mode 10 is a highly symmetric stretch. The degenerate pairs of virbtaions will be indistinguishable on a spectrum and there must be a change in dipole moment for it too appear. Modes 6,7,8 and 10 do not result in a change in permanent dipole. This means that i would expect to see 5 spectral peaks for this molecule.
Molecular orbital analysis
The above figure shows the favourable interaction between the 3s atomic orbital of the central phosphorus atom with the 1s atomic orbitals on the surrounding hydrogen atoms. This is a bonding orbital.
The above figure shows the combination of the 3Px orbital on the central phosphorus atom with the 1s atomic orbitals on the 3 equatorial hydrogens around the central atom. The means that the two axial hydrogens are not involved in this orbital overlap. Due to the shorted bond length from the phosphorus and the equatorial hydrogens, a better overlap in orbitals is observed and so this molecular orbital is lower in energy (-0.42682au) than the 3Py interaction with the 1s atomic orbital on the axial hydrogens as shown below. This is a bonding orbital.
The above figure shows the previously mentioned combination of the 3Py atomic orbital on the central phosphorus with the 1s atomic orbitals on the two axial hydrogens, with an energy of -0.40948au, which is higher than the 3Px overlap, as previously discussed. It is also a bonding orbital.
The above figure shows the highest occupied molecular orbital for the PH5 compound. It is the combination of the sp3d hybridised orbital on the central phosphorus atom with the 1s atomic orbitals on the surrounding 5 axial and equatorial hydrogen atoms. It has an energy of -0.21463au meaning it is the last molecular orbital that is negative and thus is the last one where combination of orbitals is favourable. This is a bonding orbital.
Finally, the above figure shows the lowest unoccupied molecular orbital. Due to the fact that the molecular orbital is unoccupied, it can interact with a nucleophile as it can accept an electron pair into the LUMO. This is a non-bonding orbital.
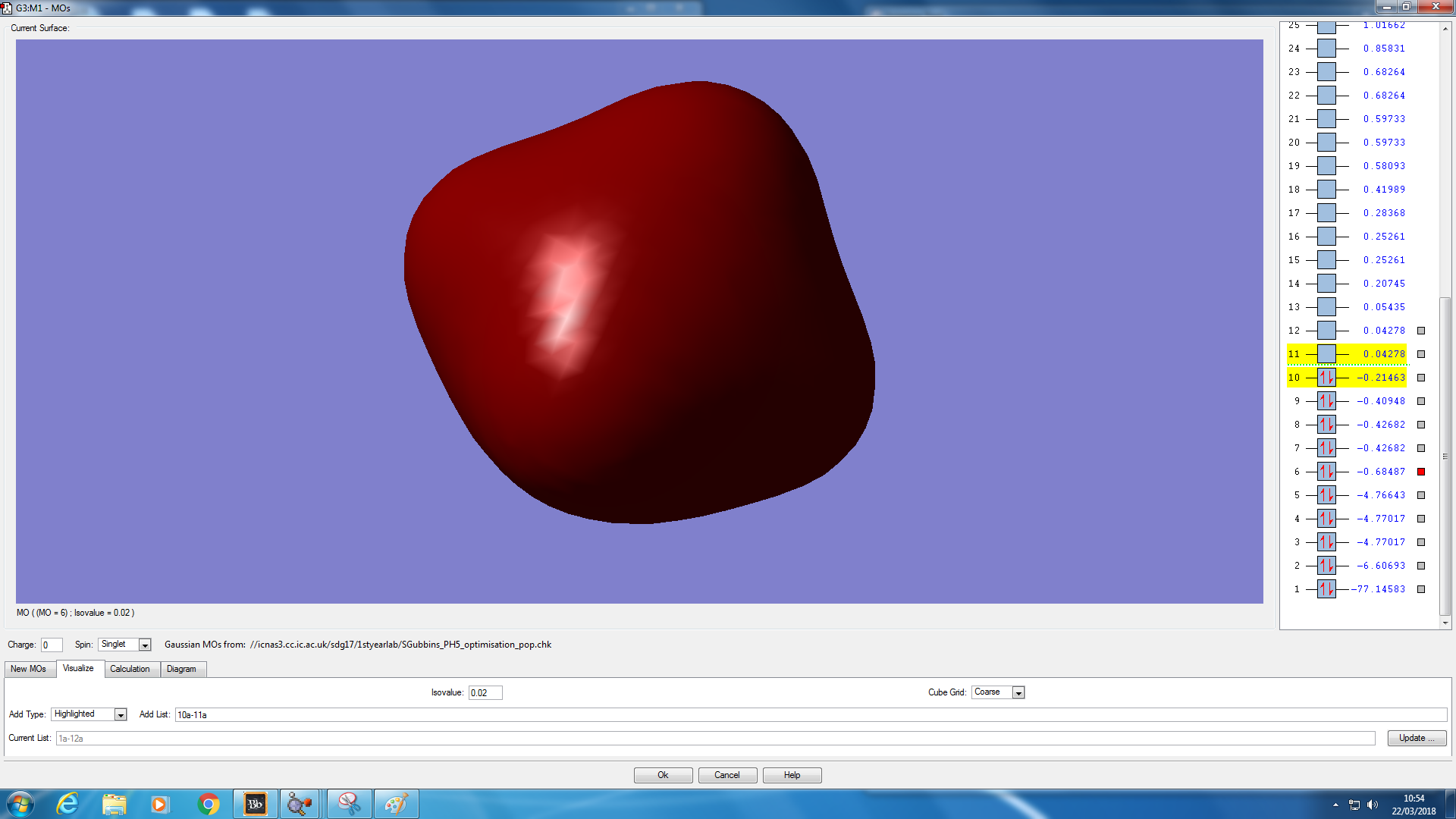
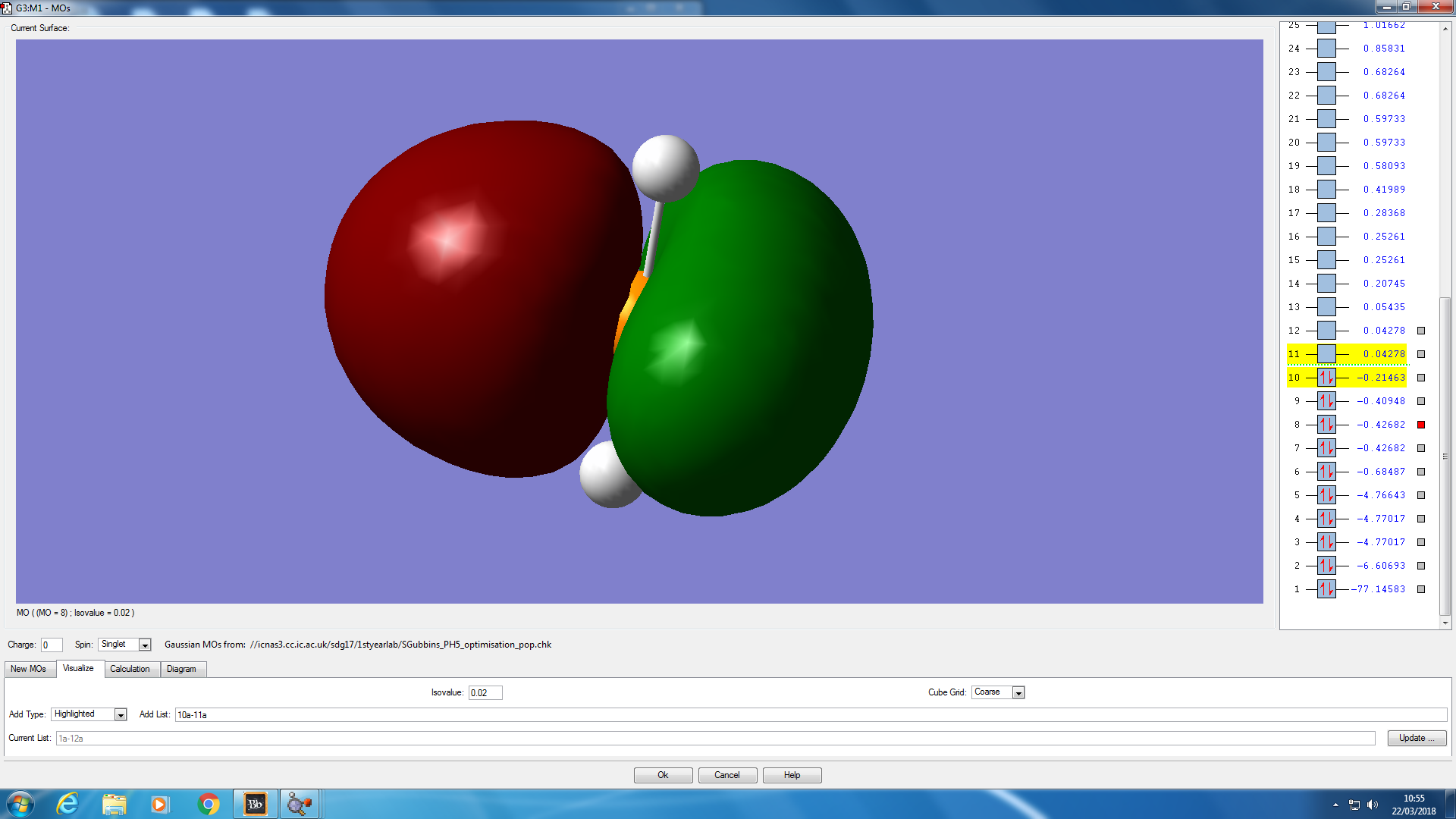
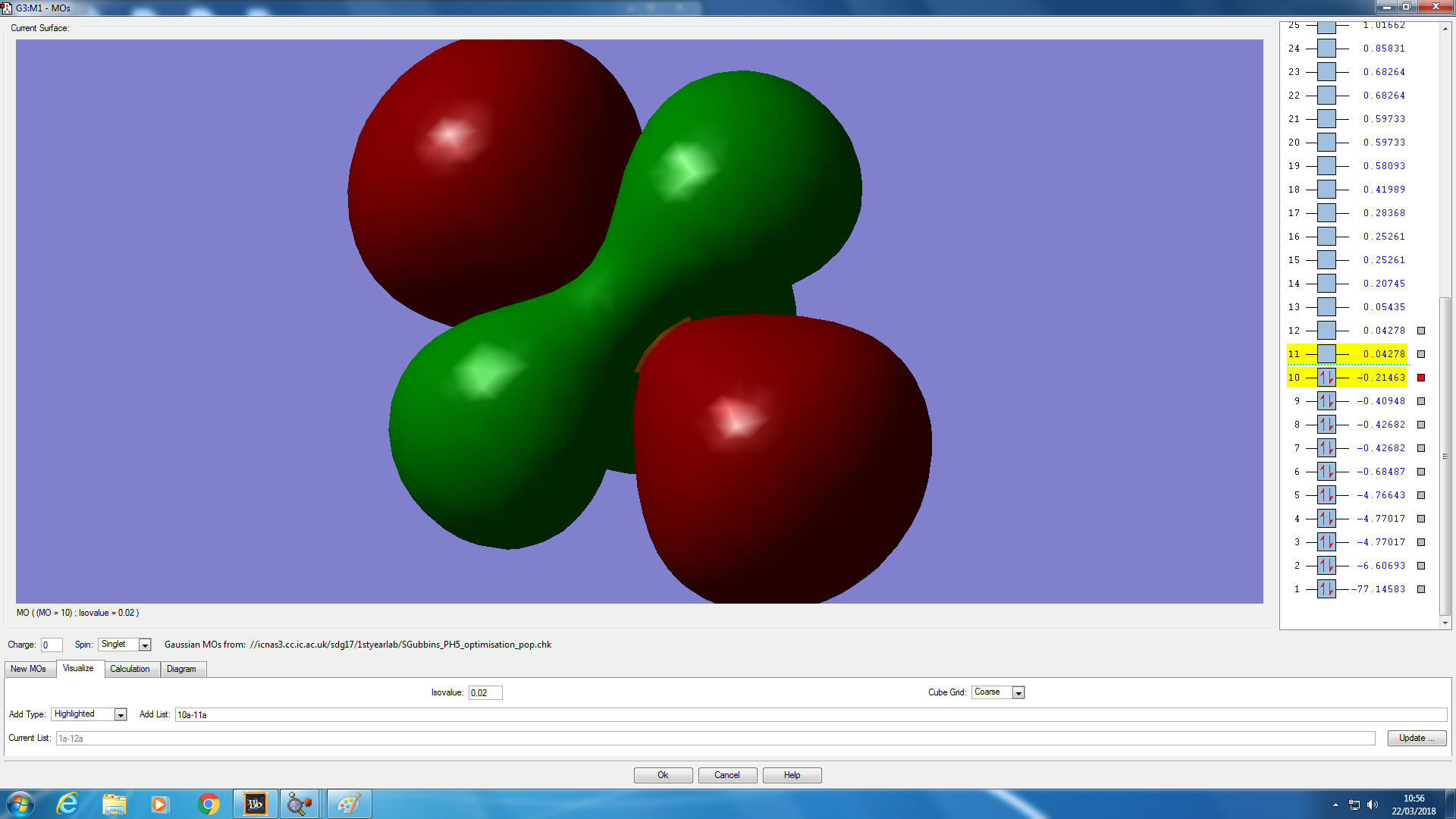
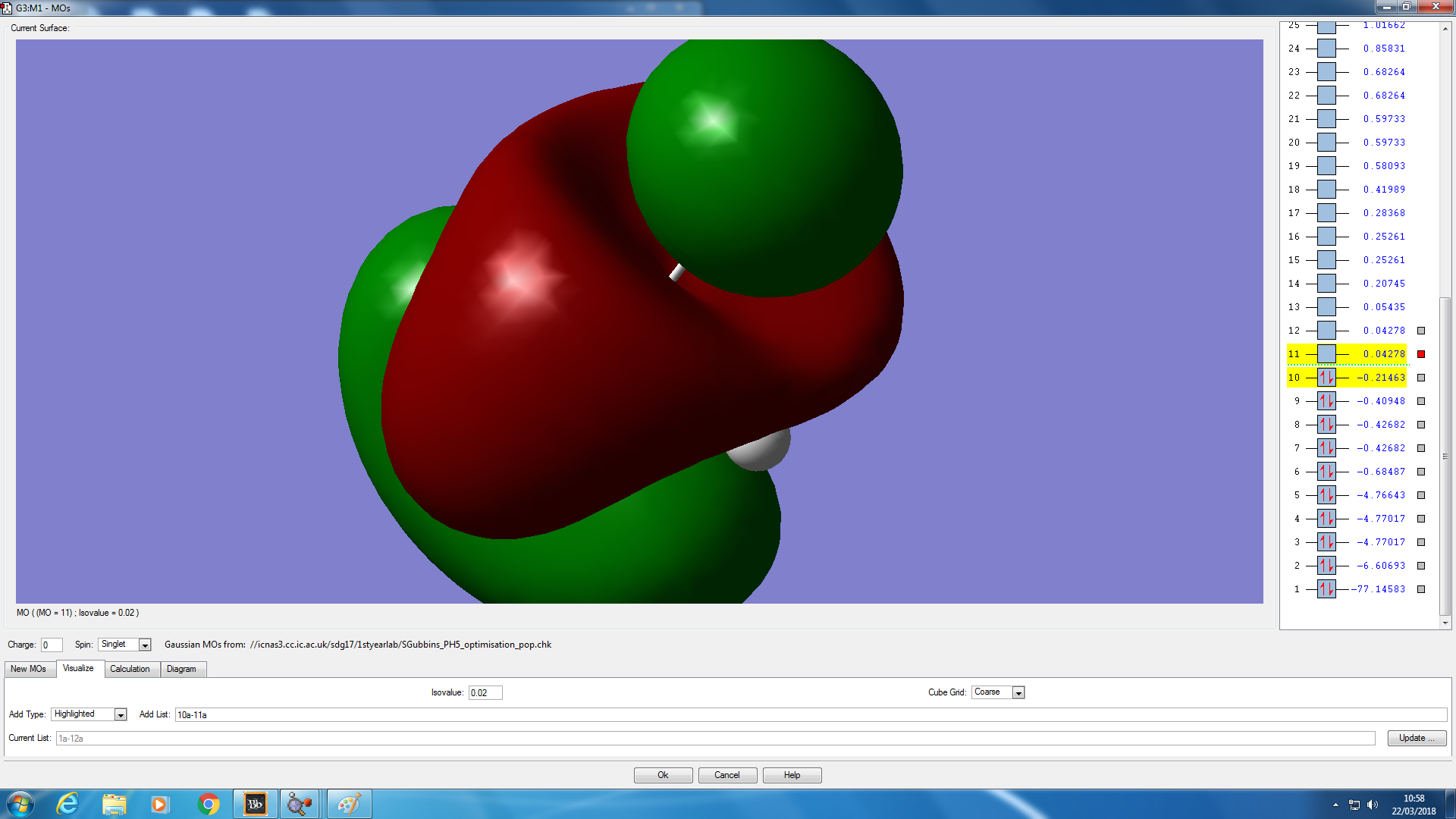
JMol of PH5 optimised
PH5 Molecule |
The optimisation file is liked to here
References
Haber process
(1)- Jim Clark for ChemGuide 2002 (modified 2013) https://www.chemguide.co.uk/physical/equilibria/haber.html