01333464 wikireport
NH3
Summary of optimisation
Calculation method- RB3LYP
Basis set-6-31G(d,p)
Final energy E(RB3LYP)- -56.55776873 a.u
RMS gradient- 0.00000485
Point group- C3v
NH Bond length- 1.01798 Å
H-N-H Bond angle- 105.741°
Item Value Threshold Converged? Maximum Force 0.000004 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000072 0.001800 YES RMS Displacement 0.000035 0.001200 YES
Viewing and optimisation
Ammonia molecule |
The optimisation file is linked to here
Vibrational analysis
Table of vibrational modes
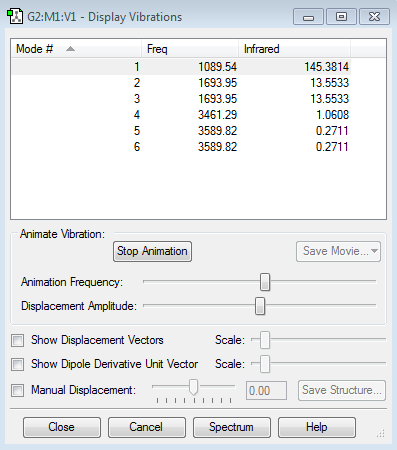
how many modes do you expect from the 3N-6 rule? I would expect 6 vibrational modes as there are 4 atoms and so 3(4)-6=6 which modes are degenerate (ie have the same energy)? Modes 2 and 3 are degenerate and modes 5 and 6 are degenerate as they have the same vibrational energies. which modes are "bending" vibrations and which are "bond stretch" vibrations? Modes 1-3 are bending vibrations and modes 4-6 are stretching vibrations. which mode is highly symmetric? Mode 4 is highly symmetric. one mode is known as the "umbrella" mode, which one is this? Mode 1 is known as the umbrella mode. how many bands would you expect to see in an experimental spectrum of gaseous ammonia? You would expect to see 4 bands as you have two sets of degenerate stretches. However the bands of modes 4 and the degenerate states 5 and 6 have very small intensities so on a real spectrum you would only really expect to see 2 bands corresponding to modes 1 and the degenerate modes 2 and 3.
Charge analysis
The charge on the N-atom is -1.125 and that of the H-atom is +0.375. This is expected as the N-atom has a negative charge and the H-atom has a positive charge due to Nitrogen being more electronegative and hence pulls electron density closer to itself.
NH2
Summary of optimisation
Calculation method- RB3LYP
Basis set- 6-31G(d,p)
Final energy E(RB3LYP)- -109.52412868 a.u
RMS gradient- 0.0000006 a.u
Point group- D∞h
N-N Bond length- 1.10550 Å
N-N Bond angle- 180°
Item Value Threshold Converged? Maximum Force 0.000001 0.000450 YES RMS Force 0.000001 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000000 0.001200 YES
The one positive frequency shows that there are no negative frequencies as expected.
H2
Summary of optimisation
Calculation method- RB3LYP
Basis set- 6-31G(d,p)
Final energy E(RB3LYP)- -1.17853936 a.u
RMS gradient- 0.00000017 a.u
Point group- D∞h
N-N Bond length- 0.74279 Å
N-N Bond angle- 180°
Item Value Threshold Converged? Maximum Force 0.000000 0.000450 YES RMS Force 0.000000 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000001 0.001200 YES
The one positive frequency shows that there are no negative frequencies as expected.
Energy calculation for N2 + 3H2 -> 2NH3
E(NH3)= -56.55776873 a.u 2*E(NH3)= -113.1155375 a.u E(N2)= -109.52412868 a.u E(H2)= -1.17853936 a.u 3*E(H2)= -3.53561808 a.u ΔE=2*E(NH3)-[E(N2)+3*E(H2)]= -0.05579074 a.u = -146.4785879 kJ/mol
The ammonia product is more stable as the negative sign indicates this is an exothermic reaction and the product is lower in energy than the reactant. This is because the ammonia compound is lower in energy than the sum of its individual molecules hydrogen and nitrogen.
The literature value of the reaction is -92.4 kJ/mol (1). The difference in this is value and our value is due to the fact that the program optimized the molecules in conditions that do not reflect a real life in lab situation that the molecules would exist in. This means that the energy values for the molecules would be higher in energy and thus give an overall higher value for the ΔE.
Phosphorane PH5
Summary of optimisation
Calculation method- RB3LYP
Basis set-6-31G(d,p)
Final energy E(RB3LYP)- -344.25491049 a.u
RMS gradient- 0.00000471
Point group- D3h
PH Bond length (axial) - 1.48687 Å
PH Bond length (equatorial) - 1.43316 Å
H-P-H Bond angle (axial) - 90°
H-P-H Bond angle (equatorial) - 120°
Phosphorane molecule |
The optimisation file is linked to here
Charge analysis
The axial hydrogen atoms have a charge of -0.183 and the equatorial hydrogen atoms have a charge of -0.015 while the central phosphorous atom has a charge of +0.412. The signs of these charges are expected because the central phosphorous atom is more electropositive than the surrounding hydrogen atoms. The axial hydrogens are further away than the equatorial hydrogens so are less effected by the positive charge on the phosphorous.
Vibrational analysis
how many modes do you expect from the 3N-6 rule? I would expect 12 vibrational modes as there are 6 atoms and so 3(6)-6=6
which modes are degenerate (ie have the same energy)? Modes 1 and 2, 4 and 5, 6 and 7, 11 and 12 are degenerate as they have the same vibrational energies.
which modes are "bending" vibrations and which are "bond stretch" vibrations? Modes 1-7 are bending vibrations and modes 8-12 are stretching vibrations.
which mode is highly symmetric? Mode 10 is highly symmetric.
how many bands would you expect to see in an experimental spectrum? You would expect to see 5 bands as modes 2,5,7 and 12 are degenerate and modes 6,7,8 and 10 and will not be seen due to selection rules (no change in permanent dipole moment).
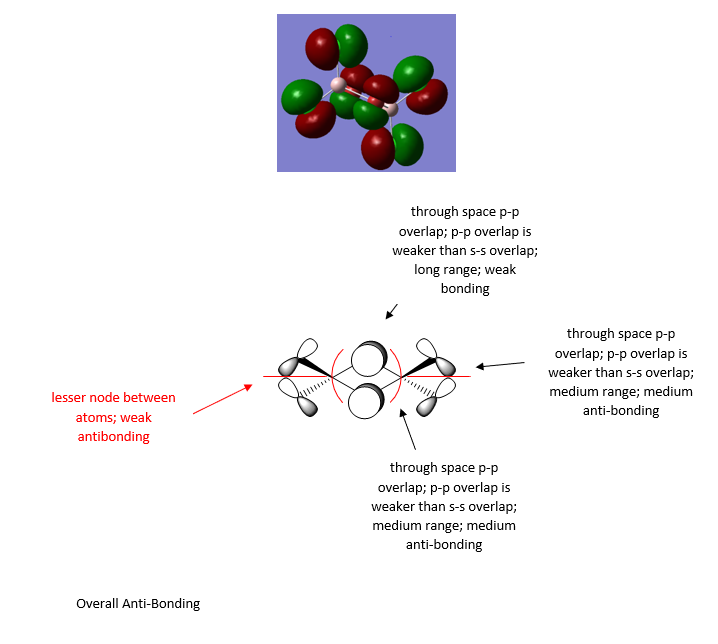
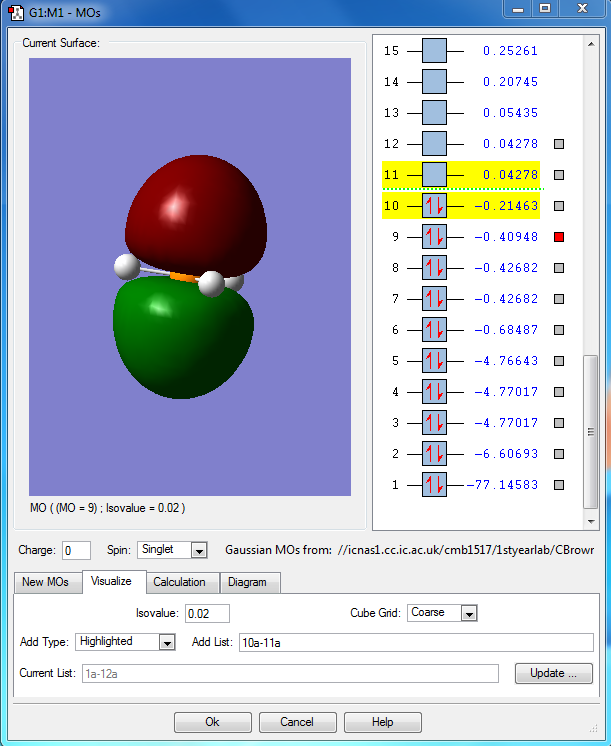
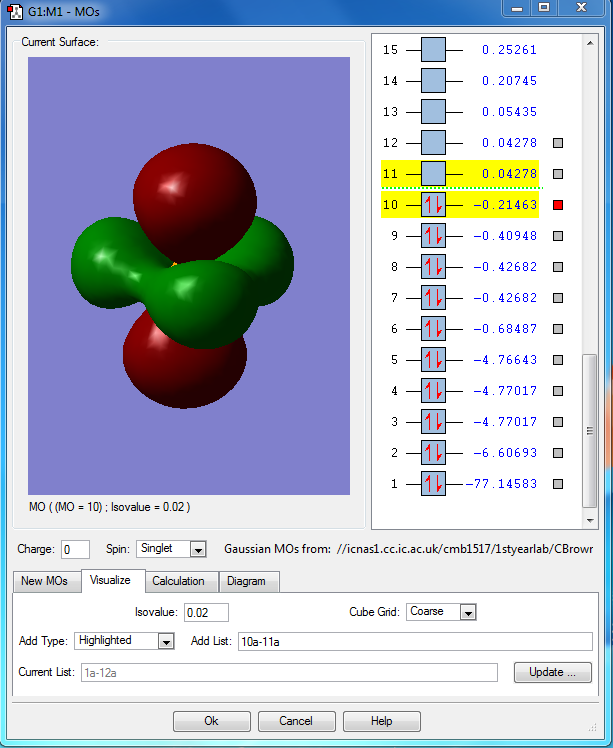
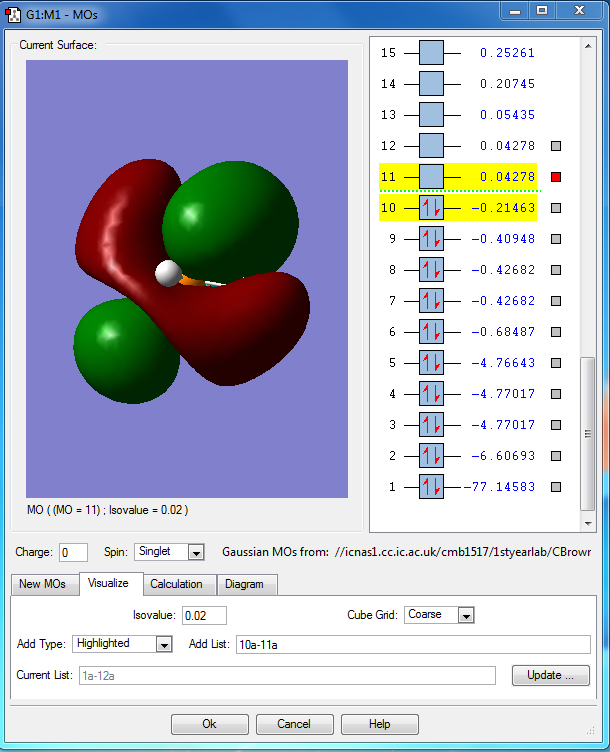
PH5 molecular orbital analysis
The following molecular orbitals are some of the orbital solutions to the Schrödinger equation
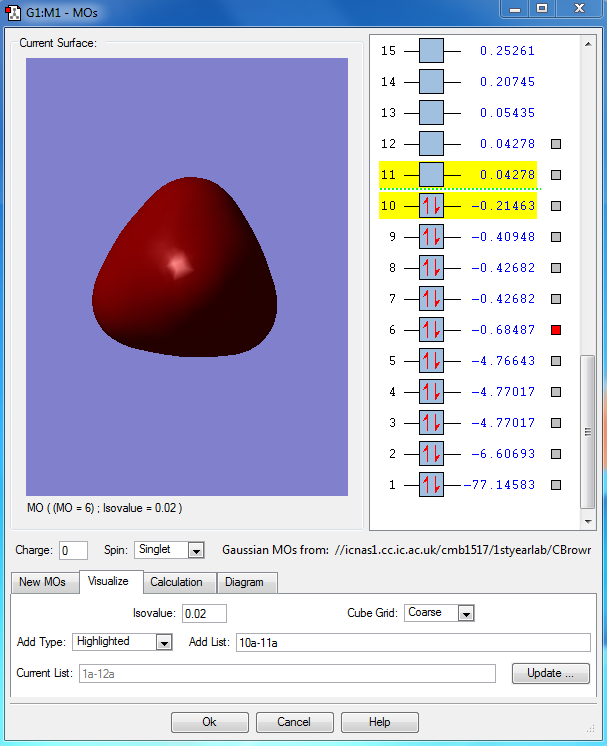
This is the combination of the 3s atomic orbital of the central phosphorous atom and the 1s orbitals of the 5 hydrogen atoms. This is an occupied bonding molecular orbital which is deep in energy.
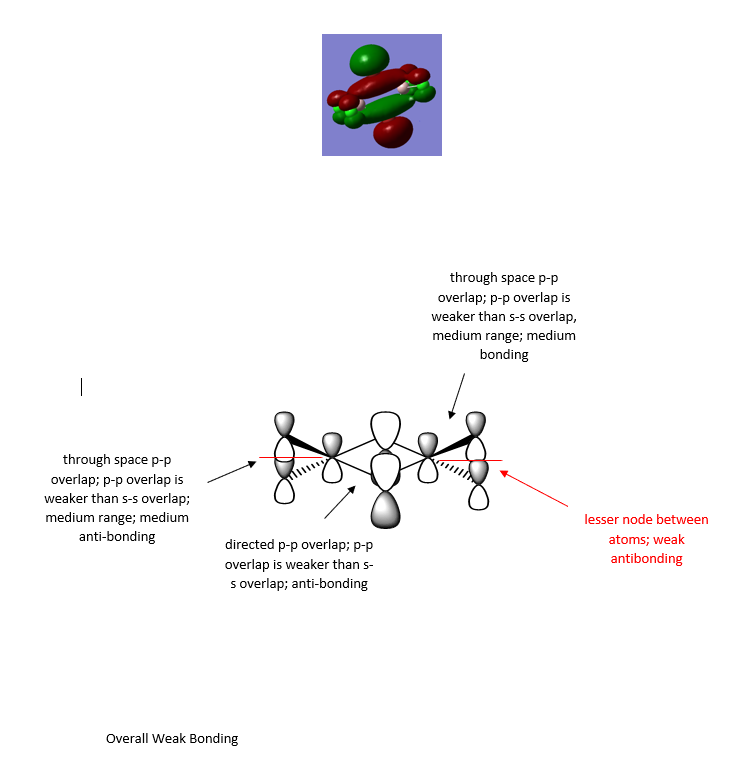
This is the combination of the 3px atomic orbital on the central phosphorous atom and the 1s atomic orbitals of the 3 equatorial hydrogen atoms. The 1s orbitals of the axial hydrogen atoms are not involved. This molecular orbital is lower in energy than the molecular orbital interaction of the combined 3py and the 1s orbitals of the axial hydrogen's because they are closer to the phosphorous and get a better overlap. This is an occupied bonding molecular orbital which is deep in energy.
This molecular orbital is the combined 3py of the phosphorous and the two 1s orbitals of the axial hydrogen's. This is an occupied bonding molecular orbital which is deep in energy.
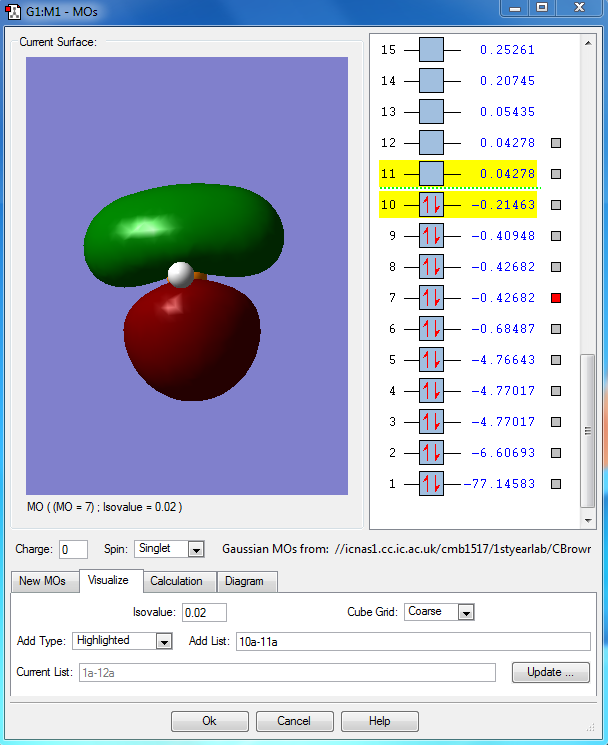
This is highest occupied molecular orbital (HOMO) of the phosphorane molecule. It is the combination of the hybridised sp3d orbital of the phosphorous atom with the 5 1s atomic orbitals on the hydrogen atoms. This is a bonding molecular orbital which is deep in energy.
This is the lowest unoccupied molecular orbital (LUMO) of the phosphorane molecule. This is the molecular orbital that would accept a pair of electrons from a nucleophile if it were to be attacked. This is an unoccupied non bonding molecular orbital which is higher in energy.
References
(1) -https://www.chemguide.co.uk/physical/equilibria/haber.html