01234587
Ammonia
Calculation Method = RB3LYP
Basis set = 6-31G(d,p)
E(RB3LYP) = -56.55776873 a.u.
RMS Gradient = 0.00000485 a.u.
Point Group = C3V
Item Value Threshold Converged? Maximum Force 0.000004 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000072 0.001800 YES RMS Displacement 0.000035 0.001200 YES
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.018 -DE/DX = 0.0 !
! R2 R(1,3) 1.018 -DE/DX = 0.0 !
! R3 R(1,4) 1.018 -DE/DX = 0.0 !
! A1 A(2,1,3) 105.7412 -DE/DX = 0.0 !
! A2 A(2,1,4) 105.7412 -DE/DX = 0.0 !
! A3 A(3,1,4) 105.7412 -DE/DX = 0.0 !
! D1 D(2,1,4,3) -111.8571 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
Ammonia |
click here for the optimisation file
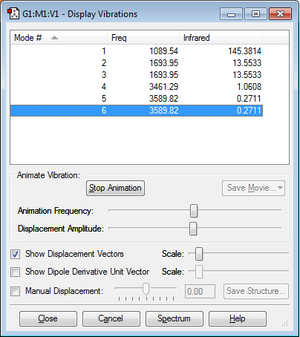
According to the 3N-6 rule, 6 vibrational modes can be expected (3*4-6). The degenerate modes are the second and the third (1693.95), and the fifth and the sixth (3589.82). Modes 4, 5 and 6 are stretching modes, modes 1, 2 and 3 are bending modes. Mode 4 is highly symmetric. Mode 1 is known as the "umbrella mode". We can expect to see 4 bands in the spectrum.
Charge of N = -1.125
Charge of H = 0.375
We can expect a negative charge on the N atom because it is more electronegative than the H atoms, therefore it is drawing electrons towards itself, whereas on the H atoms there will be a positive charge, since their electrons are further from the nucleus.
The N-H bond length is 1.01798Å, the H-N-H angle is 105.74°.
Nitrogen
Calculation Method = RB3LYP
Basis set = 6-31G(d,p)
E(RB3LYP) = -109.52359111 a.u.
RMS Gradient = 0.02473091 a.u.
Point group = D*H
Item Value Threshold Converged? Maximum Force 0.000001 0.000450 YES RMS Force 0.000001 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000000 0.001200 YES
Nitrogen |
click here for the optimisation file
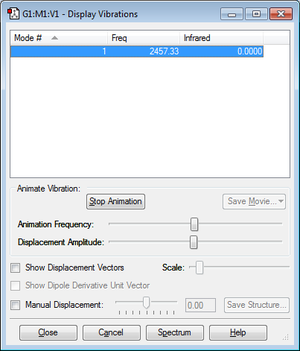
As it can be seen, there are no negative frequencies. The distance between the atoms is 1.10550Å.
Hydrogen
Calculation Method = RB3LYP
Basis set = 6-31G(d,p)
E(RB3LYP) = -1.17853936 a.u.
RMS Gradient = 0.00000017 a.u.
Point Group = D*H
Item Value Threshold Converged? Maximum Force 0.000000 0.000450 YES RMS Force 0.000000 0.000300 YES Maximum Displacement 0.000000 0.001800 YES RMS Displacement 0.000001 0.001200 YES
Hydrogen |
click here for the optimisation file
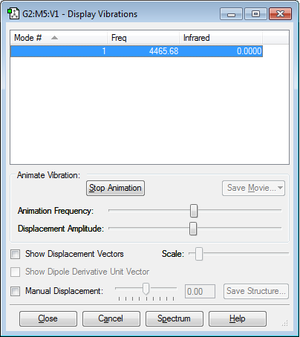
The distance between the atoms is 0.74279Å.
Haber-Bosch Process
E(NH_3) = -56.55776837 a.u.
2E(NH_3) = -113.1155375 a.u.
E(N_2) = -109.52359111 a.u.
E(H_2) = -1.17853936 a.u.
3E(H_2) = -3.53561808 a.u.
ΔE=2E(NH_3)-[E(N_2)+3E(H_2)] = -0.05632831 a.u. = -147.8899779 kJ/mol
The experimental value of the standard enthalpy of formation of ammonia is actually -45.9 kJ/mol. This discrepancy is due to the fact that the calculations are purely theoretical. The experimental value is lower than the calculated one and this means that the process of fixation of the dinitrogen molecule will still be exothermic. However, the process is not spontaneous because the breaking of the triple bond in nitrogen is a high energy barrier that has to be overcome. The value of the bond dissociation energy in N2 is 941 kJ/mol. Thus, this energy has to be supplied to the system to initiate the reaction that will lead to the formation of NH3.[1] Ammonia has a wide range of uses and it is primarily important as a fertiliser. The Haber-Bosch process catalyses the reaction combining high temperatures (450°C), high pressures (100 up to 300 atm) and an iron catalyst.[2] The amount of energy needed to carry out this process, however, consumes about 1.1% of all the energy resources worldwide each year.[1] It is vitally important, therefore, to find other methods to catalyse the reaction and, particularly, heterogeneous catalysts which could lead to a facile fixation of the N2 molecule.
Carbon Monoxide
Charge and bond length
O = -0.506 C = 0.506
C-O bond length = 1.13729Å
The signs are predictable, O is more electronegative than C, therefore it will attract the electron density on itself.
Optimisation
Calculation Method = RB3LYP
Basis Set = 6-31G(d,p)
E(RB3LYP) = -113.30945314 a.u.
RMS Gradient Norm = 0.00001828 a.u.
Point Group = C*V
Item Value Threshold Converged? Maximum Force 0.000032 0.000450 YES RMS Force 0.000032 0.000300 YES Maximum Displacement 0.000012 0.001800 YES RMS Displacement 0.000018 0.001200 YES
Optimisation file
click here for the optimisation file
Vibrations
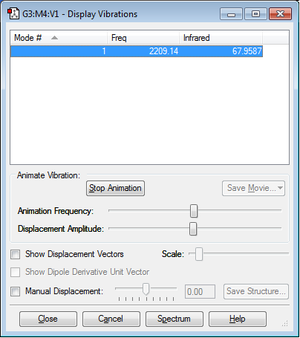
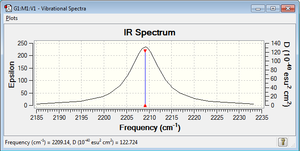
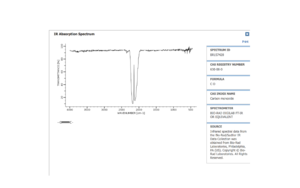
As it can be seen, there is a single vibration. Being a linear diatomic molecule, 3N-5=1. It is a stretch and the frequency is quite low (a triple bond is very strong). Compared to an experimental spectrum[3], the one obtained is quite similar. There is no splitting in the peak in the theoretical one.
Molecular Orbitals
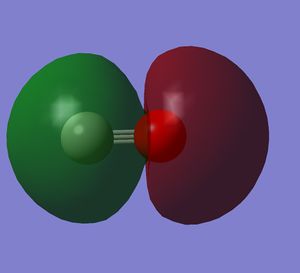

It is an antibonding orbital formed by the two 2s orbitals.
Note how the 2π orbitals formed have the same geometry and the same energy. They are degenerate and indistinguishable.
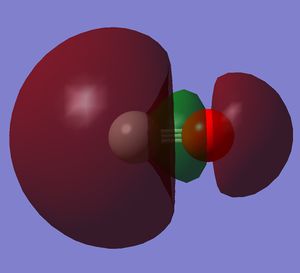
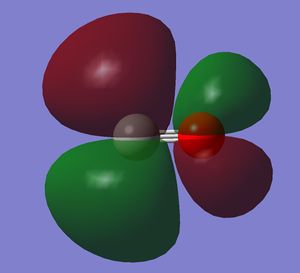
It is the HOMO. It is a bonding orbital generated by two 2p orbitals. There is mixing with the 2s orbitals.
It is an unoccupied orbital, therefore it is purely theoretical. It is the LUMO in the molecule

Looking at the oxygen atom, it can be seen that there is electron density around it, inside the electron density in the other phase. Being an unoccupied orbital, it is purely theoretical.
The molecular orbitals formed by 1s orbitals are not shown because they are very deep in energy and do not give a significant contribution to the bond.
Hydrazine
What is hydrazine?
Hydrazine is a derivative of ammonia with molecular formula N2H4. It is liquid in approximately the same range of temperature of water (2-114°C) due to the presence of hydrogen bonding. It is normally manufactured via the Raschig process, which involves the reaction between ammonia and sodium hypochlorite in aqueous solution.[2] The standard enthalpy of formation of hydrazine is 95.35 kJ/mol[1]. Therefore, the breaking of the molecule will be a strongly exothermic process. Hydrazine and its derivatives are used as rocket fuel because of this property. The main problem with the production of hydrazine is that, since it is a derivative of ammonia, it relies heavily on the Haber-Bosch process which, as said, is energetically demanding. This adds to the cost of production of hydrazine itself, making it an extremely expensive process. A possible solution could derive from the study of catalysts which could directly convert N2 into hydrazine. The latest developments use an Fe catalyst to achieve the hydrogenation of nitrogen, skipping the production of ammonia.[4] The study of energy, charges and molecular orbitals in hydrazine is very important in order to understand its reactivity.
Analysis
Optimisation
Item Value Threshold Converged? Maximum Force 0.000170 0.000450 YES RMS Force 0.000047 0.000300 YES Maximum Displacement 0.000901 0.001800 YES RMS Displacement 0.000451 0.001200 YES
Item table for Hydrazine (1)
Item Value Threshold Converged? Maximum Force 0.000204 0.000450 YES RMS Force 0.000124 0.000300 YES Maximum Displacement 0.001416 0.001800 YES RMS Displacement 0.000911 0.001200 YES
Item table for hydrazine(2)
| Hyd 1 | Hyd 2 | |
|---|---|---|
| Calculation Method | RB3LYP | RB3LYP |
| Basis Set | 6-31G(d,p) | 6-31G(d,p) |
| E(RB3LYP) (a.u.) | -111.86865527 | -111.86580956 |
| RMS Gradient Norm (a.u.) | 0.00006290 | 0.00013565 |
| Point Group | C2 | C2 |
| Charges | N=-0.731 H1=0.354 H2=0.377 | N=-0.741 H=0.370 |
| N-N Bond Length | 1.43647pm | 1.48891pm |
Hydrazine(1), higher E conformation |
click here for the optimisation file
Hydrazine(2), lower E conformation |
click here for the optimisation file
Spectra
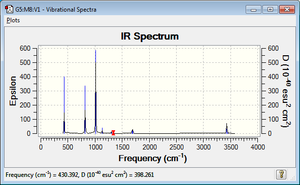
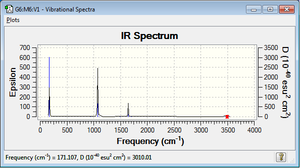

The theoretical IR spectrum is quite different from the experimental one,[3] probably because in the experimental ones there is the presence of a solvent
Molecular Orbitals

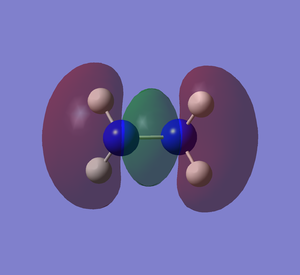
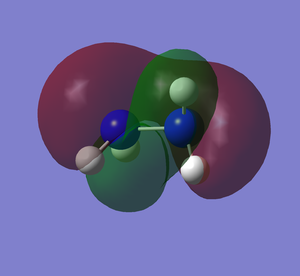
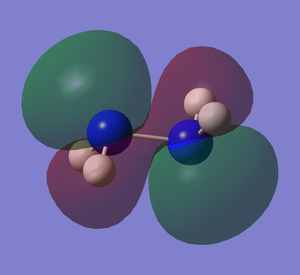
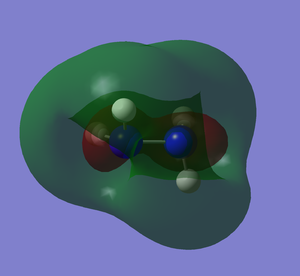
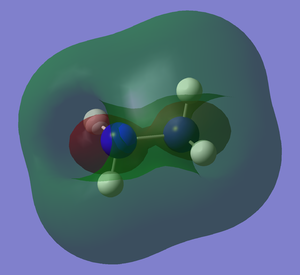
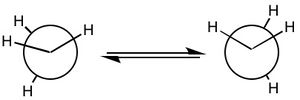
It can be seen how the two conformers of hydrazine have to be treated as two different molecules. In fact, they present a completely different shape of the HOMO and the other orbitals, deeper in energy. The LUMO, being the first unoccupied orbital, is a prediction based on calculations. Both of them have the same point group and 12 modes of vibration but with different energies. Curiously, the calculations show that the gauche conformation is the most energetic one, whereas it is empirically demonstrated that it is the most favourable one.[2] The fact that the gauche conformation is the most likely to be found could be explained saying that the molecule has to overcome a high energy barrier to reach the staggered conformation, whereas the energy barrier for the gauche conformation is lower. This results in a preferred gauche conformation.[5] Carrying out the calculations with another method (Hartree-Fock), the result confirmed that the gauche conformation is the most energetic one, but the program assigned another point group (C1) to this conformer. The structure of hydrazine and its conformational isomers, in theory, could be studied by NMR spectroscopy, since the chemical environments of the H atoms are different.
References
<references> [1] [2] [4] [5] [3]
- ↑ 1.0 1.1 1.2 1.3 Jia, H.-P.; Quadrelli, E. A. Chem. Soc. Rev. 2014, 43 (2), 547–564.
- ↑ 2.0 2.1 2.2 2.3 Overton, T., Rourke, Jonathan P., Weller, M., Armstrong, F. A. Inorganic Chemistry; Oxford University Press: Oxford, 2010.
- ↑ 3.0 3.1 3.2 3.3 3.4 https://scifinder.cas.org/scifinder/view/scifinder/scifinderExplore.jsf
- ↑ 4.0 4.1 Hill, P. J.; Doyle, L. R.; Crawford, A. D.; Myers, W. K.; Ashley, A. E. J. Am. Chem. Soc. 2016.
- ↑ 5.0 5.1 Jarvie, J. O.; Rauk, A. Can. J. Chem. 1974, 52
