01180512
NH3 molecule
Description and Calculation
NH3 molecule |
The NH3 molecule is one of the most impactful compounds, due to its use as an intermediate for synthesising fertilisers in agriculture, feeding billions around the world.[1] It is made from the haber proces by reacting Hydrogen gas with Nitrogen gas. Ammonia has many more uses as a solvent, a precursor to Nitrogen-based compounds and also as a cleaning agent.
| N-H bond distance | 1.01798 Å |
| H-N-H bond angle | 105.741° |
| Calculation Type | FREQ |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| Charge | 0 |
| Energy(RB3LYP) | -56.55776873 a.u., -148492.43 kJ/mol |
| RMS Gradient Norm | 0.00000485 a.u. |
| Imaginary Freq | 0 |
| Dipole Moment | 1.8466 Debye |
| Point Group | C3v |
Item Value Threshold Converged?
Maximum Force 0.000004 0.000450 YES
RMS Force 0.000004 0.000300 YES
Maximum Displacement 0.000072 0.001800 YES
RMS Displacement 0.000035 0.001200 YES
Predicted change in Energy=-5.986266D-10
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.018 -DE/DX = 0.0 !
! R2 R(1,3) 1.018 -DE/DX = 0.0 !
! R3 R(1,4) 1.018 -DE/DX = 0.0 !
! A1 A(2,1,3) 105.7412 -DE/DX = 0.0 !
! A2 A(2,1,4) 105.7412 -DE/DX = 0.0 !
! A3 A(3,1,4) 105.7412 -DE/DX = 0.0 !
! D1 D(2,1,4,3) -111.8571 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
Data from calculations are found here
Vibrational Modes
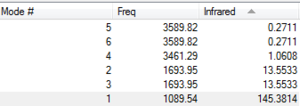
NH3 has 3N - 6 modes of vibration since it is a non-linear molecule. With 4 atoms, we expected 12 - 6 = 6 modes of vibration. This is reflected by precited vibrations of the GaussView Software.
Modes 2 and 3 are degenerate, Modes 5 and 6 are degenerate as reflected by their identical frequency.
Mode 4 is a highly symmetric stretch, Modes 5, 6 are asymmetric stretches. Modes 1, 2 and 3 are bending modes of vibration.
Mode 1 is umbrella mode.
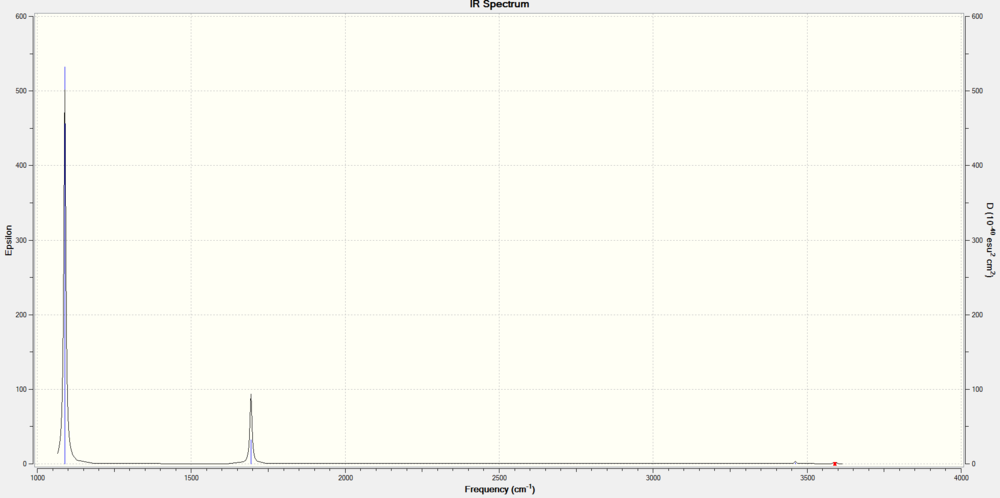
2 peaks are expected to be observed in the IR spectrum. To be IR active, a mode of vibration needs to result in a change in dipole moment. There are 2 degenerate pairs (2,3) and (5,6) of vibrational motion out of 6 modes of vibration. Degenerate modes of vibration result only in a singular peak. In addition, the symmetric(4) and asymmetric stretches(5,6) have minimal to no change in dipole moment, resulting in extremely low intensities of their predicted IR peaks. They are predicted to be IR inactive. The vibrational modes 1 and a degenerate pair (2,3) result in a significant net change in dipole moment and can be said to be IR active.
The frequencies of the IR spectrum are found to correspond to that of literature[2], but not completely, since rotational P, Q bands are observed in experimental IR spectrum, along with an additional peak. Intramolecular interactions like hydrogen bonding between NH3 are also not predicted by this software.
Charge Distribution
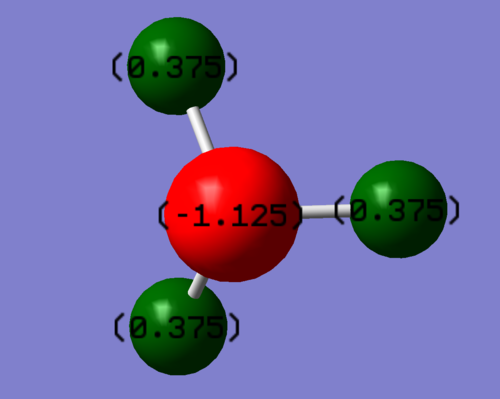
Charge distribution on N = - 1.125 a.u. Charge distribution on H = + 0.375 a.u.
This corresponds to expectations since N is more electronegative than H.
H2 molecule
H2 molecule |
| H-H bond distance | 0.74279 Å |
| Calculation Type | FREQ |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| Charge | 0 |
| Energy(RB3LYP) | -1.17853936 a.u., -3094.25 kJ/ mol |
| RMS Gradient Norm | 0.00000017 a.u. |
| Imaginary Freq | 0 |
| Dipole Moment | 0.0000 Debye |
| Point Group | D∞h |
Item Value Threshold Converged?
Maximum Force 0.000000 0.000450 YES
RMS Force 0.000000 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000001 0.001200 YES
Predicted change in Energy=-1.164080D-13
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 0.7428 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
Data from calculations are found here
Vibrational Modes

In accordance with the 3N - 5 rule for predicting the number of vibrational modes for linear molecules, H2 has only one symmetric stretch present. No net change of dipole moment occurs for the symmetric stretch, and H2 is not IR active.
Charge Distribution
The molecule consists of two atoms of identical electronegativity, no net dipole moments are present.
N2 molecule
N2 molecule |
| N-N bond distance | 1.10550 Å |
| Calculation Type | FREQ |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| Charge | 0 |
| Energy(RB3LYP) | -109.524129 a.u., -287555.62 kJ/mol |
| RMS Gradient Norm | 0.00000060 a.u. |
| Imaginary Freq | 0 |
| Dipole Moment | 0.0000 Debye |
| Point Group | D∞h |
Item Value Threshold Converged?
Maximum Force 0.000001 0.000450 YES
RMS Force 0.000001 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000000 0.001200 YES
Predicted change in Energy=-3.400929D-13
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.1055 -DE/DX = 0.0
Data from calculations are found here
Vibrational Modes

Only symmetric stretch is present in N2 molecule in accordance with 3N - 5 rule for linear molecules. No net change of dipole moment occurs, and N2 is not IR active.
Charge Distribution
Like H2, no dipole moments are present, since it is a diatomic molecule with 2 atoms of identical electronegativity.
Thermodynamics of Haber Process
E(NH3)= -148492.43 kJ/mol
2*E(NH3)= -296984.86 kJ/mol
E(N2)= -287555.62 kJ/mol
E(H2)= -3094.25 kJ/mol
3*E(H2)= -9282.75 kJ/mol
ΔE = 2 X E(NH3)-[E(N2) + 3 x E(H2)] = -146.49 kJ/mol
ΔH Formation = 0.5 x {2 X E(NH3)-[E(N2) + 3 x E(H2)]}= -73.245 kJ/mol
The reaction is exothermic, implying that the products have a lower energy than the reactants. N2 has the lowest energy, making it the most stable compound among the reactants and products. However, this deviates from literature values of -45.94 kJ/mol. This deviation can be explained by the fact that energy calculated by the software does not take into account intermolecular interactions, and only analyses a single molecule. In reality, reactions have more complex intermolecular interactions such as dispersion forces in H2 and N2, along with hydrogen bonding in NH3 [3]
S2 Molecule
S2 molecule |
Description and Calculation
| S=S bond distance | 1.92943 Å |
| Calculation Type | FREQ |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| Charge | 0 |
| Energy(RB3LYP) | -796.32599779 a.u. |
| RMS Gradient Norm | 0.00000372 a.u. |
| Imaginary Freq | 0 |
| Dipole Moment | 0.0000 Debye |
| Point Group | D∞h |
Item Value Threshold Converged?
Maximum Force 0.000006 0.000450 YES
RMS Force 0.000006 0.000300 YES
Maximum Displacement 0.000011 0.001800 YES
RMS Displacement 0.000016 0.001200 YES
Predicted change in Energy=-7.077702D-11
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.9294 -DE/DX = 0.0 !
Data from calculations are found here
Vibrational Modes

In accordance with the 3N - 5 rule for predicting the number of vibrational modes for linear molecules, S2 has only one symmetric stretch present. No net change of dipole moment occurs for the symmetric stretch, and S2 is not IR active.
Charge Distribution
The molecule consists of two atoms of identical electronegativity, no net dipole moments are present.
Molecular Orbital Analysis
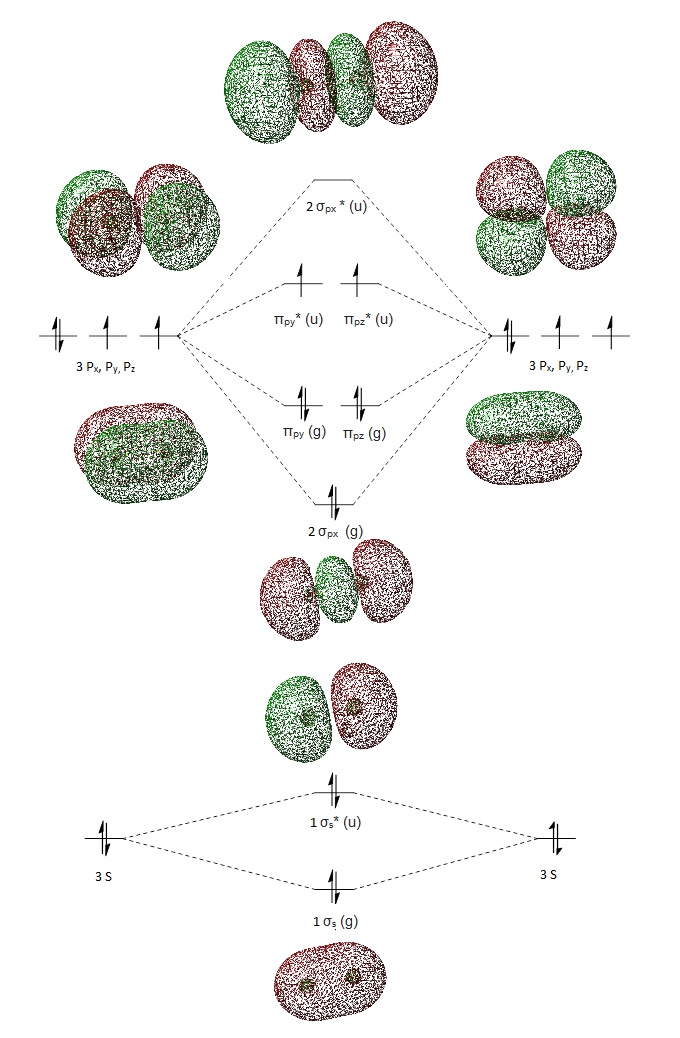
Bond order = 0.5 x (no. of bonding electrons - no. of anti-bonding electrons)
Bond order = 0.5 x (8 - 4) = 2
MO theory predicts a double bond, which is consistent with our expectations for S2 structure. The filled σ3px orbital is responsible for the S-S σ single bond. There are 4 electrons in the π orbital, and 2 electrons in the π* orbital. Overall, this leads to a π bond. Hence, a S=S bond is observed.

σ*3px orbital
- Energy: -0.01305 a.u.
- Anti-bonding orbital is caused by 3px orbitals combining out of phase
- Vacant orbital

LUMO π* Orbital
- Energy: -0.18463 a.u.
- LUMO is caused by 3pz orbitals combining out of phase
- Vacant Orbital
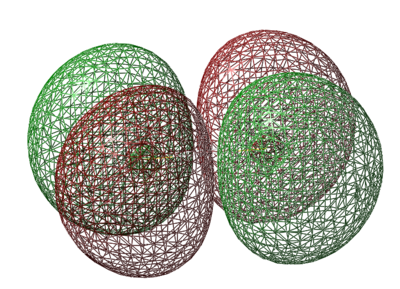
HOMO π* Orbital
- Energy: -0.21842 a.u.
- HOMO is caused by 3py orbitals combining out of phase
- Occupied Orbital
- In contrast to expectations that the 2 antibonding orbitals will be degenerate, 3pz and 3py have an energy gap according to calculations by Gaussian. If that is the case, the 2 π* Orbitals will not be singly filled, and instead, have 2 electrons in the HOMO. S2 will be diamagnetic, not paramagnetic, if this model is correct. However, this model could not separate the electron pair into 2 degenerate HOMOs, due to its imperfection as a model.
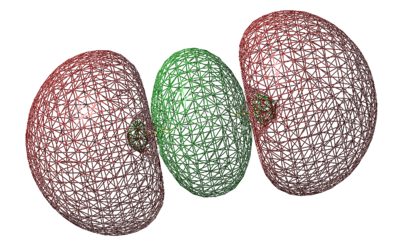
σ 3px orbital
- Energy: -0.39516 a.u.
- Bonding orbital is caused by 3px orbitals combining in phase
- Occupied orbital
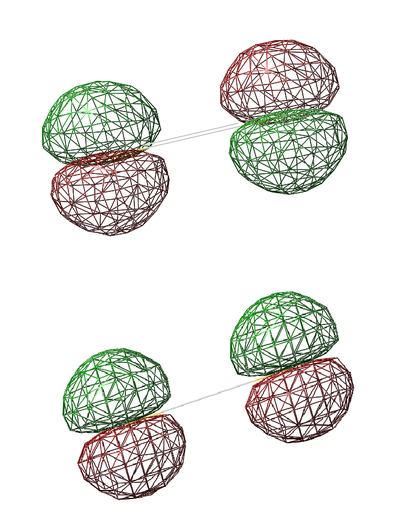
Non-Bonding 2p Orbitals
- Energy: -5.96349 a.u.
- The 2p orbitals are too far apart for bonding to substantially occur. Bonding occurs when atomic orbitals overlap at an optimal radius in the Leonard Jones Potential function where potential energy is at a minimum. This minimum cannot be reached due to the long S=S bond length that prevents effective overlap of 2p orbitals. Both 2p orbitals are degenerate, regardless of whether they are in phase or out of phase.
CH3OH
Ethanol molecule |
| Bond Length: O-H | 0.96520 Å |
| Bond Length: C-H | 1.1055 Å |
| Bond Length: C-O | 1.41811 Å |
| C-O-H bond angle | 107.737° |
| H-C-H bond angle | 108.258° |
| Calculation Type | FREQ |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d,p) |
| Charge | 0 |
| Energy(RB3LYP) | -115.72396437 a.u. |
| RMS Gradient Norm | 0.00001481 a.u. |
| Imaginary Freq | 0 |
| Dipole Moment | 1.6635 Debye |
| Point Group | N.A. |
Item Value Threshold Converged?
Maximum Force 0.000038 0.000450 YES
RMS Force 0.000020 0.000300 YES
Maximum Displacement 0.000307 0.001800 YES
RMS Displacement 0.000147 0.001200 YES
Predicted change in Energy=-1.416134D-08
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.093 -DE/DX = 0.0 !
! R2 R(1,3) 1.1006 -DE/DX = 0.0 !
! R3 R(1,4) 1.1006 -DE/DX = 0.0 !
! R4 R(1,5) 1.4181 -DE/DX = 0.0 !
! R5 R(5,6) 0.9652 -DE/DX = 0.0 !
! A1 A(2,1,3) 107.8995 -DE/DX = 0.0 !
! A2 A(2,1,4) 107.8995 -DE/DX = 0.0 !
! A3 A(2,1,5) 106.9041 -DE/DX = 0.0 !
! A4 A(3,1,4) 108.2583 -DE/DX = 0.0 !
! A5 A(3,1,5) 112.8278 -DE/DX = 0.0 !
! A6 A(4,1,5) 112.8278 -DE/DX = 0.0 !
! A7 A(1,5,6) 107.7374 -DE/DX = 0.0 !
! D1 D(2,1,5,6) 179.9999 -DE/DX = 0.0 !
! D2 D(3,1,5,6) 61.5463 -DE/DX = 0.0 !
! D3 D(4,1,5,6) -61.5465 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
Data from calculations are found here
Vibrational Modes
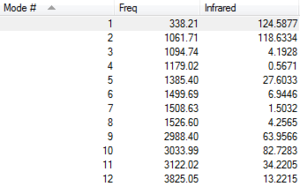
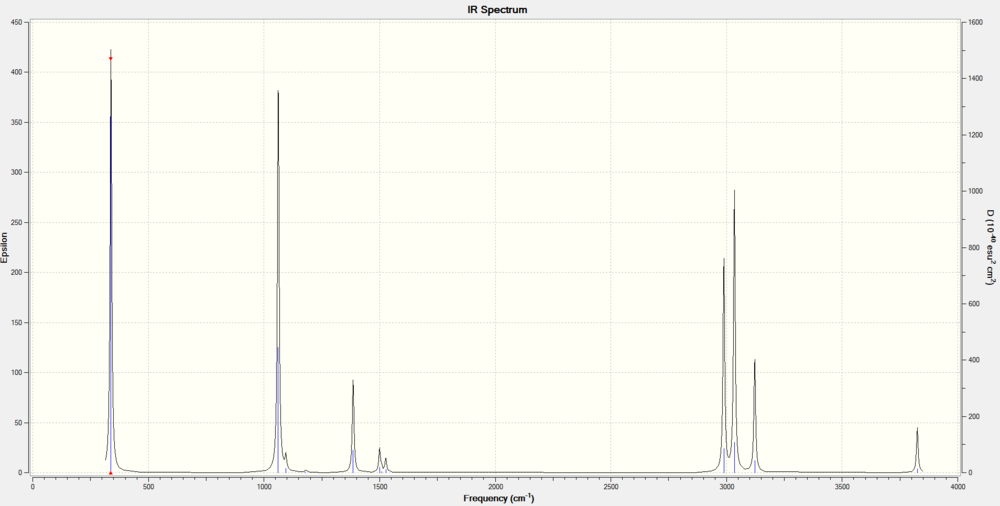
From the IR spectrum, the free O-H stretch is observed at 3825cm-1. This calculated value is higher than experimental values. C-H stretches are also observed at 2900-3100 cm-1 region. The C-O stretch is present at 1062 cm-1. The predicted peaks in the IR spectrum are in relative agreement with experimental data. [4]
Charge Distribution
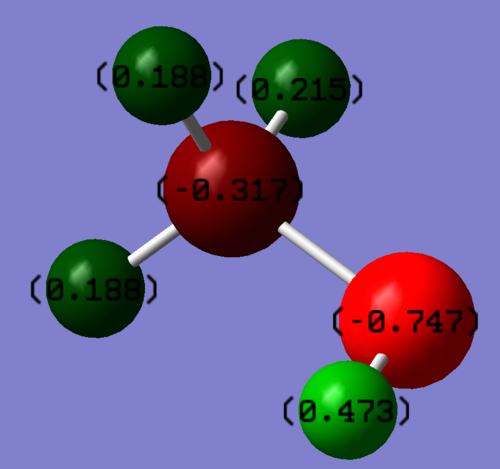
The oxygen atom is more electronegative than carbon and hydrogen, making carbon electron deficient, and hydrogen acidic.
Molecular Orbitals

Energy: 0.07706 a.u. The LUMO of methanol is a sigma anti-bonding orbital, σ*, predominantly between 3S orbital on Oxygen and 1S orbital on Hydrogen. As observed from the Molecular Orbital Coefficients(MO diagram too clustered), the orbital contribution from Hydrogen (MO coefficient = 1.21515) is greater than the orbital contribution from Oxygen(MO coefficient = -1.11893). This implies that the electrophilic site lies on the Hydrogen since a base or a nucleophile will penetrate the LUMO sigma anti-bonding orbital to abstract a Hydrogen from methanol. This is expected since Oxygen is more electronegative than Hydrogen, making methanol slightly acidic.
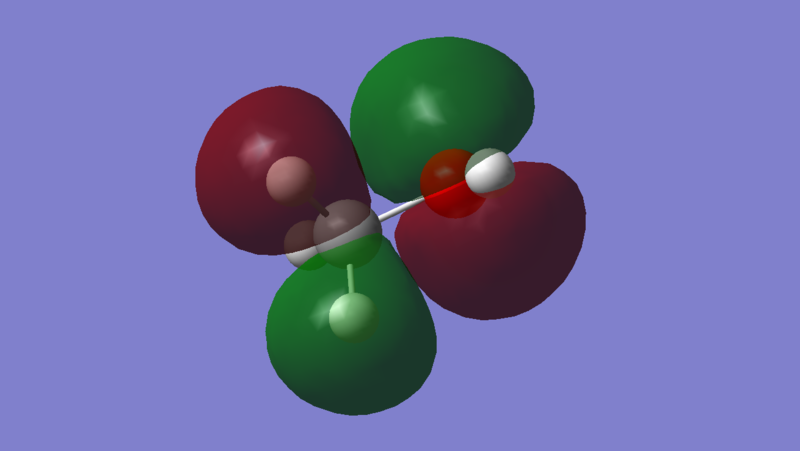
Energy: -0.26493 a.u. The HOMO of methanol is MO 9, and it is an anti-bonding π* orbital predominantly between 2Pz orbital carbon and 2Pz orbital oxygen. As observed by using the Molecular Orbital Coefficients, the orbital contribution from Oxygen (MO coefficient = 0.59487) is greater than the orbital contribution from Carbon (MO coefficient = -0.17875). This implies that the nucleophilic site lies on the oxygen, which is expected since oxygen is more electronegative than carbon. The p orbital of carbon is out of phase relative to the p orbital of oxygen.

Energy: -0.43327 a.u. The Pz orbitals of Carbon side on overlap with Pz orbitals of Oxygen, resulting in π bonding.
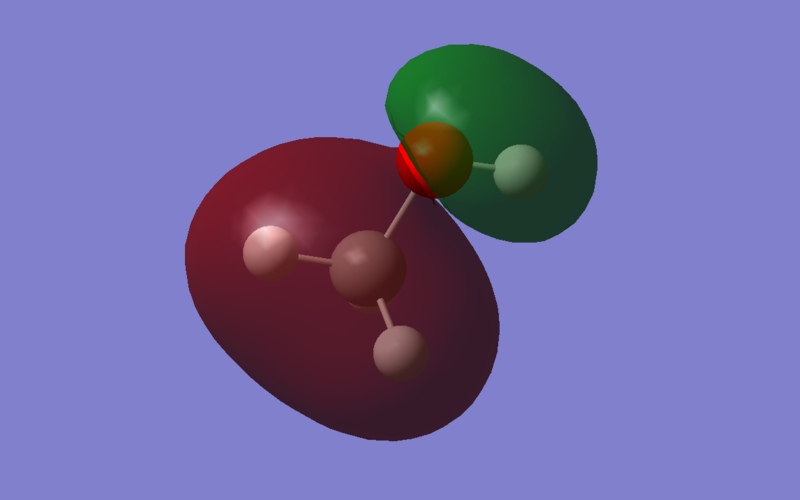
Energy: -0.67799 a.u. The S and P orbitals of Carbon overlap in phase with the 1s orbitals of Hydrogen, and the 2s orbitals of Oxygen overlap with the 1s orbitals of the alcoholic Hydrogen. However, The carbon orbitals and oxygen orbitals are out of phase. This is an anti-bonding σ* orbital.
Energy: -19.14032 a.u. The 1s orbitals of Oxygen are too low in energy to interact with the 1s orbitals of C or H.
References
- ↑ (2) Appl, M. Ullmann's Encyclopedia of Industrial Chemistry, 2006
- ↑ Bromberg, A.; Kimel, S.; Ron, A. Chemical Physics Letters 1977, 46, 262-266.
- ↑ Vanderzee, C.; King, D. The Enthalpies Of Solution And Formation Of Ammonia. The Journal of Chemical Thermodynamics 1972, 4, 675-683
- ↑ Plyler, E. Journal of Research of the National Bureau of Standards 1952, 48, 281
Cite error: <ref> tag with name "Ammonia" defined in <references> is not used in prior text.
