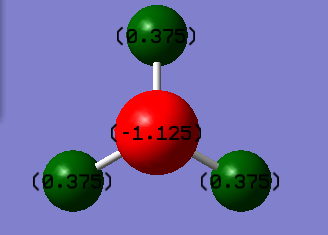
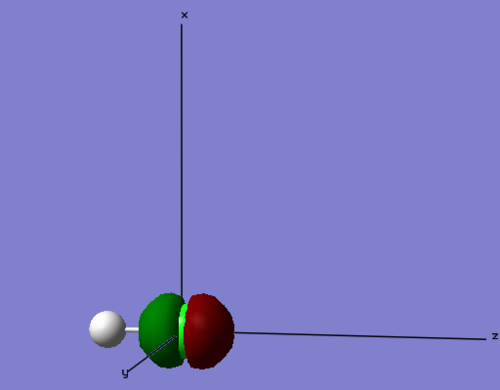
NH3 molecule

NH3

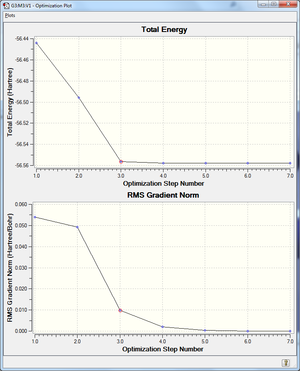
       Item               Value     Threshold  Converged?
Maximum Force            0.000000     0.000450     YES
RMS     Force            0.000000     0.000300     YES
Maximum Displacement     0.000000     0.001800     YES
RMS     Displacement     0.000001     0.001200     YES
Predicted change in Energy=-1.164080D-13

Specifications

H-N-H Bond angle - 105.74118

Bond distance - 1.01798Å

Calculation method - RB3LYP

basis set - 6-31G(d.p)

final energy E(RB3LYP): - 56.55 au

Point Group - C3V

RMS gradient - 0.00032440

Atom Chargesː

The file for the molecule is linked here

Molecule Vibrations

  FREQUENCY

1 1089.54

2 1693.95

3 1693.95

4 3461.29

5 3589.82

6 3589.82

how many modes do you expect from the 3N-6 rule?

N = 4. 3(4)-6 = 6. There will be 6 vibrational modes for NH3 according to this rule.

which modes are degenerate (ie have the same energy)?

1 and 2, and 4 and 6 have the same energy

which modes are "bending" vibrations and which are "bond stretch" vibrations?

1,2, and 3 represent bending vibrations; 4,5, and 6 are stretch.

which mode is highly symmetric?

4

one mode is known as the "umbrella" mode, which one is this?

1 - the molecule is inverted when it is bent

how many bands would you expect to see in an experimental spectrum of gaseous ammonia?

2 - only two IR active vibrations that result in a change in dipole moment.

Formation of Ammonia

Calculating the Energy Change

   E(NH3)= - 56.5576 a.u.
   2*E(NH3)= - 113.1152 a.u.
   E(N2)= -109.52412868 a.u.
   E(H2)= -1.15928020 a.u.
   3*E(H2)= 3.4778406 a.u.
   ΔE=2*E(NH3)-[E(N2)+3*E(H2)]= -0.1133594 a.u

= -297.6240772kj/mol

identify which is more stable, the gaseous reactants or the ammonia product?

The energy change is negative; the ammonia product has a lower energy than the gaseous reactants and hence is more stable.

confirm we have minimum and not a transition state structure.

The graph shows no negative curvature, therefore there will be no negative second derivative and a maximum will not exist, which would otherwise represent a transition state. The second derivative will hence only have a positive value, representing a minimum.

N2 MOLECULE

N2

Item                     Value       Threshold  Converged?
Maximum Force            0.000001     0.000450     YES
RMS     Force            0.000001     0.000300     YES
Maximum Displacement     0.000000     0.001800     YES
RMS     Displacement     0.000000     0.001200     YES
Predicted change in Energy=-3.401047D-13

Specifications

Bond distance - 1.10550Å

Atom Charges - 0

Bond Angle - 120 degrees

Calculation Method = RB3LYP

Basis Set = 6-31G(d,p)

E(RB3LYP) = -109.52412868 a.u.

RMS Gradient Norm = 0.00000060 a.u.

Point Group = D*H

The file for the molecule is linked to here

H2 MOLECULE

H2

The file for the molecule is linked to here

        Item               Value     Threshold  Converged?
Maximum Force            0.000708     0.000450     NO 
RMS     Force            0.000708     0.000300     NO 
Maximum Displacement     0.000934     0.001800     YES
RMS     Displacement     0.001321     0.001200     NO 
Predicted change in Energy=-6.251990D-07

Specifications

Bond distance - 0.600Å

Bond Angle - 120 degrees

Atom charges - 0

Calculation Method = RB3LYP

Basis Set = 6-31G(d,p)

E(RB3LYP) = -1.15928020 a.u.

RMS Gradient Norm = 0.09719500 a.u.

Point Group = D*H

HCL MOLECULE

HCL

        Item               Value     Threshold  Converged?
Maximum Force            0.000090     0.000450     YES
RMS     Force            0.000090     0.000300     YES
Maximum Displacement     0.000139     0.001800     YES
RMS     Displacement     0.000197     0.001200     YES
Predicted change in Energy=-1.270754D-08
Optimization completed.
   -- Stationary point found.

Specifications

Bond distance - 1.28599Å

Bond Angle - 120 degrees

Calculation Method = RB3LYP

Basis Set = 6-31G(d,p)

E(RB3LYP) = -460.80077875 a.u.

RMS Gradient Norm = 0.00005211 a.u.

Dipole Moment = 1.4334 Debye

Point Group = C*V

Charges:

The file for the molecule is linked to here

Molecular Orbitals HCʟ

This shows the unoccupied molecular orbital possessing the lowest energy (LUMO) for the HCL molecule.

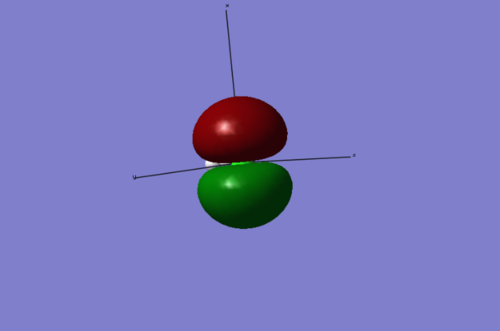This shows the degenerate 3px HOMO on the chlorine atom. Interestingly, in this case neither of the Highest Occupied Molecular Orbitals are bonding orbitals.

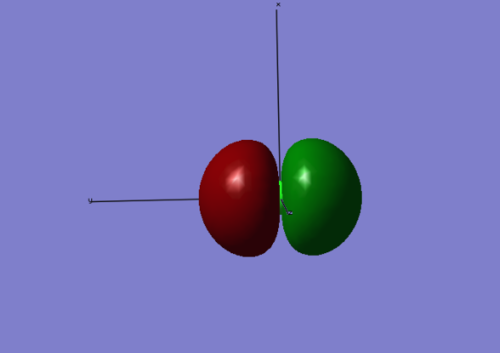This shows the degenerate 3py HOMO. Again, it is a non-bonding orbital.

This shows the sp molecular orbital formed with the 1S electron on the Hydrogen atom and the 3p electron on the Chlorine.

These illustrate further degeneracy in the 3px and 3py orbitals of the clorine atom, illustrated by the directionality of the orbital with respect to the cartesian axis'; both orbitals have the same solution to the schrodinger equation of 7.22836, and hence the same energy.

However, the pz orbital shows a slightly higher solution of 7.23847 despite the atomic orbitals being degenerate for npx, npy, and npz; it is likely interactions with the Hydrogen 1s orbital in the z plane raise the orbitals energy slightly.