User:Xx108 (module 1)

Module 1

The basic techniques of molecular mechanics and semi-empirical molecular orbital methods for structural and spectroscopic evaluations

Modelling using Molecular Mechanics

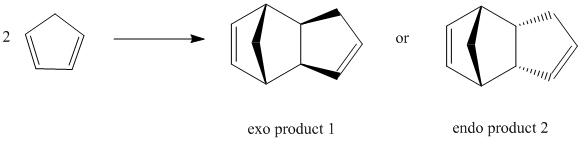
Dimerisation of cyclopentadiene

Results obtained after using the MM2 force field options

	stretching / kcalmol-1	bending / kcalmol-1	tortion / kcalmol-1	van der Waals / kcalmol-1	dipole-dipole / kcalmol-1	total energy / kcalmol-1
exo dimer	1.2856	20.5790	7.6571	4.2324	0.3776	31.8766
endo dimer	1.2507	20.8477	9.5109	4.3194	0.4476	33.9975

According to the above table, the exo dimer has a total energy of 31.8766kcal/mol while the endo dimer has a total energy of 33.9975kcal/mol. This shows that the exo dimer is the thermodynamic product(lower in energy,more stable) whereas the endo dimer is the kinetic product(higher in energy,less stable). For this Diels-Alder dimerisation process, the endo dimer(kinetic product) is formed, which is mainly due to the secondary p orbital interactions between two cyclopentadiene molecules. In addition, the kinetic product(endo dimer)is favoured because it has a lower energy barrier to overcome compared to that for the thermodynamic product(exo dimer).

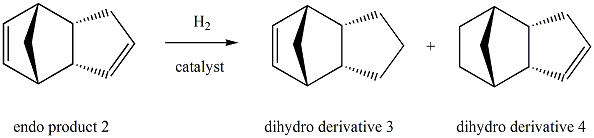
The hydrogenation of cyclopentadiene dimer

Results obtained after using the MM2 force field options

	stretching / kcalmol-1	bending / kcalmol-1	tortion / kcalmol-1	van der Waals / kcalmol-1	dipole-dipole(hydrogen bonding) / kcalmol-1	total energy / kcalmol-1
dihydro derivative 3	1.2777	19.8661	10.8068	5.6329	0.1621	35.6850
dihydro derivative 4	1.0958	14.5234	12.4979	4.5123	0.1406	31.1520

The total energy for the dihydro derivative 4(31.1520kcal/mol) is lower compared to that for the dihydro derivative 3(35.6850kcal/mol). This indicates that the dihydro derivative 4 is the thermodynamic product while the dihydro derivative 3 is the kinetic product. As a consequence, formation of product 4 is thermodynamically more favourable and the dihydro derivative 4 is the major product. The difference in total energy(4.53kcal/mol) is mainly accounted for by the difference in bending energy(5.34kcal/mol). This is because the bond angle for product 3(108.2⁰) deviates more from the typical sp² hybridised carbon framework than that for product 4(112.4⁰), resulting in a larger bending energy for product 3.

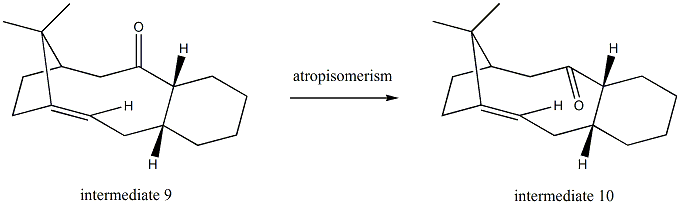
Stereochemistry and reactivity of an intermediate in the synthesis of Taxol

Results obtained after using the MM2 force field options

	stretching / kcalmol-1	bending / kcalmol-1	tortion / kcalmol-1	van der Waals / kcalmol-1	dipole-dipole / kcalmol-1	total energy / kcalmol-1
isomer 9 chair conformer	2.6837	15.8108	18.1324	12.6057	0.1172	48.7721
isomer 9 boat conformer	2.8439	16.6597	21.4216	14.1854	0.1480	54.9428
isomer 10 chair conformer	2.5140	10.6902	19.6076	12.5587	0.1813	44.3379
isomer 10 boat conformer	2.6533	11.1325	22.9481	13.8626	0.1738	49.9453

For both isomer 9 and isomer 10, the total energy is minimized when the cyclohexane ring is in a chair conformation. Since the chair conformer of isomer 9 has a total energy of 48.7721kcal/mol while the chair conformer of isomer 10 has a total energy of 44.3379kcal/mol, isomer 10 is thermodynamically more stable.

This kind of alkene(hyperstable alkene) is very difficult to undergo hydrogenation simply because it is less strained than the corresponding alkane,which makes it become very unreactive.

Results obtained after using the MMFF94 field method

	total energy / kcalmol-1
isomer 9 chair conformer	70.5536
isomer 10 chair conformer	60.5774

Unlike the MM2 method, the cyclohexane ring is changed automatically to the more stable chair conformation during the minimization process under MMFF94 method. Therefore, only the total energy for the chair conformer of both compounds is shown. The result is consistent with that obtained using MM2. Isomer 10 is again proved to be more stable as its total energy is lower.

Modelling usig semi-empirical molecular orbital theory

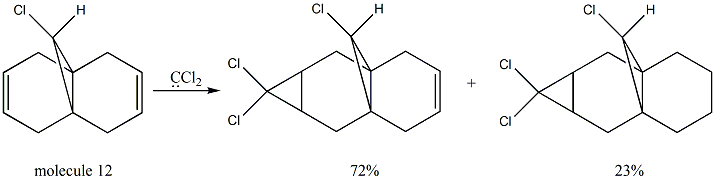
Regioselective addition of dichlorocarbene

Part 1

Different molecular orbitals for molecule 12

LUMO+2	LUMO+1	LUMO	HOMO	HOMO-1

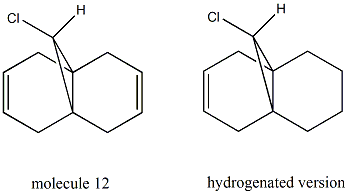
From the MM2 method, the total energy of molecule 12 is minimized to 17.8945kcal/mol. After this, the MOPAC/PM6 method is applied in order to provide a representation of the valence-electron molecular wavefunction. From the pictures above, it can be seen that the electorn density is higher around the syn C=C bond than the anti C=C bond in the HOMO and HOMO-1 orbitals. Therefore, the syn C=C bond is more nucleophilic than the anti C=C bond and is more likely to undergo an electrophilic addition reaction. Since the reaction with dichlorocarbene is analogous to electrophilic addition, this method does discriminate between the two alkene bonds. What's more, the molecule 12 itsself has a plane of symmetry but the molecular orbitals shown are unsymmetrical. This is probably due to the limitations of the MOPAC/PM6 method used and it can be improved by introducing an alternative method.

Part 2

Results summarized from the IR spectra of both compounds

	C-Cl stretch	syn C=C stretch	anti C=C stretch
molecule 12	771.82cm-1	1756.24cm-1	1738.66cm-1
hydrogenated version	777.82cm-1	1759.14cm-1	-

From the above table, we can see that the C-Cl stretches for both compounds are in good agreement with the literature (740-780cm^-1) and C=C stretches are slightly higher compared to the literature value (1620-1680cm^-1). In addition, a larger value od C-Cl stretch is observed for the hydrogenated compound compared to that for molecule 12. After hydrogenation, the interaction between the anti C=C pi orbital and C-Cl sigma* orbital vanishes. In this way, the electrons donated into the anti-bonding orbital of C-Cl bond are fewer, leading to a longer bond length and hence a weaker C-Cl bond.

Monosaccharide chemistry: glycosidation

Results obtained after using both the MM2 and MOPAC/PM6 methods

	stretching / kcalmol-1	bending / kcalmol-1	tortion / kcalmol-1	van der Waals / kcalmol-1	dipole-dipole / kcalmol-1	total energy / kcalmol-1	Heat of formation / kcalmol-1
A	2.4331	13.9045	-3.2516	17.7430	7.8624	30.2583	-78.4023
A'	2.2607	12.5835	-4.1634	17.4102	6.5319	34.2548	-73.2374
B	2.5140	13.8565	-1.5187	17.5266	7.1408	38.2059	-73.9246
B'	2.2375	11.3798	-2.2316	16.4670	6.2301	32.3412	-67.7125
C	2.0942	17.4346	3.4250	16.1736	1.2481	33.0317	-78.7253
C'	4.2491	23.7328	5.1734	18.0368	0.7732	47.2654	-65.1094
D	2.0112	22.4795	-2.1766	14.5730	4.9241	30.6234	-74.3058
D'	2.6781	19.8349	5.2546	17.8437	4.0372	44.2738	-61.2453

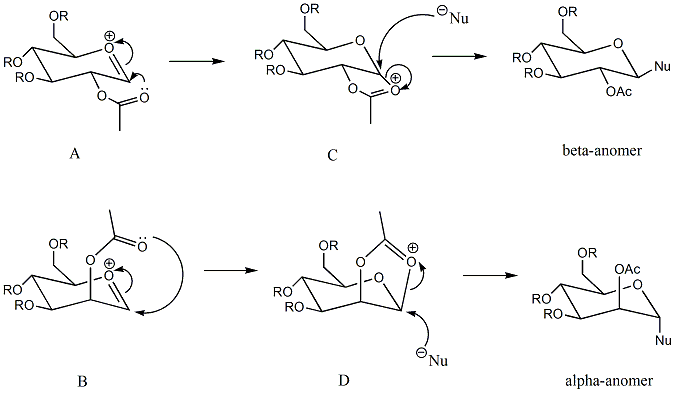
Methyl group is the appropriate R group since it is the smallest one among all the alkyl groups. In this way, the computational demand will be kept at a minimum. Heretwo different methods are used to exmaine the neighbouring-group-participation. Since neighbouring-group-participation is caused by the interaction between the oxygen on -OAc group and the sigma* orbital on C=O⁺ which has a quantum mechanical nature, the MM2 method may not be suitable for this task. Instead, the MOPAC/PM6 method is able to detect this kind of interaction, giving a better result.

As discussed above, MOPAC/PM6 is the more appropriate method. Therefore, when deciding which one of the pairs(A/A' and B/B') has the lower energy, only the results obtained from the MOPAC/PM6 method should be used. The one with a more negative heat of formation value will be more stable.

Similarly the two methods have been used to obtain values for the intermediates C and D as well. According to the heat of formation data, C'/D' is very unstable compared to C/D. In contrast, A'/B' is just slightly unstable comapared to A/B. This shows that C and D predominate in this reaction and it has been approved by literature. As a consequence, it is no longer possible to get two isomers, the reaction is stereospecific.

Structure based mini project using DFT-based molecular orbital methods

Stereoselective dissolving metal reductions

Results obtained from ¹³C NMR spectrum for alcohol 6 and comparison with the literature

	carbon 1	carbon 2	carbon 3	carbon 4	carbon 5	carbon 6	carbon 7	carbon 8	carbon 9	carbon 10	carbon 11	carbon 12	carbon 13	carbon 14	carbon 15
chemical shift calculated/ppm	74.36	42.15	40.81	33.73	41.29	30.62	24.07	38.94	25.76	38.14	33.02	150.83	105.01	23.88	15.24
chemical shift from the literature/ppm	76.83	38.82	43.35	33.48	39.93	30.95	16.88	37.31	24.57	39.19	27.35	148.25	111.76	22.49	14.72
absolute difference	-2.47	3.33	-2.54	0.25	1.36	-0.33	7.19	1.63	1.19	-1.05	5.67	2.58	-6.75	1.39	0.52
percentage difference	-3.2%	8.6%	-5.9%	0.7%	3.4%	-1.1%	42.6%	4.4%	4.8%	-2.7%	20.7%	1.7%	-6.0%	6.2%	3.5%

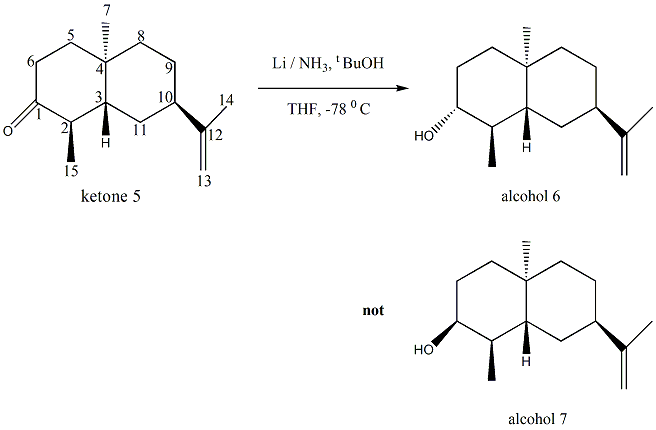
By comparing the IR spectra for both the reactant and the product, it should be able to tell whether the reaction works or not. This is because in ketone 5, there is a strong peak at about 1680cm^-1 due to the presence of carbonyl group. In contrast, In either alcohol 6 or alcohol 7, this carbonyl peak will disappear and there will be a broad peak for the -OH group at 3600cm^-1. By working out both the sign and magnitude of the optical rotation value, it should be possible to distinguish between the two stereoisomers, namely alcohol 6 and alcohol 7.

From the tabulated results shown above, it can be concluded that the predicted ¹³C NMR data generally match the reported. The only two exceptions are the values for carbon 7(42.6% difference) and carbon 11(20.7% difference). The others are in good agreement with the literature(all within a 9% difference).

Results obtained from the MOPAC/PM6 method

	heat of formation(kcal/mol)
alcohol 6	-84.45
alcohol 7	-85.31

Alcohol 6 is formed rather than alcohol 7 mainly because of the issue of steric hindrance. When the ^tBuOH comes towards ketone 5, it will attack from the top face of the molecule because it is sterically less hindered. Despite the fact that the thermodynamic product is usually formed in the dissoving metal reductions of cyclohexanone, here the less stable alcohol 6(heat of formation = -84.45kcalmol^-1) is formed simply because it is under kinetic control.