00554846 Org1

Modelling with the use of Molecular Mechanics

Introduction

The exercise carried out in this module involves the calculation of energies and properties of reactions like the hydrogenation of the cyclopentadiene dimer, and also focuses on several molecules that are experimented on computationally here. Using molecular mechanics circumvents the calculation of particular values of energies based on the Schrodinger equation, and instead models the value based on the equation itself. The modelling is done by means of separating the properties of the molecules into different calculable functions that succinctly describe bond properties as a whole.

The calculable functions are equations that specifically regard the interactions between molecules, and these can be seen as follows:

The sum of all diatomic bond stretches, where it is based on a Hookes' law potential: $\sum _{\mathrm{b}\mathrm{o}\mathrm{n}\mathrm{d}\mathrm{s}}{K}_r(r-r_{eq}{)}^2$

The sum of all triatomic bond angle distortions: $\sum _{\mathrm{a}\mathrm{n}\mathrm{g}\mathrm{l}\mathrm{e}\mathrm{s}}{K}_{\theta }[(\theta -{\theta }_{eq}{)}^2]$

The sum of all the dihedral terms, which describes the torsion around the bond: $\sum _{\mathrm{d}\mathrm{i}\mathrm{h}\mathrm{e}\mathrm{d}\mathrm{r}\mathrm{a}\mathrm{l}\mathrm{s}}\frac{V_N}{2}[1+\mathrm{c}\mathrm{o}\mathrm{s}(N\varphi -\gamma )]$

The sum of all the non-bonded electrostatic (either attractive or repulsive) and Van der Waals repulsions: $\sum _{\mathrm{n}\mathrm{o}\mathrm{n}\mathrm{-}\mathrm{b}\mathrm{o}\mathrm{n}\mathrm{d}\mathrm{e}\mathrm{d}}[\frac{A_{ij}}{R_{ij}^{12}}-\frac{B_{ij}}{R_{ij}^6}+\frac{q_i{q}_j}{ϵR_{ij}}]$

The aformentioned functions are solved with the use of known parameters that have been derived experimentally, and the solutions subsequently added together to give the steric energy of a molecule.This modelling is based on the MM2 programme formulated by N. L. Allinger in the 1970s, and various improvements have been made to the programme thus far. For the molecular modelling carried out in this module, the MM2 programme can give a reliably good approximation of simple organic molecules, but unfortunately discounts the electronic factors that come into play in a molecule, and also the importance of orbital overlap is not taken into account here. Additionally, the deriving of the experimentally derived constants in the equation ($K_r,K_{\theta }$, etc.) stems from the bonds of simple diatomic molecules and hence the modelling used in these experiments are best suited for simple molecules.

The Hydrogenation of the Cyclopentadiene Dimer

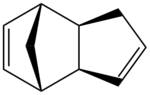
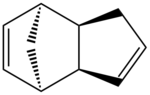
Dimerisation of Cyclopentadiene through a Diels-Alder cycloaddition

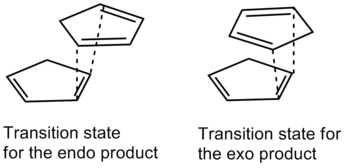
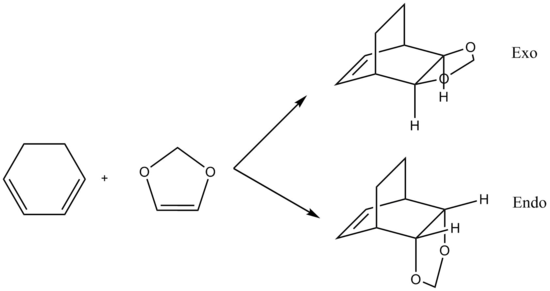
Cyclopentadiene dimerises at room temperature according to the Diels-Alder mechanism, giving rise to the endo and exo products which can be seen in table 1.

Using the programme ChemBio3D, the relative energies of the endo and exo products that results from the dimerisation of cyclopentadiene can be calculated. These calculations are based on the MM2 techniques outlined above with the equations. Here, the exo product is seen to have an energy of 31.8834 kcal/mol, whilst the endo product has an energy of 34.0080 kcal/mol. Examining the diagrams and comparison of the energies calculated by the programme allows for a further rationalisation of why the energy for the endo mode is higher than that of the exo mode.

Table 1: Comparison of the Energies of Products Exo 1 and Endo 2

Contribution	Exo Product 1	Endo Product 2	Energy Difference
Image
3D Image
Stretch	1.2923	1.2463	0.046
Bend	20.587	20.8773	-0.2903
Stretch-Bend	-0.8413	-0.8321	-0.0092
Torsion	7.6715	9.5038	-1.8323
Non-1,4 VDW	-1.4358	-1.5266	0.0908
1,4 VDW	4.342	4.2938	0.0482
Dipole/Dipole	0.3778	0.4454	-0.0676
Total Energy	31.8834	34.008	-2.1246

In table 1, it can be observed that there are more dominant contributions from the bend and torsion which are the energies that largely contribute to the system strain. It should then be logically concluded that the exo product of the dimerisation should be the major product. However, the endo product is the major product of the dimerisation instead and this can be rationalised by the fact that the transition state of the endo product is less sterically hindered compared to that of the exo product's. Additionally it can be observed from table 1 that the energies with the greatest differences is due to the torsional energy which causes the twisting of the bonds in the endo product, raising the energy of the endo product relative to the exo product. The MM2 method therefore predicts the exo to be the major product, which is wrong as it only minimises the energy but fails to include the consideration of the reaction path taken - the transition states.

With the two facts about the endo product, it can be concluded that the endo product is the thermodynamic product of the reaction whereas the exo product is the kinetic product.

Hydrogenation of the endo product

From the endo product of the dimerisation, the following hydrogenation will result in either product shown in the diagram below:

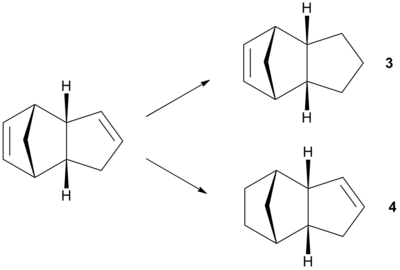
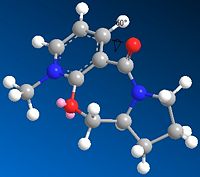
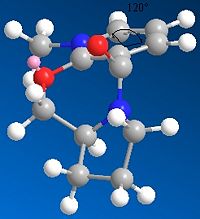
From the calculations carried out of ChemBio3D, it can be seen that the total energy for molecule 3 is higher than that of molecule 4's.

Table 2: Comparison of the Energies of Products 3 and 4

Contribution	Hydrgenated Product 3	Hydrogenated Product 4	Energy Difference
3D Image
Stretch	1.2817	1.0824	0.1993
Bend	19.8562	14.5053	5.3509
Stretch-Bend	-0.8365	-0.5447	-0.2918
Torsion	10.8077	12.5117	-1.704
Non-1,4 VDW	-1.2165	-1.0433	-0.1732
1,4 VDW	5.6323	4.5126	1.1197
Dipole/Dipole	0.1622	0.1407	0.0215
Total Energy	35.687	31.1647	4.5223

From table 2, it can be observed that the hydrogenated product 3 has an overall higher energy compared to the product 4. This can be explained by the fact that for the molecule 3, the bending energy is quite significant, due to the fact that the bond angle for the alkene bending is 107.6^o, different from the predicted angle for a free alkene at 120^o. In contrast, the bond angle for the alkene bending is 112.4^o, closer to the predicted angle bending for a free alkene. Therefore there will be a lower contribution from the bending energy to the overall energy of molecule 4.

It can be concluded from table 2 that molecule 4 has an overall lower energy of the two, which implies that the double bond in the cyclohexene component of the dimer is easier to hydrogenate.

Stereochemistry of the Nucleophilic Additions to a Pyridinium Ring (NAD⁺ analogue)

For the two reactions to be studied below, the molecules 5 and 6 featured is an optically active prolinol derivative. This reaction has been reported by Schultz and Flood to be a highly enantioselective and regioselective reaction, giving ee% of up to 98. This selectivity is pertains particularly to the addition of the methyl group anti to the hydrogen molecule bending away from the plane of the page.

Prolinol 5

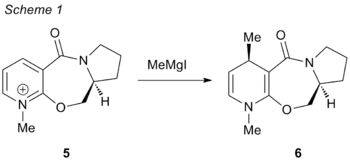
The mechanism of the reaction can be seen in scheme 2, where the nucleophile approaches the substrate molecule from the top face to give the desired product 6. This selectivity is due to the Grignard reagent's (MeMgI) coordination to the carbonyl, which then causes the approach of the Me^- species to be only from one direction. Therefore, it is an imperative that the dihedral angle of the carbonyl bond relative to the pyridine ring be taken into consideration.

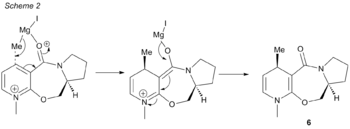
The position of the carbonyl could be in two particular conformations; one above the plane of the 7-membered ring, or below the plane of the 7-membered ring. This could lead to two different results; one with the inclusion of the Me out of the plane of the page, as seen for molecule 6, or with the Me below the plane of the page. The enantioselectivity of the reaction can be investigated with the use of modelling with molecular mechanics by making slight tweaks to the conformation, such that the dihedral angle between the carbonyl and aromatic ring and the energies of the two molecules can be compared.

As aforementioned, the MM2 programme is unable to recognize and do accurate modelling for metals like Mg, and hence the Grignard reagent is not included in the calculation for the minimising of energies. Only simple diatomic interactions and atoms (e.g. C, N, O, H, S, F, Cl, Br, I) can be recognized by the programme. As a result, only the substrate was minimised by fixing the dihedral angle between the carbonyl and the aromatic ring, and then minimising the conformation. The results of varying the dihedral angle can be seen in the table below:

Table 3: Comparison of the different conformations

Conformer	Dihedral Angles/o	Energy/kcalmol-1
1	-120	75.2563
2	-90	77.0257
3	-60	62.0535
4	-11.3897	45.5198
5	0	43.7762
6	5	43.2916
7	9.7101	43.1093
8	60	57.2655
9	90	71.0453
10	120	76.2406

From literature, the suggestion that only two conformation minima are possible is confirmed by the data in table 3, for which the conformations 5, 6 and 7 have the lowest energy. The two conformations will therefore be when the carbonyl is above the plane of the ring, anti to the hydrogen atom at the chiral centre, and when the carbonyl is in the same plane as the pyridine ring. Additionally, conformations with the carbonyl below the ring and with dihedral angles larger than those of conformations 5, 6 and 7 are not stable enough for isolation, as suggested by the data in table 3.

On further examination of the dihedral angles of conformations 6 and 7, it can be concluded that even the small dihedral angles ranging from 5-9.7^o can give rise to the selectivity in the reaction outlined in scheme 2. The conformation with the dihedral angle of 9.7^o possessed the lowest energy and is hence the most stable. The probability that the Grignard reagent will find the molecule 6 in conformation 7 is the highest. Further elaboration on the differences between the energy contribution to the final energy of the conformations, including the diagrams and models can be seen in table 4.

Table 4: Comparison of the different conformations

Conformer	7	8	10
3D Image
Dihedral Angle	9.7101	60	120
Stretch	2.0462	2.0032	2.0213
Bend	14.2583	12.5212	17.7753
Stretch-Bend	0.13	0.109	0.1668
Torsion	5.0484	24.294	41.379
Non-1,4 VDW	-0.5147	-2.5147	-2.5015
1,4 VDW	16.5633	15.3321	15.2156
Charge/Dipole	9.5879	9.4428	6.1404
Dipole/Dipole	-4.0102	-3.9219	-3.9563
Total Energy	43.1093	57.2655	76.2406
JMol

The models of the three conformations allow for the easy visualisation of the coordination of the Grignard reagent to the carbonyl oxygen from beneath the carbonyl, and therefore, the methyl species will attack the carbon centre from the above plane with respect to the pyridine ring so that a steric clash can be avoided with the H of the target carbon. As a result, the chiral product 6 is synthesised in the dominant ratio compared to its enantiomer.

Prolinol 7

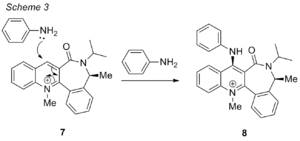
Similarly, the reaction of molecule 7 with aniline was modelled by varying the dihedral angle of the carbonyl against the planar pyridine ring. However, the reagent is aniline instead of the Grignard Reagent, and this reaction involves the substitution of the PhNH² nucleophile onto the meta position on the pyridine ring. With reference to literature, it shows that the incoming nucleophile will attack from the face of the plane opposite to the plane that the C=O group is in, leading to a high enantioselectivity in the product, and antropenantioselectivity, where addition is carried out selectively in one face. As a result of this, the 1,4 adducts formed in the reaction are known as chiral nucleophilic transfer reagents. This reaction can also be carried out on other functional groups like cyanides and enolates. In this section, MM2 modelling was used to understand these results.

A summary of the mechanism for the reaction can be seen in scheme 3:

A table of results are shown, with varying dihedral angles between the C=O group and the pyridine ring

Table 5: Comparison of the different conformations

Conformer	Dihedral Angles/o	Energy/kcalmol-1
1	-16.6	63.8221
2	16.6	70.4551
3	50	88.3024
4	-50	68.8267

From table 5, the position where the carbonyl is below the plane (negative value of the dihedral angle) of the pyridine ring is favoured energetically over the conformer where it contains the same dihedral angle in the opposite plane. This is due to the fact that the methyl and isopropyl groups point upwards in the molecule, and hence to prevent a steric clash the carbonyl group will have to point downwards. The target molecule is sterically hindered in specific areas, and consideration of the nucleophile PhNH₂ comes to the conclusion that the phenyl ring is very bulky and hence it will approach the target molecule in a certain direction. The combination of these two factors leads to the conclusion that the approach of the nucleophilic nitrogen will avoid the oxygen on the carbonyl due to the presence of lone pairs on both these atoms. Therefore the nucleophile will approach the target molecule from the opposite plane where the carbonyl is sterically situated, which is as aforementioned below the plane of the pyridine ring. The table illustrates the stability of the conformers with different dihedrals, and the conformer with the negative dihedral angle - representing a positioning of the carbonyl below the plane of the pyridine ring - has the lower energy, therefore it is more stable.

Table 6: Comparison of conformations 1 and 2

Conformer	1	2
3D Image
Dihedral Angle	-16.6	16.6
Stretch	4.1416	4.4469
Bend	12.228	15.1877
Stretch-Bend	0.4237	0.4242
Torsion	8.9696	11.908
Non-1,4 VDW	4.4565	4.6795
1,4 VDW	29.3922	29.6029
Charge/Dipole	9.0807	9.0954
Dipole/Dipole	-4.8702	-4.8896
Total Energy	63.8221	70.4551
JMol

Furthermore, on examination of the product energies as a result of attacks from the plane above and below the pyridine ring confirms that the attack from the top plane of the target molecule is highly favoured to give a more stable product. This is proven by the vast difference in the energies of the product molecules due to different modes of attack. Therefore, the outcome of this reaction is opposite to that of the reaction involving the prolinol 5.

Table 7: Comparison of Products due to different modes of attack from the nucleophile

Product	Attack above the plane	Attack below the plane
3D Image
Stretch	4.2375	8.6269
Bend	18.6769	121.1446
Stretch-Bend	0.8176	0.3813
Torsion	5.0272	6.5321
Non-1,4 VDW	2.1578	8.5665
1,4 VDW	33.9493	45.0567
Dipole/Dipole	-6.7612	-5.9794
Total Energy	58.105	184.3286
JMol

Finally, the addition of two molecules in the model window in the MM2 program will cause results to vary widely from that of literature, and hence other programs such as MOPAC could be utilised to bring about more accurate values as other factors like the molecular orbitals of the target molecule and nucleophile are taken into account and will definitely bring about a more accurate value.

Stereochemistry and Reactivity of an Intermediate in the Synthesis of Taxol

Examination of the Intermediates 9 and 10

For the total synthesis of Taxol, the intermediates 9 and 10 are essential, and hence their synthesis is of great interest in the research circles. Paquette and co-workers have suggested that the synthesis of Taxol using these intermediates begin with the carbonyl group facing either up or down, as shown in the diagram below.

Intermediates 9 and 10 are known to isomers of each other, particularly known as atropisomerism. For this case, intermediate 9 characteristically isomerises into intermediate 10, which is proven with the use of MM2 molecular modelling.

Table 8: Comparison of the energies of the isomers

	Conformer 9	Conformer 10 (chair)	Conformer 10 (twist-boat)
3D Image
Stretch	3.1891	2.5491	2.6622
Bend	20.4625	10.7172	11.4817
Stretch-Bend	0.4968	0.3243	0.3143
Torsion	21.8336	19.5975	21.5635
Non-1,4 VDW	-0.6421	-1.2539	-1.1781
1,4 VDW	14.4209	12.5436	13.5782
Dipole/Dipole	0.0034	-0.1824	-0.1934
Total Energy	59.7642	44.2954	48.2283
JMol

From table 8, it can be observed that the formation of the intermediate 10 is favoured due to its lower energy, and hence when a solution containing both intermediates are left at room temperature, the isomerisation of intermediate 9 to 10 is favoured. This leads to the conclusion that the formation of the intermediate 10 is under a thermodynamic driving force, leading to its favoured formation at room temperature. Additionally, the favoured formation of the C=O below the plane of the pyrdinium ring can be due to the fact that the C=O above the plane of the pyridinium ring causes the locking of the cyclohexane ring in the sterically unfavourable twist boat conformation. This reason, coupled with the unfavourable interactions with neighbouring hydrogen atoms flanking the sides of the C=O causes the energy of the intermediate 9 to be the highest.

In addition to the formation of the intermediate 10, there are two possible conformations of conformation 10, one of which contains the cyclohexane ring in a chair conformation whilst the other has the ring in a twist-boat conformation. The hexane ring in focus is highlighted in blue, which allows for the observation of the chair and twist boat conformations in the intermediate. For the intermediate 10 containing the chair conformation, it was proven to be more stable as it possessed less energy compared to the twist-boat conformation by 3.9 kcalmol^-1. The favouring of the chair conformation can be largely attributed to the higher steric clash resulting from the boat conformation, as compared to the chair conformation which minimises the amount of steric clash in the system.

The conclusion that the intermediate 10, containing cyclohexane in the chair conformation is the most stable. Therefore, if a nucleophilic reaction were to be carried out under thermodynamic conditions, the product that results from the intermediate 10 (chair conformation) would be the major product due to its favoured formation.

Table 9: Comparison of energies from MM2 and MMFF94

Conformer	MM2	MMFF94
9	59.7642	82.7234
10 (chair)	44.2954	60.5833
10 (twist-boat)	48.2283	66.3803

Finally, in table 9, it can be seen that optimisation carried out on the MMFF96 programme results in higher absolute values for the energies of the intermediates. However, the MMFF94 also predicts correctly the most stable intermediate out of the three possible conformations, which is in line with the values acquired from the MM2 program.

Hyperstable Alkenes

The hydrogenation product of the lowest energy intermediate mentioned in the section above was modelled and gave a higher energy value of 53kcalmol^-1. The breakdown of energies can be seen in table 10.

Table 10: Energy of the hydrogenated product

Energy Contribution /kcalmol-1	Energy /kcalmol-1
3D Image
Stretch	2.8237
Bend	13.6385
Stretch-Bend	0.6579
Torsion	21.9436
Non-1,4 VDW	-1.4975
1,4 VDW	15.4395
Dipole/Dipole	0.0000
Total Energy	53.0055
JMol

From the table above, it can be observed that the final energy of the product is higher than that of the intermediate alkene. This would imply that the formation of the product is not very favourable, and this can be attibuted to the hyperstable properties of the alkenes. It has been discovered by Schleyer and co-workers that the formation of bridgehead olefins such as intermediate 10 causes it to be hyperstable. This is due to the strain associated with the double bond of the alkene, which is much less than that of the strain associated with the alkane also involving a bridgehead. In the energetical calculations carried out, the strain can be evaluated through the olefin strain energies (OS), known as the torsion in the MM2 calculations. In the values obtained, the torsion of the hydrogenated product is 21.94 kcalmol^-1, compared to 19.60 kcalmol^-1 for the intermediate. The resulting negative OS value implies that the heat of hydrogenation for the bridgehead olefin is lower than normal, even compared to medium size ring cycloalkenes. As the OS energy is negative, the alkene intermediate can be considered as hyperstable.

Therefore the reaction of these alkenes will be very slow due to its stability compared to its hydrogenated product.

Modelling Using Semi-Empirical Molecular Orbital Theory

Introduction

From the exercises carried out in the previous sections, it was demonstrated that the use of a molecular modelling method (e.g. MM2) has its limits as it is based on classical mechanics. This can be seen in the example concerning the Diels-Alder reaction, where the major endo product was wrongly predicted to be the minor product by the MM2 program, as the secondary orbital interactions were not taken into consideration. Therefore, other methods were developed to consider the electronic effects that contribute to the total energy of a molecule.

The development of semi-empirical methods allowed for the consideration of the electronic effects, and the Hartree-Fock approximation is used here, based on the STO-3G (Slater- Type Orbitals) set. The STO-3G basis set is a linear combination of primitive Gaussian functions that contain equations that as a whole describes the wavefunctions of a molecule - akin to the Linear Combination of Atomic Orbitals (LCAO). In order to reduce the length of time required for calculations, only a minimal basis set is utilised in the calculation, and even electron repulsion energy terms are not included. As a result, the values obtained from this method has a higher degree of inaccuracy, and these are accounted for by including experimentally-derived parameters. A consequence of including these parameters, the accuracy of the results depends on the molecule that is being studied and the molecule that has been modelled - from which the parameters are derived.

The Hartree Fock (HF) method also comes with its limits, one of which is due to the fact that the HF method calculates the average effect of electron repulsion, but does not consider the interaction of individual electrons with each other. This means that electrons are forced very close to each other or electrons placed far apart have the same probability as long as their distances from the core nucleus is the same. Therefore the main limit of the HF method is that the energies calculated by the program is always higher than the real energy of the molecule. Also, the approximations utilised in this method are the Born-Oppenheimer approximation, omission of core electrons, central field approximation and the omission of relativistic effects lead to the inaccuracies observed in the models calculated by the method. Fortunately, the inaccuracies induced by these approximations are reliably small for organic molecules, and the values obtained can be relatively accurate.

Alternatively, other methods using calculations from first principles, which take into account most, or all energy terms. These calculations however will require long computational times, and some of these known methods are Post-Hartree-Fock such as a quadratic configuration interaction, which corrects for the size consistency errors that arises from the calculation method.

Regioselective Addition of Dichlorocarbene

The regiospecific addition of dichlorocarbene to unsaturated C=C bond of napthalene occurs on the double bond endo to the chlorine atom on the bridgehead carbon. With the starting naphthalene being asymmetric, as seen in the reaction scheme below, where the chlorine atom is pointing in a particular direction with the hydrogen atom pointing in the opposite direction, the addition reaction that occurs is also regioselective. However, the selective addition onto the alkene endo to the chlorine at first seems to necessitate an undergoing of steric repulsion to give the final product, but the calculations that follow explain why this addition is favoured.

A minimisation carried out on the molecule in focus will give the following set of energy values. The apparent distance disparity between the hydrogen atom on the bridgehead carbon and the exo C=C double bond compared to the chlorine atom on the bridgehead carbon and the endo C=C bond (2.791Å and 3.178Å), and this observation could at this point be attributed to an effort to reduce the steric clash brought on by the large chlorine atom. The MM2 program does have the computing ability to reveal why this effect has been observed.

Table 11: Energy of the Naphthalene Compound

Energy Contribution	Energy /kcalmol-1
3D Image
Stretch	0.6168
Bend	4.7944
Stretch-Bend	0.0413
Torsion	7.6318
Non-1,4 VDW	-1.0769
1,4 VDW	5.781
Dipole/Dipole	0.1118
Total Energy	17.9000
JMol

Following the results from the MM2 optimisation, a MOPAC-PM6 optimisation was carried out to give a total energy of 40993kcalmol^-1. This value is very different from the total energies obtained from the MM2 method because both methods do compute energies in a different manner, leading to energy values that cannot be compared. Shown in the following diagrams are the molecular orbitals of the naphthalene compound.

The HOMO-2, HOMO-1, HOMO, LUMO, LUMO+1, LUMO+2 MOs

HOMO-2	HOMO-1	HOMO
LUMO	LUMO+1	LUMO+2

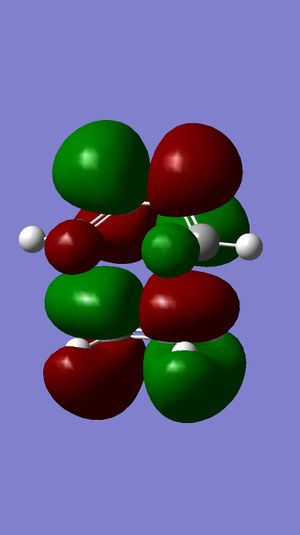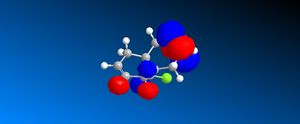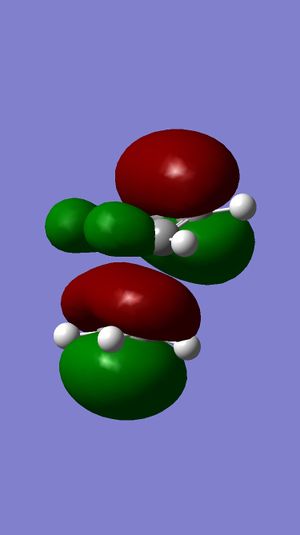
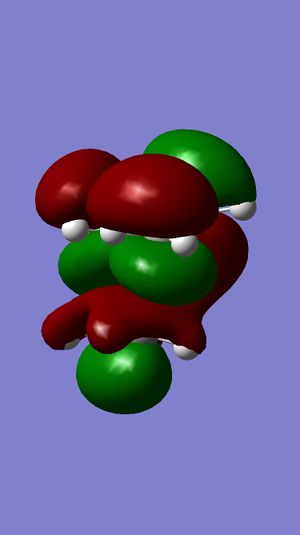
The minimising of the energy and optimising of the geometry with the use of the HF method led to the realisation of the above molecular orbitals. It can be observed from the above pictures that the HOMO of the C=C endo to the C-Cl bond has a larger electron density compared to the HOMO of the C=C exo to the C-Cl bond. This larger electron density contributes largely to its higher nucleophilicity as compared to the exo C=C bond, through the ease of attack and interaction between the molecular orbtaisl, thereby increasing its reactivity towards electrophiles. Another factor which increases the reactivity of the endo alkene and increases the stability of the exo alkene is the interaction of the exo C=C π orbitals with the C-Cl σ* orbitals in the HOMO-1 orbital, leading to an enhanced stability and a lower susceptibility to electrophilic attack. The combination of these two factors lead to the selective reactivity of the endo-alkene.

Compared to literature, the HOMO generated from the MOPAC-PM6 method is similar to that seen in literature. However the comparison of the other molecular orbitals with literature leads to a reasonable level of discrepancy which is due to the use of the PM3 method for the MOPAC calculation as compared to the PM6 method used in these calculations for this report.

Influence of the C-Cl bond on the Vibrational Frequencies of Molecule 12

In this section, the stretching frequencies of the exo and endo C=C bonds, including the C-Cl bond itself will be examined. It is theorised that the C-Cl bond present will have an effect on the stretching frequencies of the C=C bonds present in the molecules 12 and 13 as shown in the diagram below. Molecule 13 is the result of hydrogenating the anti alkene.

Diagram of the molecule 12 and partially hydrogenated product 13

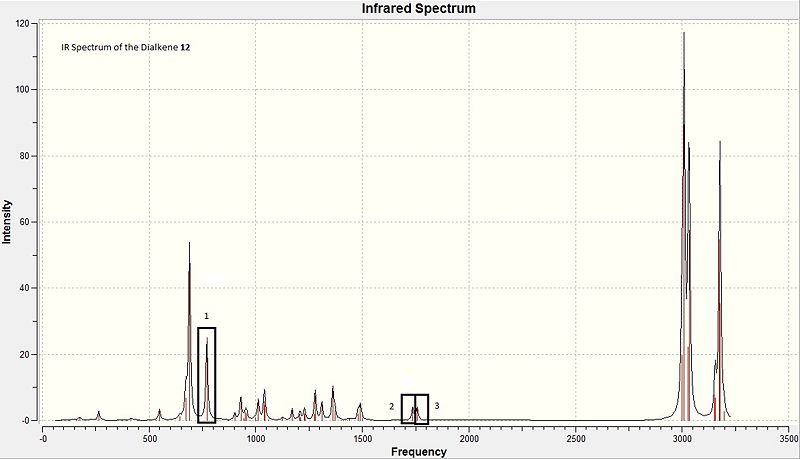
The IR spectra for the molecule 12 and 13 can be found at DOI:10042/to-7352 and DOI:10042/to-7351 respectively. The following table contains the data containing the DFT-generated IR stretches.

Table 12: Selected IR values of molecules 12 and 13

Molecule	Box	Bond	Stretching Frequency /cm-1
12	1	C-Cl	770.802
12	2	exo C=C	1736.97
12	3	endo C=C	1757.43
13	4	C-Cl	779.922
13	5	endo C=C	1753.76

First, the IR of the dialkene is shown in the diagram below with the key stretches highlighted in boxes. The most dominant C-Cl stretching observed through the animation provided on Gaussview03 involving the largest lengthening and contraction of the C-Cl bond is observed at a frequency of 770.80cm^-1. This value is reliably good when compared to literature. The two C=C stretches observed for molecule 12, 1737cm^-1 for the anti alkene and 1757cm^-1 for the syn alkene are different due to their chemically dissimilar environments, affecting the magnitude of the C=C bond stretching. In comparison to the literature values of C=C bond stretching frequencies with a value of 1670-1680cm^-1, the values obtained computationally are closer to the stretching frequency of the C=O functional group at 1670-1870cm^-1. This disparity in stretching frequencies could be due to the presence of the C-Cl bond in the vicinity of the C=C bond, where the possible C-Cl σ* interaction with C=C exo π orbital interaction could have lowered the energy of the exo C=C π orbital. This stabilisation increases the strength of the bond, resulting in a higher stretching frequency. For the endo alkene, the overall energy of the molecule may be lowered due to a possible orbital mixing with other anti-bonding orbitals which results in overall stabilisation, also resulting in a higher stretching frequency as compared to literature.

IR of the Dialkene

For the monoalkene, the IR spectrum shown in the diagram below shows the key stretches highlights in boxes also. The corresponding values for stretches can be viewed in table 12. Here, the existence of the C-Cl bond at 780cm^-1 corresponds well to literature values as quoted above. The existence of a single strong stretch for the endo alkene is in line with the presence of only 1 alkene in the monoalkene 13. The frequency for the endo alkene in 13, 1754cm^-1 compared to that of 12's frequency at 1757cm^-1 are highly similar, and the discrepancy with literature values as explained for molecule 12 applies to molecule 13 also.

IR of the Monoalkene

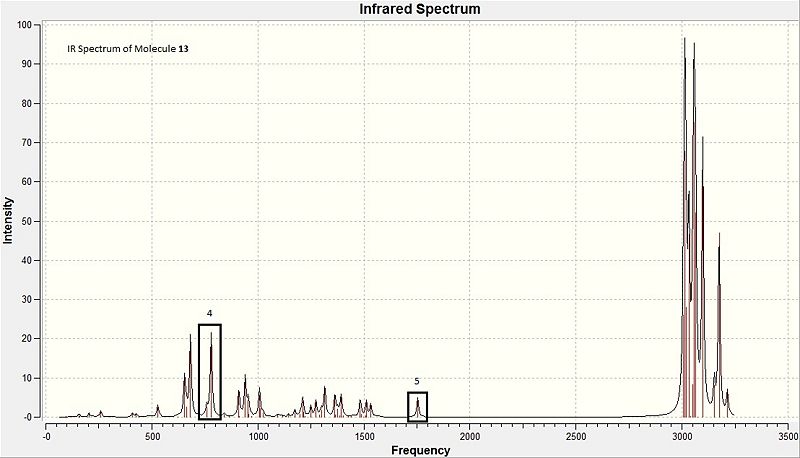
One general discrepancy with literature is that the apparent relative weakness of the anti alkene compared to the syn alkene implies that the anti C=C would be easier to break, and hence more reactive. This directly contradicts journal findings where it was discovered that the syn alkene preferentially reacts with dichlorocarbene. This can be rationalised by the fact that the calculated vibrational frequencies here consider the energies of both the σ and π orbitals, which results in the findings as aforementioned. However, in the reaction of the alkene with dichlorocarbene, the reactivity of the π bond is in focus - and not the σ bond, and hence this method is not specific enough to the reaction in study. Possible alternatives would be molecular orbital theory, as the energy of the participating MO is involved, and for this case the HOMO participates in this reaction, for which the electron density for the syn alkene is large, thus predicting correctly the selectivity of the reaction.

Structure-Based Mini Project Using DFT-Based Molecular Orbital Methods

Introduction to chosen reaction

In this section of the report, a mini project will be carried out where a specific asymmetric reaction is chosen, and its isomers examined through various modelling methods. The modelling methods engaged in the previous sections (MM2, DFT, etc.) will ideally rationalise why a different reaction occurs in different conditions, and will validate the reliability of the results from a journal. In the reaction chosen, the regioselective reaction of 1,3,7-Trihydroxyxanthone with 3-methyl-2-butanal - commonly known as prenal - under different conditions to give the isomers Osajaxanthone (compound 14) and Nigrolineaxanthone F (compound 15). The compounds and the conditions of the reactions are shown below:

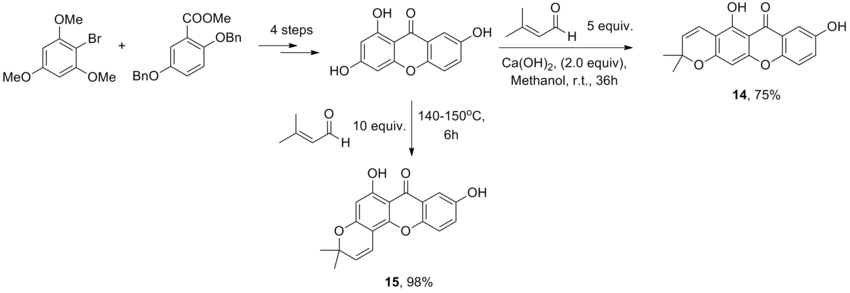
The synthesis of the natural product 15 has traditionally resulted in the formation of both compounds 14 and 15. These two compounds are difficult to separate. Therefore, it is important that compound 15 can be selectively synthesised, and this has been successfully done under thermodynamic control, whereas the synthesis of product 14 has been isolated in a major fraction under kinetic control.

Prenal and 1,3,7-Trihydroxyxanthone were condensed together to give a corresponding benzopyran-like intermediate through an aldol-type condensation, followed by a 6π electron cyclisation. The coupling reaction between the two starting molecules can theoretically occur at the 2, 4, 6 and 8 positions, but the thermodynamic stability upon attack of these positions are reported as 4 > 2 > 8 > 6. In particular, the 2 and 4 positions will be in focus here due to their reactivity to give the products 14 and 15 as the ring containing two hydroxy-functional groups has been doubly activated. As a carbanion will be generated in the course of the reaction, the attack at position 4 gives a more stable thermodynamic product due to the presence of the carbonyl and α,β unsaturated carbonyl (generated when converted from enol to keto form). In the same manner, the presence of the 1,3 dicarbonyl system (generated in the same way as before) will stabilise the carbanion generated. The mechanisms for the reactions are shown in the figures below.

Image showing the numbering of the carbon atoms

Mechanism for the formation of both compounds 14 and 15

Conformational Analysis of the Isomers 14 and 15

Table 13: MM2 energies of products 14 and 15

Type of Energy /kcalmol-1	Osajaxanthone 14	Nigrolineaxanthone F 15
Stretch	1.8316	1.7391
Bend	7.2904	7.4126
Stretch-Bend	0.0708	0.0705
Torsion	-7.9691	-8.0662
Non-1,4 VDW	-6.5883	-6.9258
1,4 VDW	21.5295	21.5897
Dipole/Dipole	0.069	0.173
Total Energy	16.234	15.993

Table 13 shows the relative energies of the different isomers, and it can be observed that the relative energies do not exactly show a great difference, weakly justifying the claim that the product 15 is a thermodynamic product.

Further energy minimisation of the products gave the following isomers in the conformations seen below:

Table 14: Diagrams of DFT Minimised molecules

Type	Product 14	Product 15
JMol
JPEG

From the diagrams of the optimised molecules seen about, it is observed that the molecules are rigid and do not have a large number of possibilities for conformations. The main xanthone skeleton is planar and it is observed that the newly formed ring has a slight degree of bending, meaning that the bonds directly attached to the aryl ring are not completely planar.

¹³C NMR Analysis

In this section, the values for the ¹³C NMR run experimentally will be compared to that found in literature. The diagram below will facilitate the assignment of peaks to the correct carbon atoms.

Labelling of the carbon atoms for assignment

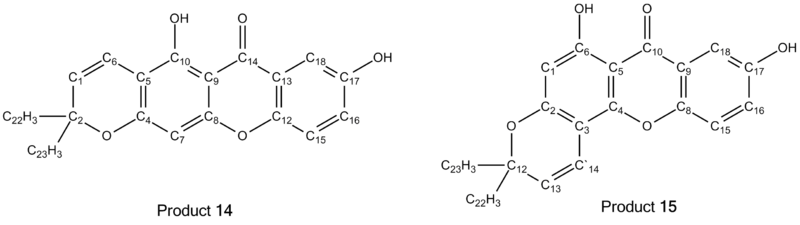
Product 14 Analysis

Calculated ¹³C NMR of Product 14

Table Comparing Literature and Calculated Values; *The carbon atoms are assigned according to the numbering shown in the previous section.

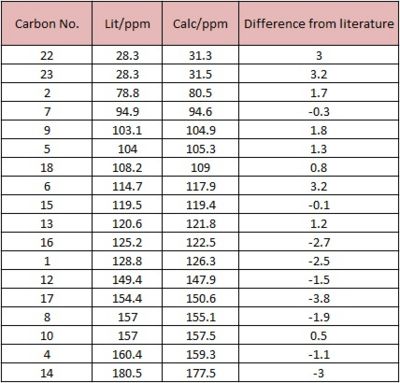
From the table above, all the carbon atoms have been accounted for in both the calculated and literature values. On examination of the magnitude of the difference in NMR values, it can be seen that there is a standard deviation from the literature values, all of which are not more than +/-5ppm. Due to the inherent error that can be found in these calculations, the error of +/-5ppm is a reasonable range to conclude that the calculations done by the DFT method are reliable. As a result, the structure that has been optimised by the Gaussian method is close to the actual structure of the molecule - that can be seen in literature.

Product 15 Analysis

Calculated ¹³C NMR of product 15

Table Comparing Literature and Calculated Values; *The carbon atoms are assigned according to the numbering shown in the previous section.

From the table above, all the carbon atoms have again been accounted for, and the magnitude of the differences between the values obtained from literature and calculations are reasonably small. It can therefore be concluded again that the calculations done by the DFT method are reliable, and the structure that has been optimised by the Gaussian method is close to the actual structure of the molecule seen in literature.

Overall Analysis

For both compounds, the correct products and accurate conformations have been calculated by the program. Minimal deviations from the literature values could be due to the fact that a real NMR run at specific temperatures will take into account all the conformations that the molecule can be found in, in contrast to this method, which only considers the most probabfind le conformation of the molecule. In this case, as the data fits well with each other, it can be said that the most probable conformers have been attained through the optimisation methods. Additionally, the influence of the solvent used in the NMR run has not been considered by the method, as the solvent might have a real effect on the conformation of the molecule. As a result, deviations can be expected in the calculations obtained.

Closer examination of the data reveals that the peak with the largest difference is the carbon on the 7-position of the xanthone backbone. This could be due to the inherent error due to Spin-Orbit coupling errors. With the appropriate corrections, the deviation from literature values will not be very noticeable. Overall, the difference in resonance signals of both isomers are not very large, and hence identifying these isomers through ¹³C NMR may not be the most effective way of identifying each isomer. One of the effective ways of identifying the isomers would be obtaining the melting points of the solid, or through x-ray crystallography.

The NMR calculations for product 14 can be found at DOI:10042/to-7426 and for product 15, DOI:10042/to-7427 .

IR Analysis

In an effort to find ways to distinguish both molecules, an IR calculation was also done for both molecules, and the information and comparison to literature can be seen in the tables below. Additionally, the IR calculations can be viewed at the following links: product 14 DOI:10042/to-7430 , and product 15 DOI:10042/to-7431 .

Analysis for Product 14

Calculated IR of Product 14

Table of assigned IR peaks from the calculated values

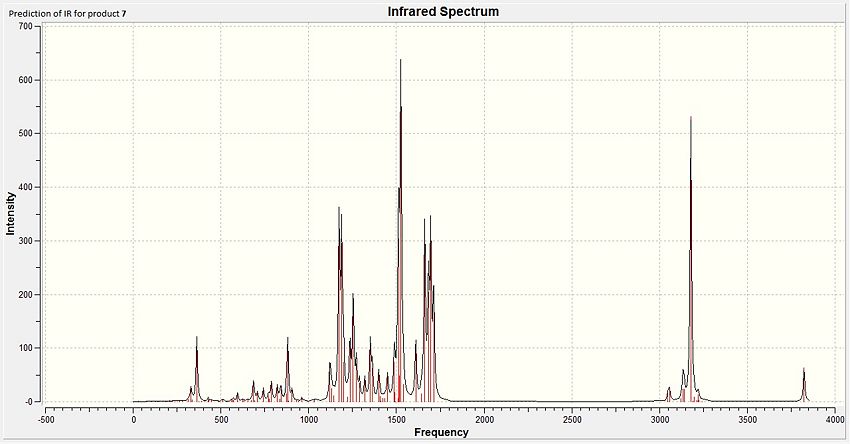
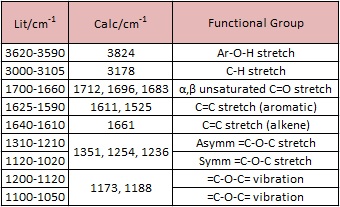
From the table and diagram above, it can be observed that some of the predicted IR values have been slightly overestimated by the DFT modelling method. Fortunately, all of the key functional group peaks have been observed although their errors have to be considered. It is suggested that an empirical correction by reducing the stretches by 6% could give appropriate values for the stretches as the DFT method employed normally overestimates the stretches of the IR vibrations.

In particular, the peaks for the phenol groups (3824cm^-1), carbonyls (1712, 1696, 1683 cm^-1) and phenyl rings (1611, 1525cm^-1) are the most intense and can be observed via a cursory comparison of the table shown with the IR spectrum presented above.

Analysis for Product 15

Calculated IR of Product 15

Table of assigned IR peaks from the calculated values

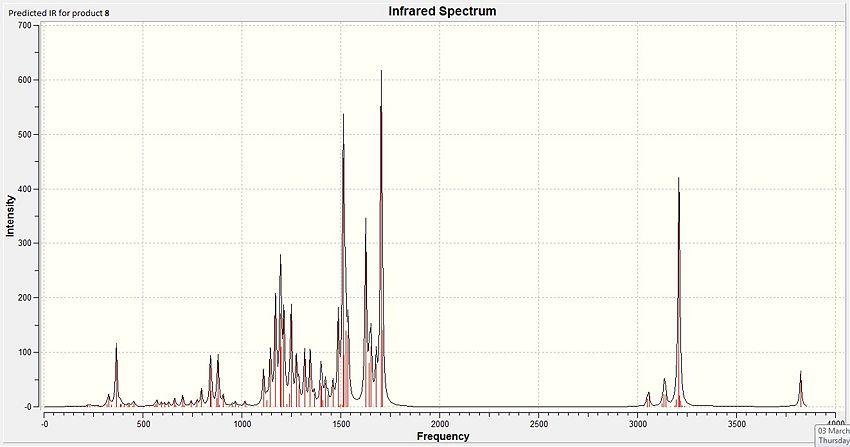
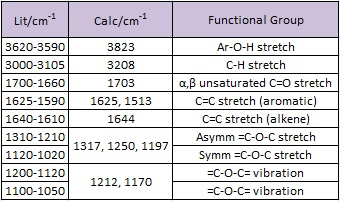
Likewise for product 15, some of the IR values have been overestimated by the DFT method and could use an empirical correction for a better estimation of the true IR values. Also, the peaks that are expected in the IR are all seen in this predicted IR spectrum. Particular to this molecule, the peaks for the phenol group (3823cm^-1), carbonyls (1703 cm^-1), and phenyl rings (1625, 1513 cm^-1) are the most intense and can be observed in the spectrum shown above.

Overall Analysis

From the two tables and diagrams above, the IR spectra calculated by the DFT modelling method seem to give peaks that are highly similar for both molecules. Although the environment of the conjugated alkenes in both products could be different due to their varying positions, which could affect the strength of the C=C bond and hence it will be reflected in the stretching frequency seen in the spectra, this difference may prove to be very small and will not differentiate both isomers easily. Hence the use of IR spectroscopy to identify each particular isomer is not a particularly good method, and other most effective methods could be ¹H NMR. The resonance signals of the hydrogen atoms will most likely be different due to the positions of the functional groups on the compounds 14 and 15. This will result in chemical shifts that have a slightly larger difference as compared to the two spectroscopy methods carried out here.

However, the analysis for ¹H NMR was not carried out to due to the larger errors inherent in the DFT modelling calculations, which would be counterproductive if extensive error analysis has to be done for a method that was meant to facilitate the discovery of the most stable conformer for each isomer.

Conclusion

Molecular modelling has been successfully used to predict the most stable conformation of the isomers, ¹³C NMR and IR spectra of the molecules under study. While these results correspond well to that of literature, there deviations from the literature values could be due to the fault of the modelling method used to optimise the conformation of the molecule, and on top of that, inherent errors found in the use of the DFT modelling method used to calculate the values for the spectra used here.

Through the analysis carried out in the previous sections, it can be concluded that the DFT modelling method has shown its ability to predict spectroscopy values to a reasonably accurate degree when compared to literature values. The results recorded correspond well to that of literature and proves that the literature values are valid. Through this exercise, the power of computational chemistry can be seen in its ability to valid researh results, and also allow for the prediction of conformational products in an asymmetric reaction.