User:Molecular Modelling (jr1416)
BH3 section
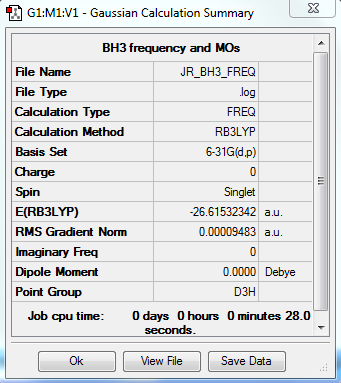
The RB3LYP method and a basis set of 6-31G(d,p) was used to calculate and optimize the structure of BH3.
Summary Table
.PNG)
Item Table
Item Value Threshold Converged? Maximum Force 0.000190 0.000450 YES RMS Force 0.000095 0.000300 YES Maximum Displacement 0.000747 0.001800 YES RMS Displacement 0.000374 0.001200 YES
Frequency Analysis
Frequency analysis log file JR_BH3_FREQ.LOG
Low frequencies --- -0.2260 -0.1035 -0.0054 48.0278 49.0875 49.0880 Low frequencies --- 1163.7224 1213.6715 1213.6741
Animation
optimised borane molecule |
Infrared Vibrational Analysis
| Mode | Frequency (cm-1) | Intensity | Symmetry | IR activity | Type of vibration |
|---|---|---|---|---|---|
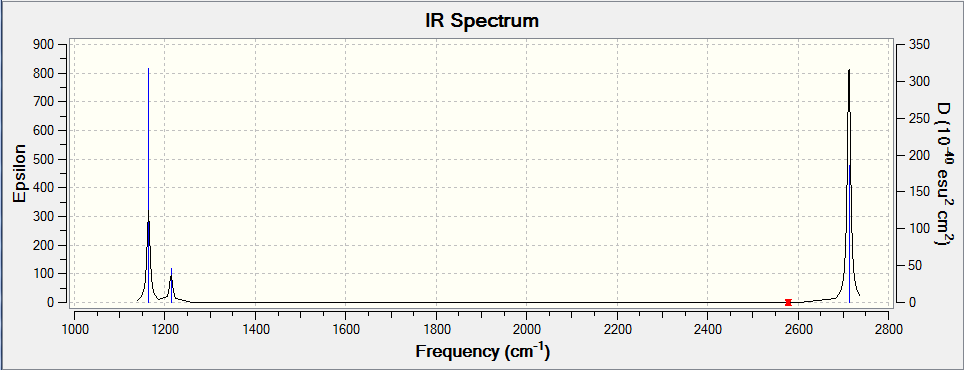
| 1 | 1160 | 92 | A2" | Active | Out of plane bend |
| 2 | 1210 | 14 | E' | Active | Bend |
| 3 | 1210 | 14 | E' | Active | Bend |
| 4 | 2580 | 0 | A1' | Inactive | Symmetric Stretch |
| 5 | 2710 | 126 | E' | Active | Asymmetric stretch |
| 6 | 2710 | 126 | E' | Active | Asymmetric stretch |
IR Spectrum
.PNG)
The number of peaks corresponds to the number of non-degenerate IR active peaks, this is why only 3 peaks are seen in the computed spectrum. Only these modes provide a change in dipole moment of the molecule, a requirement for absorption of a photon.
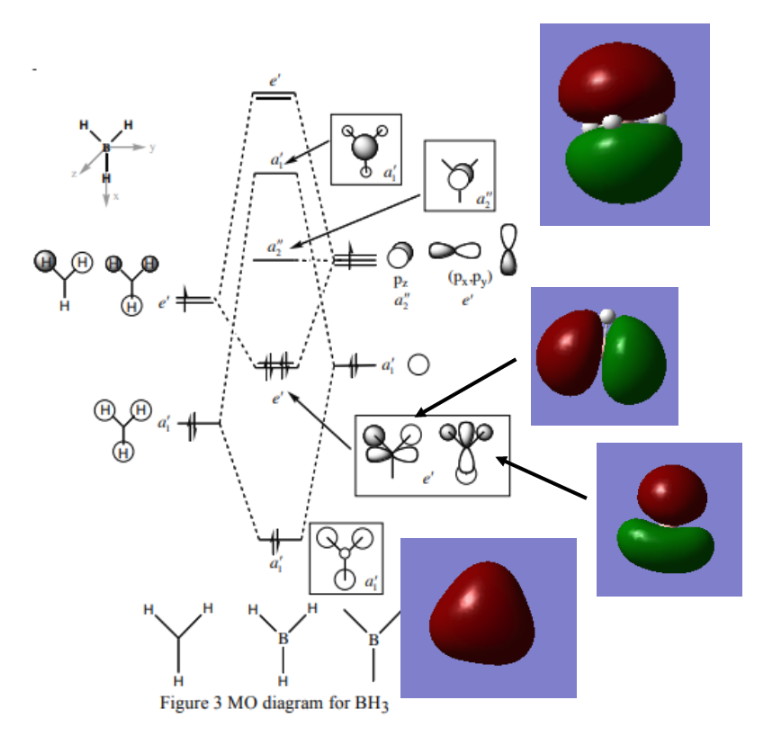
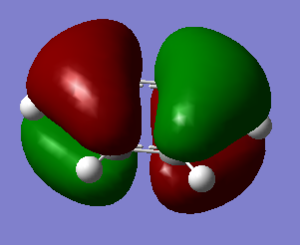
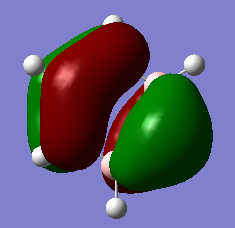
Molecular Orbitals
.PNG)
Taken from http://www.huntresearchgroup.org.uk/teaching/teaching_comp_lab_year2a/Tut_MO_diagram_BH3.pdf
The real MO's are more diffuse than the LCAO's and also have the constructive and destructive phase overlaps as well. The qualitative MO's are a good estimate of the real MO's and can be calculated much more easily and thus are very useful in analysis.
Smf115 (talk) 17:00, 23 May 2018 (BST)Nice inclusion of the MOs in the diagram however, the top two are missing. You correctly mention the similarity and the differences, an improvement though would be to highlight the more subtle differences in shape more explicitly such as by looking at 2a1' as an example.
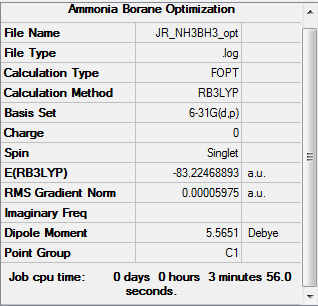
Ammonia Borane
NH3 Optimization
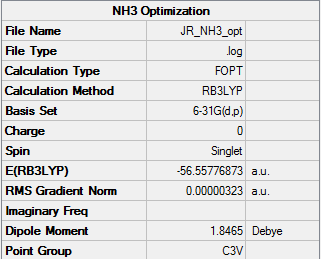
The RB3LYP method and a basis set of 6-31G(d,p) was used to calculate and optimize the structure of NH3.
Item Table
Item Value Threshold Converged? Maximum Force 0.000006 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000012 0.001800 YES RMS Displacement 0.000008 0.001200 YES
Log File
Summary Table
.PNG)
Frequency Analysis
Low frequencies --- -8.5646 -8.5588 -0.0044 0.0454 0.1784 26.4183 Low frequencies --- 1089.7603 1694.1865 1694.1865
Animation
optimised ammonia molecule |
Energy
E(NH3) = -56.5578 a.u. (-148490 kJmol-1)
NH3BH3
The RB3LYP method and a basis set of 6-31G(d,p) was used to calculate and optimize the structure of NH3BH3.
Item Table
Item Value Threshold Converged? Maximum Force 0.000122 0.000450 YES RMS Force 0.000058 0.000300 YES Maximum Displacement 0.000513 0.001800 YES RMS Displacement 0.000296 0.001200 YES
Log File
Summary Table
.PNG)
Frequency Analysis
Low frequencies --- -0.0013 -0.0011 -0.0011 14.4660 22.7381 41.6444 Low frequencies --- 266.6526 632.2253 639.1944
Animation
optimised borane molecule |
Energy
E(NH3BH3) = -83.2247 a.u. (-218510 kJmol-1)
NH3BH3 Energy of Reaction
Calculation
E(NH3) = -56.5578 a.u. (-148490 kJmol-1) E(BH3) = -26.6153 a.u. (-69880 kJmol-1) E(NH3BH3) = -83.2247 a.u. (-218510 kJmol-1)
Er = E(NH3BH3)-(E(NH3)+E(BH3)) = -140 kJmol-1
Interpretation
This value for the association energy for ammonia borane is a sensible value as the energy of a C-N covalent bond is around -305 kJmol-1[1]. The bond energy of this dative bond is less due to the poorer overlap between B and N orbitals as compared to C and N. Compared to the C-N bond, the B-N bond is weak due to the poorer overlap integral.
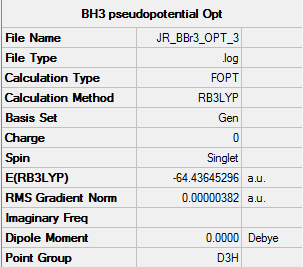
BBr3
The B3LYP method and a basis set of 6-31G(d,p), for the Boron atom, and LANL2DZ, for the Bromine atoms, was used to calculate and optimise the structure of BBr3.
Item Table
Item Value Threshold Converged? Maximum Force 0.000008 0.000450 YES RMS Force 0.000005 0.000300 YES Maximum Displacement 0.000036 0.001800 YES RMS Displacement 0.000023 0.001200 YES
Log File
Summary Table
Frequency Analysis
Low frequencies --- -0.0137 -0.0064 -0.0046 2.4315 2.4315 4.8421 Low frequencies --- 155.9631 155.9651 267.7052
Animation
optimised bromoborane molecule |
DSpace link
Smf115 (talk) 16:56, 23 May 2018 (BST)Great structure information throughout with the calculation methods clearly detailed for each structure, including the pseudopotential used for BBr3.
Project section - Investigating Aromaticity
Benzene
The Method used for the optimisation of Benzene is RB3LYP and the basis set used is 6-31G(d,p).
Item Table
Item Value Threshold Converged? Maximum Force 0.000194 0.000450 YES RMS Force 0.000077 0.000300 YES Maximum Displacement 0.000824 0.001800 YES RMS Displacement 0.000289 0.001200 YES
Summary Table
.PNG)
Log File
Frequency Analysis
Low frequencies --- -16.9682 -14.6636 -14.6636 -0.0055 -0.0055 -0.0005 Low frequencies --- 414.1239 414.1239 620.9400
Animation
optimised borane molecule |
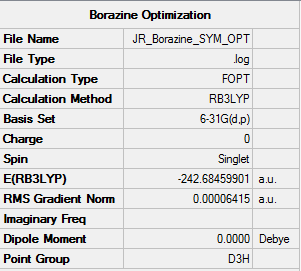
Borazine
The Method used for the optimisation of Borazine is RB3LYP and the basis set used is 6-31G(d,p).
Item Table
Item Value Threshold Converged? Maximum Force 0.000085 0.000450 YES RMS Force 0.000033 0.000300 YES Maximum Displacement 0.000252 0.001800 YES RMS Displacement 0.000075 0.001200 YES
Summary Table
.PNG)
Log File
Frequency Analysis
Low frequencies --- -0.0013 -0.0012 -0.0012 3.4753 4.3539 6.8594 Low frequencies --- 289.7049 289.7804 404.4236
Animation
optimised borane molecule |
Charge Analysis
Animation Table
| Benzene Charge Analysis | Borazine Charge Analysis | |
|---|---|---|
| Colour Analysis | 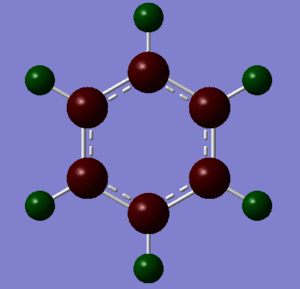.PNG)
|
.PNG)
|
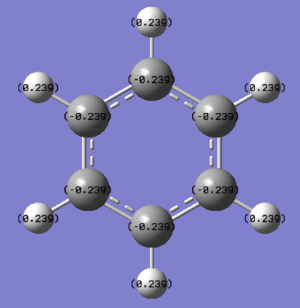
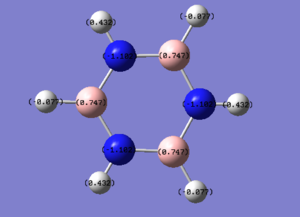
| Numerical Analysis | .PNG)
|
.PNG)
|
Charge Table
| Hydrogen | Carbon | Nitrogen | Boron | |
|---|---|---|---|---|
| Benzene | 0.239 | -0.239 | ||
| Borazine | 0.432 / -0.077 | -1.102 | 0.747 |
Discussion
The benzene charge distribution shows a symmetrical arrangement of the charge with the more electronegative carbon, Mulliken electronegativity 2.55, having a charge of -0.239 and the more electropositive hydrogen, Mulliken electronegativity 2.2, having a charge of 0.239. Compared with borazine, there is a relatively low charge distribution in benzene due to the lower polarity between carbon and hydrogen. Each carbon and each hydrogen has the same partial charge, creating a negatively inner ring which is susceptible to electrophilic attack.
The borazine NBO analysis shows that there is a high distribution of charge with the highly electronegative nitrogen, Mulliken electronegativity 3.04, compared with the electropositive boron, Mulliken electronegative 2.04, giving a polar bond which results in borazine having an alternating charge distribution (N=-1.102, B= 0.747) in the inner ring. This makes the ring susceptible to electrophilic attack at the nitrogen and nucleophilic attack at the boron on the ring. Due to the differing electronegativities of the inner ring substituent atoms, two hydrogen charge environments are produced. Hydrogen has a Mulliken electronegativity of 2.2 [2]and therefore is more electronegative than boron, giving each hydrogen bonded to a boron a charge of -0.077, whilst nitrogen is more electronegative than hydrogen resulting in nitrogen bound hydrogens a charge of 0.432.
| Structure | Inner ring charge | Reactivity of ring | Hydrogen environments |
|---|---|---|---|
| Benzene | Negative | Electrophilic attack on C | 1 |
| Borazine | Positive on B, Negative on N | Nucleophilic attack on B, Electrophilic attack on N | 2 |
Analysis
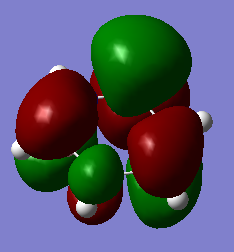
Molecular Orbital Analysis
| MO description | Benzene MO | Borazine MO | Comments |
|---|---|---|---|
| In phase s-orbital Bonding MOs | .PNG)
|
.PNG)
|
These are MOs 7 for both benzene and borazine, they are both completely in phase sigma bonding molecular orbitals. Benzene shows an MO comprised of the 1s hydrogen orbitals and 2s carbon orbitals overlapping in phase to
produce a bonding orbital, whilst in the analogous borazine MO, there is only overlap between the 2s of the nitrogen atomic orbitals and the 1s of the hydrogens attached to these. This results in the raising in energy of the | | borazine MO, as there is less delocalisation due to the poor energy match between the 2s boron and nitrogen atomic orbitals leaving the 2s of the boron and attached hydrogens out of the MO. π bonding MOs with 1 node |
| π bonding MOs with 1 node | .PNG)
|
.PNG)
|
These are MOs 20 for both benzene and borazine, they are both π bonding orbitals with 1 node across the centre of the molecule. The high symmetry of the benzene molecule, with all carbons having equal energy 2p orbitals,
means that there are equal sized molecular orbitals with 1 nodal plane, whilst the borazine MO shows a 2 different sized MOs due to the lower symmetry of the molecule and the energy differences of the 2p orbitals. The larger of the 2 in phase π clouds in the borazine molecule is attributed to the N-B-N 2p overlap, due to nitrogens 2p orbitals being lower in energy and thus contributing more to the bonding MO, the smaller is attributed to the B-N-B 2p overlap. |
| π anti-bonding MOs with 2 nodes | .PNG)
|
.PNG)
|
These are MOs 23 for both benzene and borazine, they are both π anti-bonding orbitals with 2 nodal planes at right angles to one another creating 2 in phase 2p-2p orbital overlap MO clouds and 2 out of phase 2p MO clouds. The
benzene molecule due to its equal energy of all the C 2p orbitals maintains 2 same sized out of phase p-orbitals and 2 in phase 2p-2p orbital MO clouds. Whilst the borazine contains N which give larger orbitals due to lower energy 2p orbitals, the larger out of phase p-orbital is due to a nitrogen 2p orbital, the smaller due to boron, both the overlapping in phase 2p-2p MO clouds are due to B-N 2p overlap and thus have the same contribution to the MO. |
Smf115 (talk) 16:46, 23 May 2018 (BST)Good range of charcter shown by the chosen MOs which are described by the correct terminology. Nice justification of differences due to electronegativity and mention of the contributing AOs. To improve, consider other comparison points such as symmetry and notice that there are actually 2 nodal planes for MO 20 in both molecules and 3 nodal planes for both MO 23's.
Discussion on Aromaticity
Aromaticity was first identified by Kekule with respect to the molecule of benzene, his model suggested interchanging double bonds around the ring, which changed so rapidly that an average delocalised pseudo-structure is observed. This theory has since been updated many times, to the quantitative rules that we know as Huckels rules for aromaticity; 4n+2 p electrons, planar contiguous ring, orthogonal p orbitals to ring plane. These guidelines rely on the aromaticity of a compound being derived from combining in phase pz atomic orbitals from the linear combination of atomic orbitals theory (LCAO) which works for neutral homocyclics like benzene at room temperature but later we will see why this model falls apart for aromaticity as a whole.
With more powerful computational methods available to us now it has been discovered that benzene at 20 K adopts a boat conformation, whilst retaining its aromaticity[3]. This definitively breaks Huckels rule that the ring needs to be planar to be aromatic, suggesting that the aromaticity should be broken, however it isn't and therefore there must be other factors contributing to the aromaticity of the molecule. The reasoning behind this is thought to be due to the aromaticity actually having a contribution from s-orbitals as well as overlapping p-orbitals, which can be visualised by looking at the 7th molecular orbital of benzene above. This molecular orbital clearly shows the a delocalised MO produced from the overlap of all of the s-orbitals, a similar MO is also produced in borazine's analogous MO. This shows that the basic interpretation of overlapping pz orbitals is not enough to explain the complex factors involved with the aromaticity of a molecule, instead calculations of MOs is a better method for visualising and understanding aromaticity.
Smf115 (talk) 16:54, 23 May 2018 (BST)Great use of MO 7 as an example of sigma-aromaticity within the molecules just studied and discussion of Huckels rule as a key concept of aromaticity.
Smf115 (talk) 16:54, 23 May 2018 (BST)Overall a very good and well presented report with a few mistakes across the first section.
References
- ↑ B═N Bond Cleavage and BN Ring Expansion at the Surface of Boron Nitride Nanotubes by Iminoborane Rajashabala Sundaram, Steve Scheiner, Ajit K. Roy, and Tapas Kar The Journal of Physical Chemistry C 2015 119 (6), 3253-3259 DOI: 10.1021/jp512753n
- ↑ Revised Mulliken electronegativities: I. Calculation and conversion to Pauling units Steven G. Bratsch Journal of Chemical Education 1988 65 (1), 34 DOI: 10.1021/ed065p34
- ↑ Application of AIM Parameters at Ring Critical Points for Estimation ofp-Electron Delocalization in Six-Membered Aromatic andQuasi-Aromatic Rings, Dr. M. Palusiak, Prof. Dr. T. M. Krygowski, DOI: 10.1002/chem.200700250