Rep:One! how many time travelers does it take to screw in a lightbulb

The Cope Rearrangement

Optimizing the Reactants and Products

In order to investigate the appropriate aspects of this reaction, we much first create the molecule; as such, 1,5 hexadiene was constructed in it's anti form, using ChemBio 3D, and an initial minimisation was run (MM2). This basic minimisation took a matter of seconds and seemed to prevent the later calculations in GaussView from failing (although rare, this did happen to other students).

The MM2 minimised 1,5 hexadiene was copied into GaussView so taht a more complicated minimisation could be run. The molecule was then submitted for a Hartree Folk minimisation (3-21G basis set). The checkpoint file was named appropriatly, and the memory designated for use was set to 1000MB (this was kept for all future calculations, since the laptops on which these calculations were run had 2GB of RAM (and XP only takes about 500MB to run), 1000MB seemed like a safe amount to designate).

Once the calculation had completed, the energy of teh molecule was recorded and compared with the appendix values:

Energy of Anti 1,5 Hexadiene (Hartees)	-231.69253525
Point Group	Ci
Appendix Energy of anti2 1,5 Hexadiene (Hartees)	-231.69254

these energies are identical (to 8 s.f.) therefore it is almost certain that the constructed form of the anti 1,5 Hexadiene was that of anti2, and a quick look at the molecules confirmes this:

Constructed Anti 1,5 Hexadiene
anti2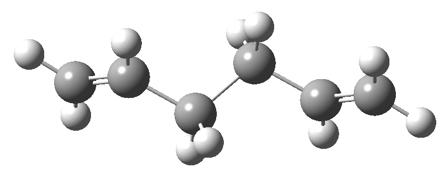

Next, this process was repeated with a gauche linkage, and the following data was compiled:

	Energy (Hartrees)	Point Group	Image
Constructed Gauche 1,5 Hexadiene	-231.68394354	C2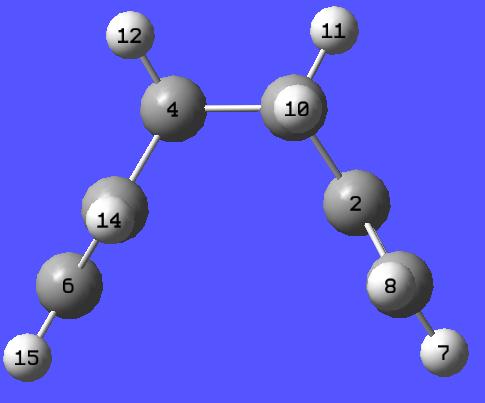
gauche2	-231.69167	C2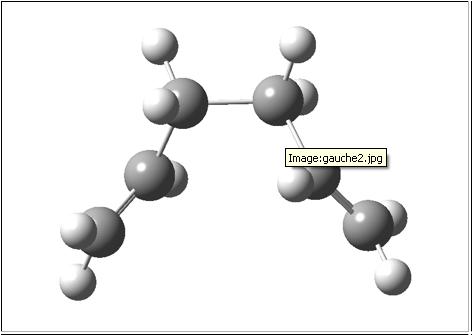

The conformer is therefore almost definatly the gauche2 version (even though the energies don't quite match up).

From initial analysis, it appears that the anti conformation is more stable, however it seems that an steric interactions have already been minimised in the initial estimate. As such, the data was compared to appendix 1. This showed that a gauche conformation was actually the most favoured.

It was therefore thougth prudent to replicate this data:

	Energy (Hartrees)	Point Group	Image
Constructed Lowest Energy Gauche 1,5 Hexadiene	-231.69266120	C2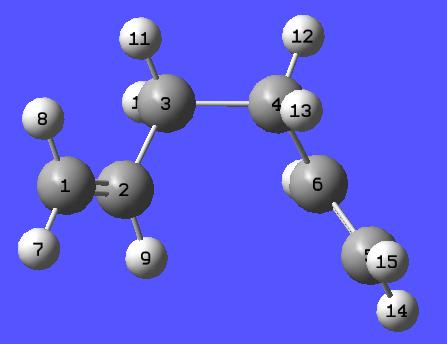
gauche3	-231.69266	C2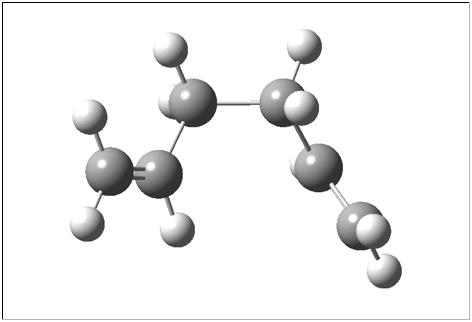

Again, the data all matches up. Therefore it can be deduced that i am fairly comfortable with the basic operations of GaussView

Since the C_i anti conformation of 1,5-hexadiene has already been HF/3-21G minimised, it was able to be immediatly scanned with a DFT/B3LYP method and 6-31G* basis set.

Once the calculation completed, the following data was compiled:

	HF/3-21G	B3LYP/6-31G*
Energy (Hartrees)	-231.69253525	-234.61171039
Geometry

(click on the appropriate "geometry" to enlarge)

As can be seen, the overall geometry of the molecule has only changed by a small amount: although that it is true that the C=C bond lengths change by almost 0.02 A, no other bond lenghts undergo such a large alteration, and all the bond angles remain roughly constant (change ≈ 1°). Therefore there has only been a minor affect to the molecular geometry, and similarly only a minor effect to the overall energy, however, the higher level calculatiosn does predict a more stable molecule.

Also, the point group has been maintained as _Ci.

Starting from the B3LYP/6-31G* optimised structure, a vibrational analysis of 1,5 hexadiene was able to be performed.

Once this calculation was complete, the vibrations of the moleucle could be reviewed. Although not recorded, there were no negative (imaginary) frequencies obtained, and data was recorded from the opened file:

	Calculated	Literature
Electronic energy	-234.61171039	-234.611710
Sum of electronic and zero-point Energies	-234.469204	-234.469203
Sum of electronic and thermal Energies	-234.461857	-234.461856
Sum of electronic and thermal Enthalpies	-234.460913	-
Sum of electronic and thermal Free Energies	-234.500776	-

(all energies in Hartrees)

As can be seen, all the values are very similar. In fact; they are all identical to 7 significant figures. Hence it is clear that the optimisations have run well and, as such, the correct geometries have been recorded.

Optimizing the "Chair" and "Boat" Transition Structures

The allyl fragment was constructed using GaussView, and was optimised with HF/3-21G level theory:

allyl fragment

This allyl fragment was then copied to a new window in GaussView twice, and these molecules were arranged into a rough guess of the actual transition state, with the inter carbon distances (between the carbons which we expect bonds to form) were set to 2.2 A:

Transition State Guess

This Transition State Guess was then optimized to a transition state (Berny), with the calculation of the Force Constant Once. the additional keyword "Opt=NoEigen" was added to the calculation, to prevent the calculation crashing if more than one transition state is calculated although this turned out not to be the case).

Upon completion, the file was reviewed and one imaginary vibtration was recorded (at -817.9 cm^-1):

jm906-817.9086_vibration

Here, we can clearly see this vibration, the molcular vibration takes one set of bonding carbons together, and then the other (even though one of the inter molecular C-C bonds seems to have formed on this representation).

This optimized TS guess, could then be further optimized using the frozen cordinate method. Another copy of the TS guess was opened in GaussView, and the redundant coordinate editor was used to freeze the C-C bonding carbons 2.2A from each other. This "frozen" set of molecules was then optimised under HF/3-21G level theory to a minimum.

The resulting geometry resembeled, very much, the former geometry, except that the bond inter molecule C-C distences were shorter.

This set of molecules was immediatly re-submitted into GaussView, but this time the Redundant Coord Editor was set to "Derivative" instead of "Freeze Coordinate". Again the optimization used HF/3-21G level theory.

This "Frozen Coordinate Method" molecule was then compared to the "HF/3-21G" optimized molecule:

	Intermolecular C-C Bonding distance	C-C-C allyl Bond Angle
HF/3-21G	2.019 A	120.5°
Frozen Coordinate Method	2.020 A	120.5°

As can be seen, there is not much of a change in the actual geometries of these two sets of molecules; this could be bacue the oridional set of molecules (before being optimized) was edited so that the intermolecular C-C bonding distances were approximatly equal to 2.02A (as suggested by the method).

Since this method has not performed a significantly better optimisation, we must now move onto a more complicated calculation; the QST2 method.

This works by taking prespecified reactants and products and interpolating the transition state between them.

However, this method requires a little more effor than the previous, fully automated, calculations:

A new GaussView window was opened so that a copy of the pre-optimized C_i molecule (anti2) could be created. Using the "Add to MolGroup" function, a window representing the "second step" of the molecule was created; into this, the molecule was copied a second time.

This copy was edited in the following way:

(click to enlarge)

so that the labeling of the atoms is consistant assuming that a C-C bond has formed between C₁ and C₆ and the C-C bond between C₄ and C₃ has broken.

This edited molecule was then set for an optimization and frequency analysis; optimizing to TS (QST2).

However, this calculaiton failed, and the folowing data was returned;

Failed QST2 calculation

As can be seen the molecule appears to have been "blown apart"; there are no longer any bonded hydrogens, which nowlie a large distance from the carbons, which have formed 2 allyl-like structures (one above the other), similar to the chair calculation transition state.

Therefore some further edditing is required;

(click to enlarge)

Here, the C₂-C₃-C₄-C₅ dihedral angles have been edited to 0°, and the C₂-C₃-C₄ and C₃-C₄-C₅ angles have been edited to 100°, in both the product and reactant.

This molecule was then optimised to TS (QST2), and had a frequency analysis run. However, the firs ttime this molecule was edited; the hydrogens were failed to moved, meaning that the the calculation errored. After consultation with Dr Bearpark, this was fixed, but there was still a problem, this time with the eigenvalues:

Inconsistency:  ModMin=   2 Eigenvalue= 9.64410716D-03

This error was overcome by allowing the force constant to be calulated once at the beginning of the optimization. This caused the molecule to follow the right path of optimization (before, the molecule had tried to optimize in the wrong way, and had managed to get suck between transition states).

With this ammendment, the calculation returned the correct transition state, which was analysed and this imaginary vibration (at -840.0 cm^-1) was recorded:

jm906Boat_transition_vibration

This Vibration showes one of the C-C bonds already formed, and only the vibration associated with this (seems to be a weakness of the JMol appelate used to upload this data), however, this vibration is repeated on both sides of the molecule and the inter molecular carbon bonds form and break between each of the terminal carbons.

Looking at the optimised structures;

Optimized Chair Transition Structure	Optimized Boat Transition Structure
jm906Chair_transition_state	jm906Boat_transition_state

It in not possible (at least form the above) to distinguish which conformer of the 1,5 hexadiene is present in either of the transition states (whether it's the C₁-C₂-C₃-C₄-C₅-C₆ or the C₃-C₂-C₁-C₆-C₅-C₄)

In order to solve this, we can use a method called Intrinsic Reaction Coordinate (IRC). This allows us to look at the reaction path from the transition structure to either product. It does this by taking small geometry steps in the direction of steepest gradient on the potential energy surface.

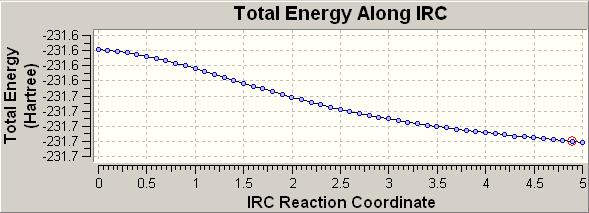
This calculation was run (on the boat conformer) with only initial force constance calculated, and 50 steps. However, the completed molecule had failed to minimise properly:

As can be seen, the minimal energy has not been reached, the gradient is still decreasing with number of iterations. What we are expecting in a fully minimised molecule is for the enrgy to start increasing again; showing that a minimum has been calculated.

Therefore the initial molecule was re-calculated, with the same IRC parameters, except now with force constants calculated every iteration to help the minimisation run better.

However, an error occured. For an unknown reason the link was abnormally terminated, and the calculation failed after 14 itterations. In the interests of time management, this calculation was not reatempted, and a different method of viewing the transition steps was used: the IRC-ed molecule was run with a normal optimisation, but the intermediate geometries were viewed:

IRC Data for Chair TS	Optimisation Date for Chair TS

(click to enlarge)

as can be seen, the minimisation in the IRC was quite gradule, and covered a large amount of ground, and the optimisation has finished this process off (note that it showes the starting energy for the IRC calculation (1) as well as the starting energy for the minimisation (iteration 2)). the minimisation gives an energy of -231.691667 a.u. for this transition state.

The intermediate geometries given in the optimisation adn the IRC allow us to see the "formation" of the bond and let us distinguish which bond is forming.

Now, the activation energies via the transition structures needs to be calculated. This was by taking the HF/3-21G optimised structures and re-optimising them, but this time with the, higher level, DFT/B3LYP method, with 6-31G* basis set.

Once these calculations returned, the following data was compiled:

Summary of Chair Transition State

	HF/3-21G	HF/3-21G	HF/3-21G	B3LYP/6-31G*	B3LYP/6-31G*	B3LYP/6-31G*
	Electronic energy	Sum of electronic and zero-point energies (0K)	Sum of electronic and thermal energies (298.15K)	Electronic energy	Sum of electronic and zero-point energies (0K)	Sum of electronic and thermal energies (298.15K)
Calculated Boat	-231.602802	-231.450929	-231.445300	-234.543080	-234.402302	-234.395967
Literature Boat	-231.602802	-231.450929	-231.445300	-234.543093	-234.402340	-234.396006

The calculated HF/3-21G energies are very similar to the given values, the geometry of the calculated transitin state is, therefore, very similar to the Literature HF/3-21G optimisation. The B3LYP/6-31G* energies are also very close. Hence the minimisations have followed the correct path and the geometry of the obtained transition state is very close to the actual transition state in nature.

Summary of Boat Transition State

	HF/3-21G	HF/3-21G	HF/3-21G	B3LYP/6-31G*	B3LYP/6-31G*	B3LYP/6-31G*
	Electronic energy	Sum of electronic and zero-point energies (0K)	Sum of electronic and thermal energies (298.15K)	Electronic energy	Sum of electronic and zero-point energies (0K)	Sum of electronic and thermal energies (298.15K)
Calculated Chair	-231.619322	-231.466700	-231.461340	-234.543080	-234.468283	-234.460967
Literature Chair	-231.619322	-231.466705	-231.461346	-234.556983	-234.414919	-234.408998

(all energies in hartrees)

Summary of Transition States

	Energy of Chair	Energy of Boat	Difference (Chair - Boat)
HF/3-21G	-231.619322	-231.602802	0.01652
B3LYP/6-31G*	-234.55308	-234.54308	0.01

(all energies in hartrees, unless otherwise stated)

Chair Activation Energies

	Energy of Chair	Energy of Anti2	Difference	Activation Energies(kcal/mol)	Literature Activation Energies(kcal/mol)
HF/3-21G	-231.619322	-231.6925353	0.07321325	45.94197329	45.70
B3LYP/6-31G*	-234.55308	-234.6117104	0.05863039	36.7910974	31.06

(all energies in hartrees, unless otherwise stated)

The calculated energy for the HF method is incredibly close to the energy found in literature, this is as expeced as all the conformer energies were vwery close to litererature values.

However, we see a substantial difference when we look at the DFT optimisation. The calculated activation energy is much higher than the literature value, and this would be the case if the DFT minimisation did not run to completion.

It is posssible for a calculation to complete without minimising the molecule fully, and that was probably the case here, at this higher level of theory. The next step, to fully minimising this molecule, would be to run the same calulation (DFT/B3LYP) but with a higher basis set (LanL2DZ). This would probably calculate a value for activiation energy much closer to literature.

boat Activation Energies

	Energy of Boat	Energy of Anti2	Difference	Activation Energies(kcal/mol)	Literature Activation Energies(kcal/mol)
HF/3-21G	-231.602802	-231.6925353	0.08973325	56.30842197	55.60
B3LYP/6-31G*	-234.54308	-234.6117104	0.06863039	43.0661874	41.96

(all energies in hartrees, unless otherwise stated)

Looking at the energies calulated in the case of the boat, they lie much closer to literature values; implying that, in this case, the optimisations were completed to a higher degree. As the difference is minimal, the calculated structures are a good approximation to these molecules in nature.

The Diels Alder Cycloaddition

i

To look at this reaction in detail, we need to first look at the basics.

To this end; cis butadiene was created in GaussView.

This molecule was potimized using the AM1 semi-emperical orbital method, so that the symmetry of the HOMO and LUMO could be determined.

However, there was some problem with GauusView, and the HOMO and LUMO MOs could not be visualised. Therefore, cis butadiene was re-optimised using HF/3-21G theory.

When this result returned, the error was evident; the input molecule was lacking hydrogens.

The CORRECT cis butadiene was constructed in ChemBio 3D, MM2 optimised, and then inported into GaussView. The molecule was then optimised using semi-emperical AM1 thory.

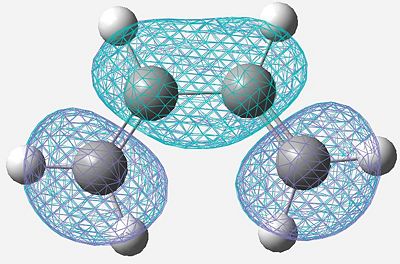
The MOs were visualised and analysed:

MOs of cis butadiene

	Image (1)	Image (2)	Symmetry
LUMO		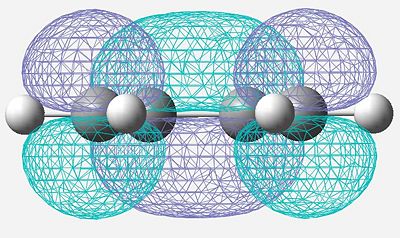	Symmetric
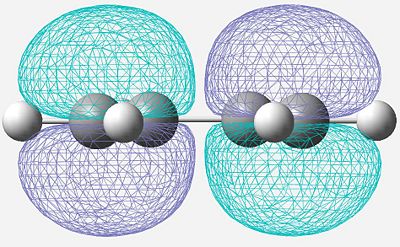
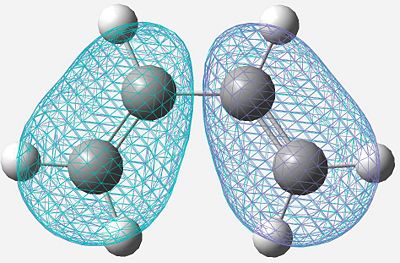
HOMO			Anti-Symmetric

(click to enlarge)

Although not specifically drawn, the plane through which all of these symmetries (and all later symmetyries) are compared; passes vertically down through the center of the molecule (in this case, bisecting the C-C single bond). basically, this plane (in all cases) is the only real way to compare the symmetry of the MOs, the other plane (through the bonds of the molacule horizontally) are not applicable in the later context of the diels alder reaction, as the ethylene/maleic anhydride both approch at angles to the principal bond.

ii

For the prototype reaction, many different methods were attempted, but none of them seemed to work.

First, the two reactants were arranged in an arrangement where the inter molecular C-C distance was set to approximatly 2.2A (what i thought was an appropriate guess), and the intermoleculal C=C C distance was set to approximatly 120°.

This structure was then minimised to TS (Berny), using the HF/3-21G level theory, with the force constants calculated once. The calculation was also appended with the Opt=NoEigen keyword. However, when these calculations returned, there was not one imaginary vibration but 4 present.

When these were analysed, none represented the appropriate "bonding" vibration, but seemed instead to be various vibrations of parts of the transiton vibration and/or vibrations in the plane perpendicular to the expected bond formation.

Since this failed, the molecule was resubmitted with a variation on the frozen coordinate method. Since it is known that the dihedral angle of the cis butadiene remains very close to 0°, this angle was frozen to between 0 and 5° and the intermolecular C C distances were frozen to 2.2A. The structure was run (sucessfully) to a minimum, and then sumbitted for TS (Berny) with the inter molecular carbon carbon "bonds" set to "derivate" instead of "frozen coordinate"

However, this method also ended in faliure, fine would not run to completion stating that the molecules were too constrained.

Therefore, two extensions of this method were attempted; the first method was to take the minimised file and to remove the inter molecular C-C "bond" dinstances freezing, and to only freeze the dihedral angle. This file was then run to a minimum. However, once the results were viewed, the calulation had clearly failed, the C=C of the ethylene had coordinated over only one of the butadiene double bonds, and the transition vibration seemed to show a propane being being formed off one of the terminal butadiede C=C bonds.

The second extension was to unfreeze the bond and leave the inter molecular C-C distances set to 2.2A. However, when this was minimised to a minimum, the butadiene was distorted away form it's dihedral angle of 0, and one of the terminal C=C bond approched the ethylene from each side.

When this all failed, then a break of an hour ensued.

Once themethosds had been reread, a more simpler frozen coordinate method was attempted.

This time, ONLY the inter molecular C-C distances were set to 2.2A and the structure was run to a minimum.

The product of this minimisation looked promising, and so the inter molecular C-C "bonds" were set to "derivate" from "frozen coordinate". This molecule was then optimised using HF/3-21G theory, to a minimum, with force constant calculated once, with a frequency analysis.

The result was this:

jm906Diels_alder_transiitn_vibration

(vibration recorded at -819.4cm^-1

Clearly, this method has worked, and the correct transition vibration has come out of the calculations. The MOs were then analysed;

MOs of cis butadiene and ethylene

	Image (1)	Image (2)	Symmetry
LUMO		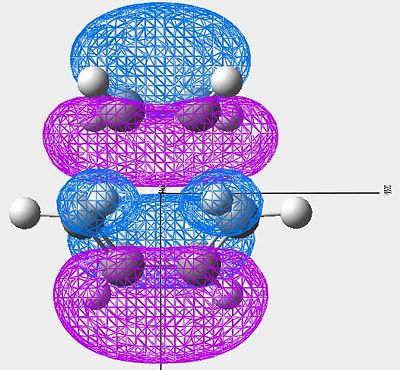	Symmetric
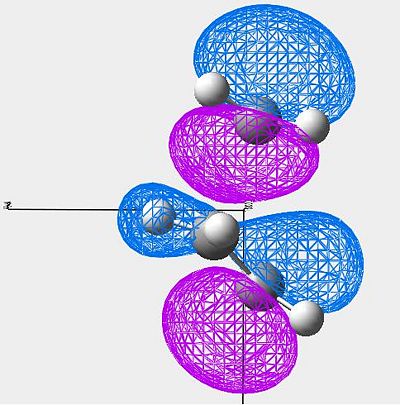
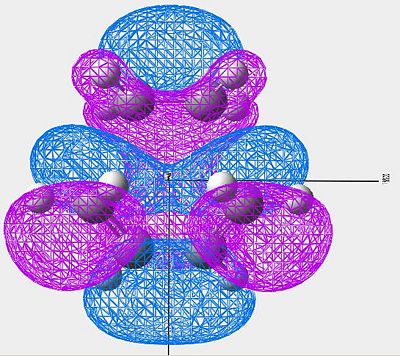
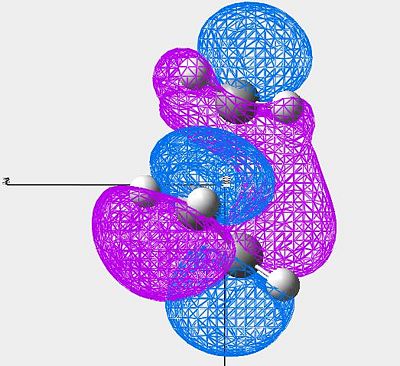
HOMO			Symmetric

(click to enlarge)

Both of these orbitals are symmetric with respect to the central plane.

iii

Now the regio selectivity of the diels alder reaction needs to be investigated. To do this, cyclohexa-1,3-diene and maleic anhydride were both constructed (seperatly) in ChemBio 3D, and MM2 optimisations were run.

These molecules were then combined into GussView, and arranged in a similar fasion to the Diels Alder example (approx 120° intermolecular C=C C angle and 2.2A intermolecular C-C distance). The first example looked at was the exo product, which was arranged as:

jm906Cyclo_hexadiene_and_maleic_anhydride_in_exo

The C-C intermolecular distances were fixed using the frozen coordinate method (to 2.2A) and the structure was optimised, to a minimum ,using HF/3-21G theory.

This minimised structure was then imported back into GaussView, and the previous frozen "bonds" were set to "derivate" (instead of "freeze coordinates"). The structure was then optimised (using HF/3-21G theory) to TS (Berny), with a frequency calculation.

The result of this was one imaginary frequency at -757.9 cm^-1:

jm906Cyclo_hexane_transitin_state_vibrtion_exo

(vibration recorded at -757.9cm^-1)

This is clearly the correct vibration fot the transition state which produces the exo product.

Next, the endo product was explored. The method for this was identical to above, except the starting geometry had the maleic anhydride attacking at a slightly different angle:

jm906Cyclo_hexadiene_and_maleic_anhydride_in_endo

Here; the maleic anhydride is attacking form the lower face of the cyclohexadiene. After analysis, an imaginary frequency (at -722.8cm^-1) was obtained:

jm906Cyclo_hexane_transition_vibration_endo

(vibration recorded at -722.8cm^-1)

Clearly, the correct transition state for the endo product has also been found.

Comparing the data found, we find the following:

	Endo Product Transition State	Exo Product Transition State
Geometry
Energy (Hartrees)	-605.61079791	-605.60535437

From the energies, we have confirmed that the exo product is higher in energy, and that the endo product is thermodynamically more favoured.

Secondary Orbital Overlap (SOO) is defined as the positive overlap of a nonactive frame in the frontier molecular orbitals of a pericyclic reaction .

To observe this, the MOs must be visualised:

	HOMO of Endo Product	LUMO of Endo Product
Image 1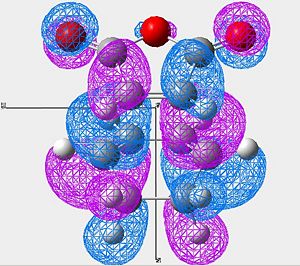
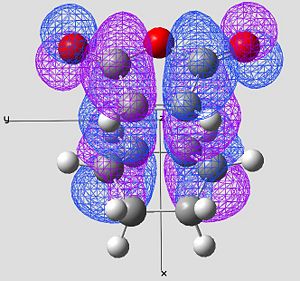
Image 2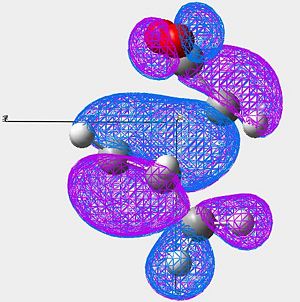
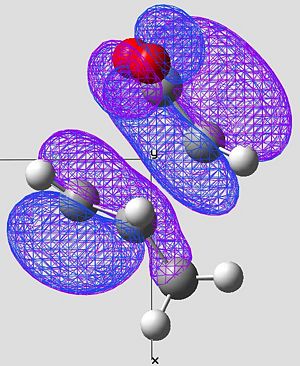
Symmetry	Anti-Symmetric	Anti-Symmetric

In the endo product (looking mainly at image 2) we see strong overlap between the HOMO of the cyclo hexadiene and the LUMO of the Maleic anhydride.

Looking at the very center of the transition state (between the two molecules) there is a vary large "blue" orbital on the HOMO of the cyclo hexadiene. This is on the same side of the transition state as the smaller "blue" orbital on the LUMO of the maleic anhydride. These orbitals are therefore in phase and will constructivly overlap (SOO). The reaction is allowed

	HOMO of Exo Product	LUMO of Exo Product
Image 1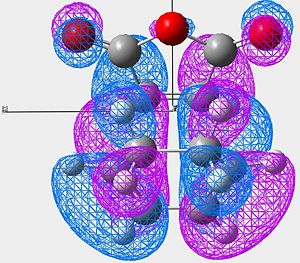
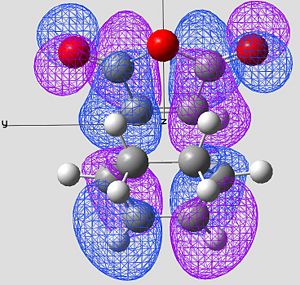
Image 2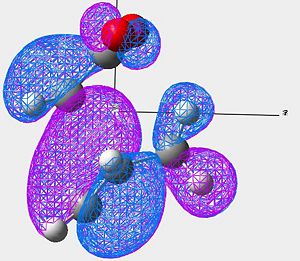
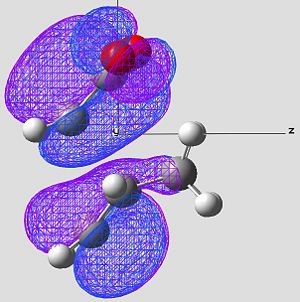
Symmetry	Anti-Symmetric	Anti-Symmetric

In the case of the exo, the large cyclo hexadiene HOMO orbital and the maleic anhydride LUMO orbital are out of phase. Therefore this overlap is not disfavourable to the reaction and therefore raises the energy of the molecule. This reaction is forbidden.

Since the Exo is primarilly effected by steric effects and the endo is primarilly effected by the SOO effect; it is clear that the SOO effect applies a greater stabilisation to the transition state than steric effects (as the endo ts is lower in energy than the exo).