MRD:evs316

Molecular Reaction Dynamics

Exercise 1: H + H2 system

The Gradient of the Potential Energy Surface

Question 1: What value do the different components of the gradient of the potential energy surface have at a minimum and at a transition structure? Briefly explain how minima and transition structures can be distinguished using the curvature of the potential energy surface.

The different components of the gradient of the potential energy surface at a minimum and at the transition state all have a value of zero.

∂V(ri)/∂ri=0

As the transition state is at a maximum on the minimum energy path, the gradient of the potential energy surface decreases either side of the transition state. Second derivatives can be used to differentiate between minima and transition states. For minima, all components of the gradient will have a second derivative that is greater than zero along all directions. The second derivative of transition states for one component will be less than zero (along the reaction coordinate) and for the other components it will be greater than zero. The transition state is called a saddle point - it is a maximum along the reaction coordinate but a minimum in all other directions.

Transition State Position

Question 2: Report your best estimate of the transition state position (r_ts) and explain your reasoning illustrating it with a “Internuclear Distances vs Time” plot for a relevant trajectory.

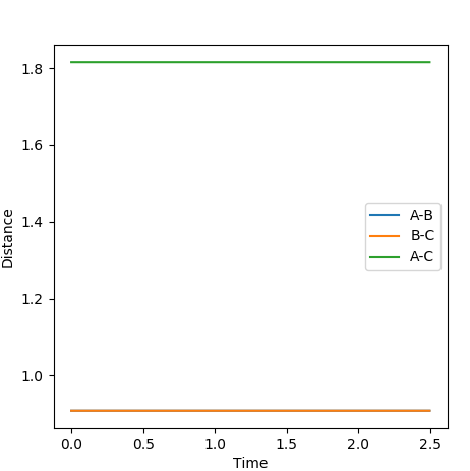
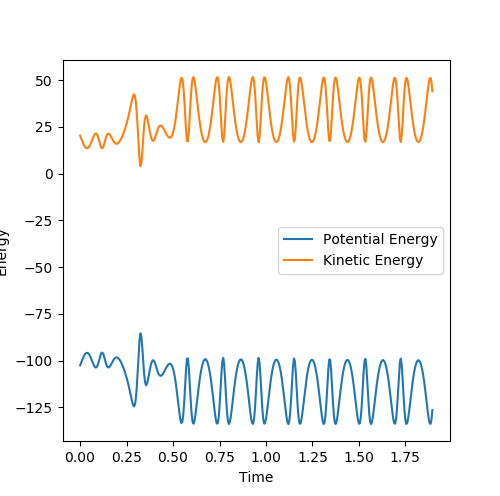
The transition state position, r_ts, is at 0.9078 Angstroms. A plot of internuclear distance vs time at the transition state position shows a constant internuclear separation between all the atoms present. It can thus be inferred that no bonds are made or broken at the transition state position.

The Internuclear Distance vs Time plot at the transition state position is shown above, where p_AB=0 and p_BC=0.

Minimum Energy Path

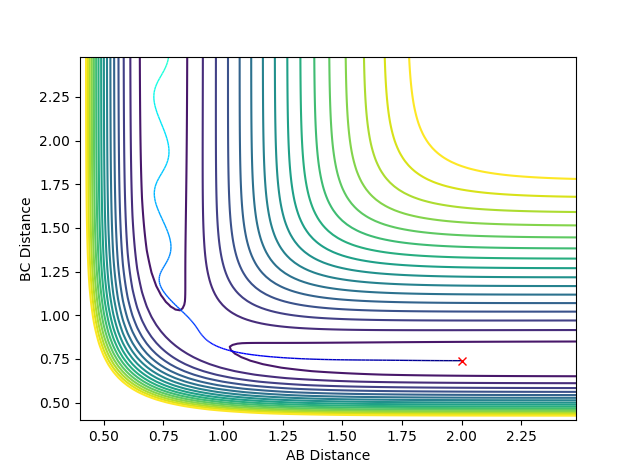
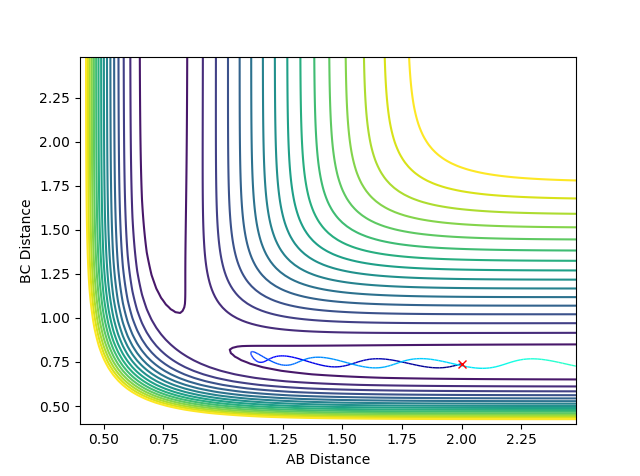
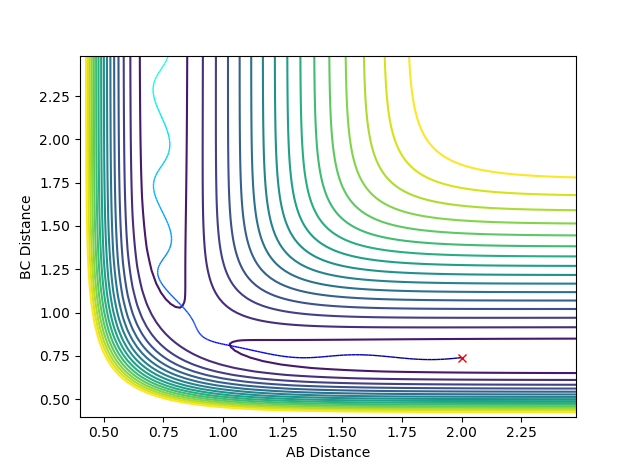
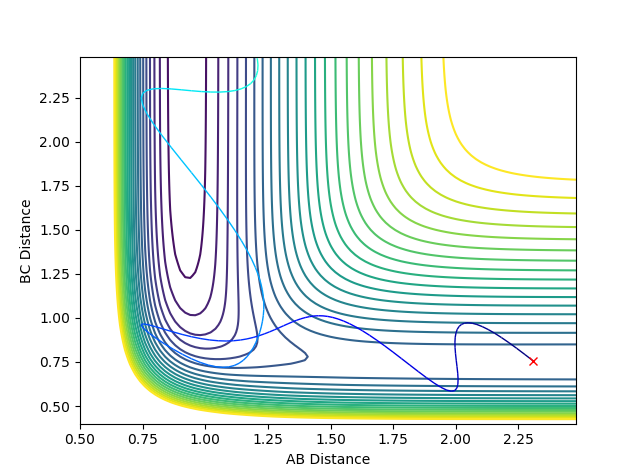
Question 3: Comment on how the mep and the trajectory you just calculated differ.

Using the MEP calculation type, the trajectory can be seen to follow from the transition state down to the valley floor where H_A-H_B and H_C exist. Using the Dynamics calculation type, the trajectory of the minimum energy path falls to the valley floor from the transition state, but H_C continues to move away from H_A-H_B so that the BC distance increases. There are oscillations in the Dynamics trajectory, whereas there are no oscillations in that of the MEP trajectory. These oscillations are due to changes in the potential energy of the hydrogen molecule due to vibrations. Oscillations are deviations from the equilibrium position which lead to an increase in energy. In the MEP calculation, the velocity is reset to zero in each time step and the minimum energy path is always taken. Therefore the MEP trajectory involves no oscillations.

Jas213 (talk) 00:19, 14 May 2018 (BST) A plot of a dynamic and a MEP trajectory would have illustrated this nicely.

Reactive and Unreactive Trajectories

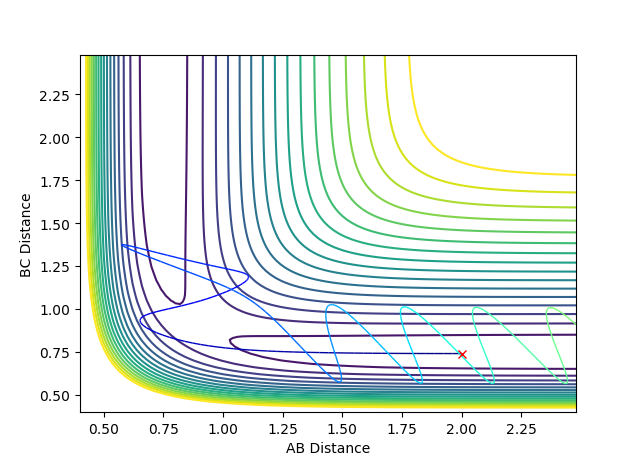
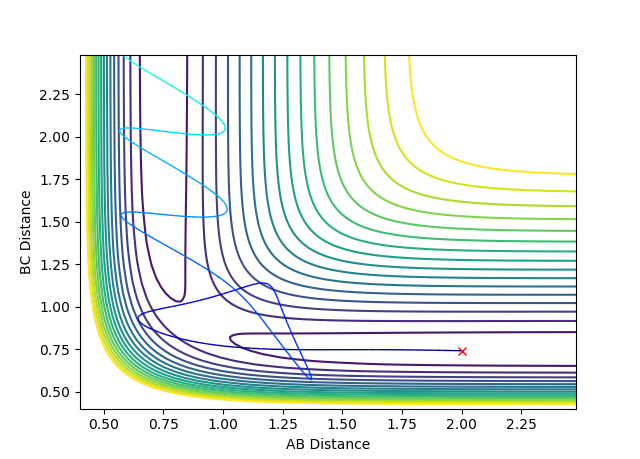
Question 4: Complete the table by adding a column with the total energy, and another column reporting if the trajectory is reactive or unreactive. For each set of initial conditions, provide a plot of the trajectory and a small description for what happens along the trajectory.

If the trajectory goes from the reactant channel to the product channel, the trajectory is taken to be reactive. The trajectories were run for the initial positions r₁ = 0.74 and r₂ = 2.0 with the differing momenta combinations.

p1	p2	Total Energy	Reactive or Unreactive?	Plot	Description of trajectory
-1.25	-2.5	-99.018	Reactive		A approaches B-C when it is not vibrating. The product, A-B, vibrates once formed.
-1.5	-2.0	-100.456	Unreactive		The trajectory does not enter the product channel. The barrier is too great.
-1.5	-2.5	-98.956	Reactive		The trajectory does enter the reaction channel. Oscillations are seen in both reactants and products.
-2.5	-5.0	-84.956	Unreactive		The system crosses the transition state and the HA-HB bond forms before the system reverts to the reactants. The energy is not great enough to enter the product channel. This is known as a barrier recrossing.
-2.5	-5.2	-83.416	Reactive		The product vibrates with a lot of energy.

Jas213 (talk) 00:05, 14 May 2018 (BST) Good that you stated the initial conditions. The last case is also an example of recrossing. An overall concluding comment of what you learned from this table would have been expected. Good that you describe the oscillations, would have been ever nicer if you had related them back to the kinetic energy and the applied momenta.

Transition State Theory

Question 5: State what are the main assumptions of Transition State Theory. Given the results you have obtained, how will Transition State Theory predictions for reaction rate values compare with experimental values?

The Born-Oppenheimer approximation is invoked. Reactants are assumed to follow the Maxwell-Boltzmann Distribution.

The main assumptions of Transition State Theory are:

1. Once the molecular system has crossed the transition state in the direction of the products, the reactants cannot be reformed.

2. Motion along the reaction coordinate can be treated classically as a translation and separated from other motions for the transition state.

3. Maxwell-Boltzmann laws determine the distribution among their states of the transition states that are becoming products, even in the absence of an equilibrium between reactants and products.

Systems with light atoms, for example hydrogen, are often exceptions to these assumptions due to the increased importance of quantum mechanics in these systems. The barrier re-crossing in the previous example is an instance of the first of the assumptions being broken.

EXERCISE 2: F - H - H system

PES Inspection

Question 6: Classify the F + H_{2 and H + HF reactions according to their energetics (endothermic or exothermic). How does this relate to the bond strength of the chemical species involved?}

The F + H₂ reaction is exothermic. It has a smaller barrier than that in the H + H₂ system. The potential energy drops steeply after the barrier. The transition state is early and thus resembles the reactants (according to Hammond's postulate). This is an example of an attractive potential. The H + H-F reaction is endothermic. This can be understood using bond enthalpies and the fact that bond formation is exothermic whilst bond breaking is endothermic. The H-F bond is stronger than the H-H bond. More energy is released when the H-F bond (565 kJ/mol) is formed than is required to break the H-H bond (432 kJ/mol).

Question 7: Locate the approximate position of the transition state.

In the F + H₂ system, the F-H distance is approx. 1.81 Angstroms and the H-H distance is approx. 0.746 Angstroms.

Jas213 (talk) 00:19, 14 May 2018 (BST) How did you find this TS?

In the HF + H system, the transition state occurs at the same coordinates. The F-H distance is approx. 1.81 Angstroms and the H-H distance is approx. 0.746 Angstroms.

Jas213 (talk) 00:19, 14 May 2018 (BST) The transition state is not just approximately the same, it is the same PES, just the other way round.

Question 8: Report the activation energy for both reactions.

The activation energy can be calculated using the MEP calculation time and a high number of steps. The activation energy for the reaction is the energy difference between the transition state and the reactants. The transition state energy was found to be -103.752 kJ/mol. The energy of the reactants with the F + H₂ system was found to be -103.991 kJ/mol. Therefore the activation energy for the F + H₂ system is 0.239 kJ/mol. The energy of the reactants with the HF + H system was found to be -133.837 kJ/mol. Therefore the activation energy for the HF + H system is 30.085 kJ/mol.

Reaction Dynamics

Question 9: In light of the fact that energy is conserved, discuss the mechanism of release of the reaction energy. How could this be confirmed experimentally?

The conditions used were:

F-H distance: 2.31

H-H distance: 0.755

F-H momentum: -6.8

H-H momentum: -1

The F + H₂ reaction is exothermic and thus results in a release of energy. That release of energy causes the F-H bond which is formed to vibrate with a greater amplitude. The law of conservation of energy states that energy cannot be created nor destroyed. The total energy of an isolated system remains constant. Energy can only be transformed from one form into another. Therefore, as the potential energy decreases, the kinetic energy increases. Repulsive potentials predominantly transfer energy to translational modes, whereas attractive potentials transfer it to vibrational modes.

Enthalpy changes can be confirmed experimentally using calorimetry. However, calorimetry will not distinguish whether the energy was transferred to vibrational or translational modes. Determining an altered translational energy can be achieved by measuring pressure changes. The more translational energy the molecule has, the greater the pressure of the system will become. IR spectroscopy can be used to determine changes in vibrational energy. Vibrationally excited molecules will emit IR radiation as they relax to the ground state.

Question 10: Discuss how the distribution of energy between different modes (translation and vibration) affect the efficiency of the reaction, and how this is influenced by the position of the transition state.

Polanyi's rules state that vibrational energy is more efficient than translational energy in activating a reaction with a late barrier. The reverse is true for an early-barrier reaction.

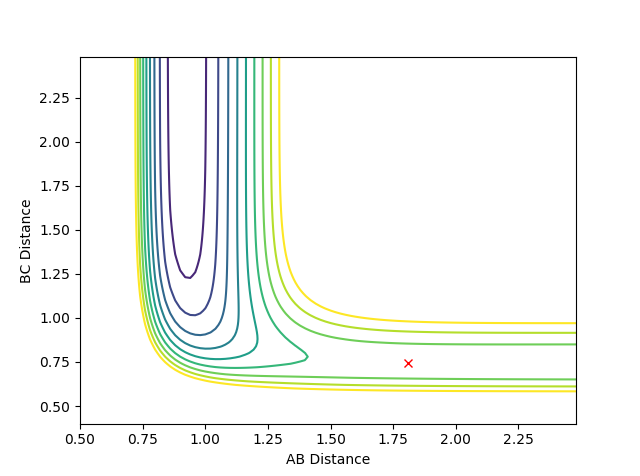
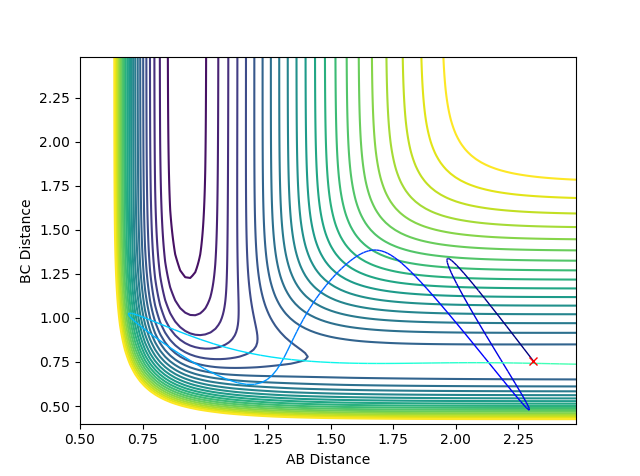
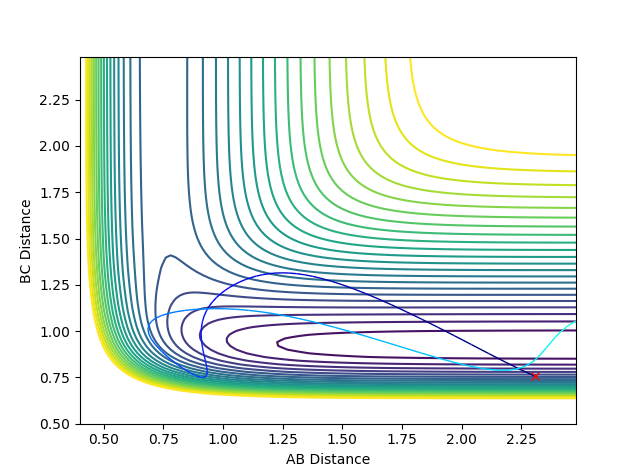
For the F + H₂ reaction - which is exothermic and has an early transition state - the barrier (transition state) occurs in the early stages of the reaction. Therefore, according to Polanyi's rules, the translational energy is more efficient in activating the reaction. A reactive reaction can be achieved by an increase in the translational energy above the vibrational energy. The following plots indicate Polanyi's rules.

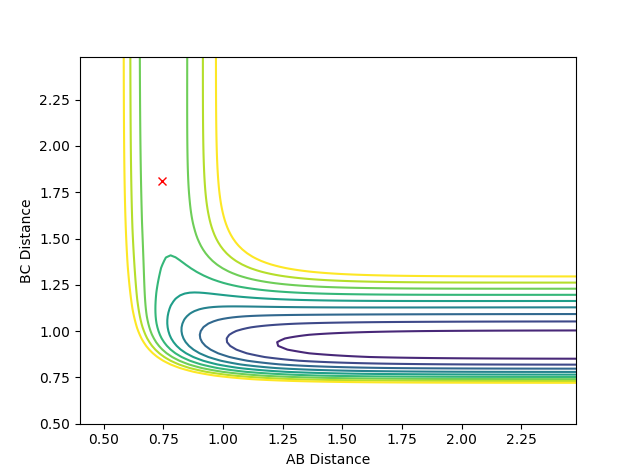
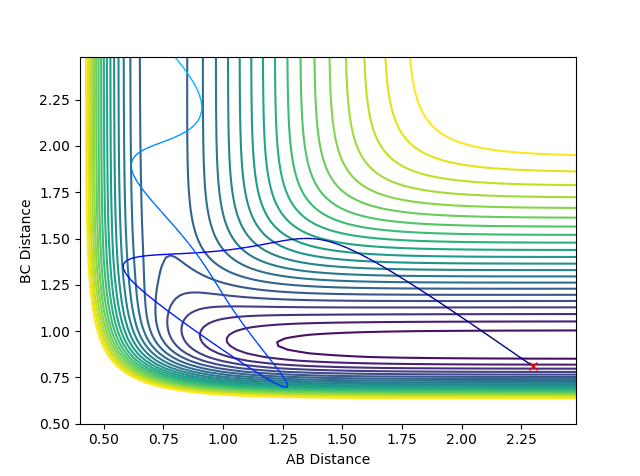
For the HF + H reaction - which is endothermic and has a late transition state - the barrier (transition state) occurs in the late stages of the reaction. Therefore, according to Polanyi's rules, the vibrational energy is more efficient in activating the reaction. A reactive reaction can be achieved by an increase in the vibrational energy above the translational energy. The following plots indicate Polanyi's rules, where p₁ is vibrational energy and p₂ is translational energy. The F-H and H-H distances used were as above (2.31 and 0.755 Angstroms, respectively).

Reaction	p1	p2	Plot	Description
F + H2	-5.5	1		This system has low vibrational energy and high translational energy. The trajectory is reactive, and thus the system obeys Polanyi's rules for an exothermic system.
F + H2	-1	6.5		This system has high vibrational energy and low translational energy. The trajectory is not reactive, and thus the system obeys Polanyi's rules for an exothermic system.
HF + H	-2	8.5		This system has high vibrational energy and low translational energy. The trajectory is reactive, and thus the system obeys Polanyi's rules for an endothermic system.
HF + H	-5.0	1		This system has low vibrational energy and high translational energy. The trajectory is not reactive, and thus the system obeys Polanyi's rules for an endothermic system.

Jas213 (talk) 00:19, 14 May 2018 (BST) Good that you mentioned Polanyi's rules and discussed them with some examples. Also I like the clear description above the plots of momenta and distances applied. Next time, try to step aside from the question and answer style of your report and make it more like a research report.

References